第16章 熱力学

図16.1 | 間欠泉は自然における熱力学的原理を劇的に示しています。間欠泉の深い地下水脈内にある水は、高圧下にあり、マグマによって高温に加熱されています。地表近くのひとまとまりの水が沸点に達して排出されるとき、その結果として生じる圧力の低下は、大量の水の瞬間沸騰を引き起こし、蒸気と水を力強く射出し、印象的な噴出を引き起こします。(credit: modification of work by Yellowstone National Park)
この章の概要
16.1 自発性
16.2 エントロピー
16.3 熱力学の第二法則と第三法則
16.4 自由エネルギー
はじめに
化学の多くの能力の中には、ある過程が特定の条件下で発生するかどうかを予測する能力があります。熱力学は、化学的・物理的過程に関連するエネルギーと仕事の間の関係性を研究する学問であり、この予測能力を提供します。この教科書の以前の章では、化学反応や相転移に伴う熱流に関係する熱力学の重要な側面である熱化学のさまざまな応用について記述してきました。この章では、与えられた一組の条件下での化学的または物理的変化を予測することを可能にするものを含む、追加の熱力学的概念を導入します。
16.1 自発性
この節が終わるまでに、あなたは次のことができるようになります:
•自発過程と非自発過程を区別する
•ある自発過程に伴う物質とエネルギーの分散について記述する
プロセスは、与えられた一組の条件下で一方向に発生する自然な傾向を持っています。水は自然に下に向かって流れますが、上に向かって流れるためにはポンプの使用などの外部の介入を必要とします。地球の大気中にさらされた鉄は腐食しますが、意図的な化学処理をしなければ錆は鉄に変わりません。自発過程とは、ある条件下で自然に起こるプロセスのことです。一方、非自発過程は、外部の源からのエネルギーの継続的な投入によって「駆動」されなければ起こりません。ある特定の一組の条件下で一方向に自発的に起こるプロセスは、逆方向には非自発的です。たとえば、室温と典型的な大気圧では、氷は自発的に溶けますが、水は自発的には凍りません。
プロセスの自発性は、プロセスの速度とは相関がありません。自発的な変化は、実質的に一瞬で起こるほど急速な場合もあれば、実用的な時間の間隔では観察することができないほど遅い場合もあります。この概念を説明するために、放射性同位体の崩壊を考えてみましょう(このトピックについては、核化学の章でより徹底的に扱います)。放射性崩壊とは、定義上、不安定な同位体の原子核がより安定な原子核に変換される際に放射線を放出する自発過程です。すべての崩壊過程は自発的に起こりますが、さまざまな同位体の崩壊速度は大きく異なります。テクネチウム-99mは、医療用画像研究でよく使われる放射性同位体であり、比較的急速に崩壊し、半減期は約6時間です。ウラン-238はウランの中で最も豊富にある同位体であり、その崩壊は非常にゆっくりと起こり、半減期は40億年以上です(図16.2)。
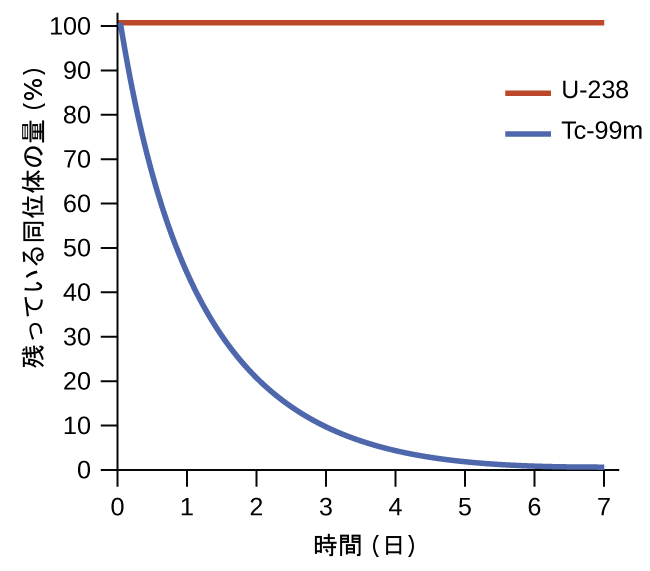
図16.2 | U-238もTc-99mも自発的な放射性崩壊を起こしますが、その速度は全く異なります。1週間の間に、Tc-99mの試料は実質的にすべてが崩壊していますが、U-238の試料はまったく崩壊していないでしょう。
別の例として、ダイヤモンドから黒鉛への変換を考えてみましょう (図16.3)。
\[ {\rm C\ (s、ダイヤモンド) ⟶ C\ (s、黒鉛)}\\ \]
炭素の相図を見ると、通常の大気圧下では黒鉛がこの元素の安定した形態であるのに対し、地質学的形成時のような非常に高い圧力下ではダイヤモンドが安定した同素体であることがわかります。この章の最後の節で説明するような熱力学計算によると、常圧でのダイヤモンドから黒鉛への変換は自発的に起こることが示されますが、ダイヤモンドはこのような条件下であっても存在し、残り続けていることが観察されています。そのプロセスは典型的な通常の条件下で自発的に起こるとはいえ、その速度は極端に遅く、実用的な目的のためにはダイヤモンドは実際には「永遠に」存在しているのです。このような状況は、プロセスの熱力学的側面と反応速度論的側面とを区別することの重要性を強調しています。この特定のケースの場合、通常の条件下ではダイヤモンドは熱力学的には不安定ですが、反応速度論的には安定していると言われます。
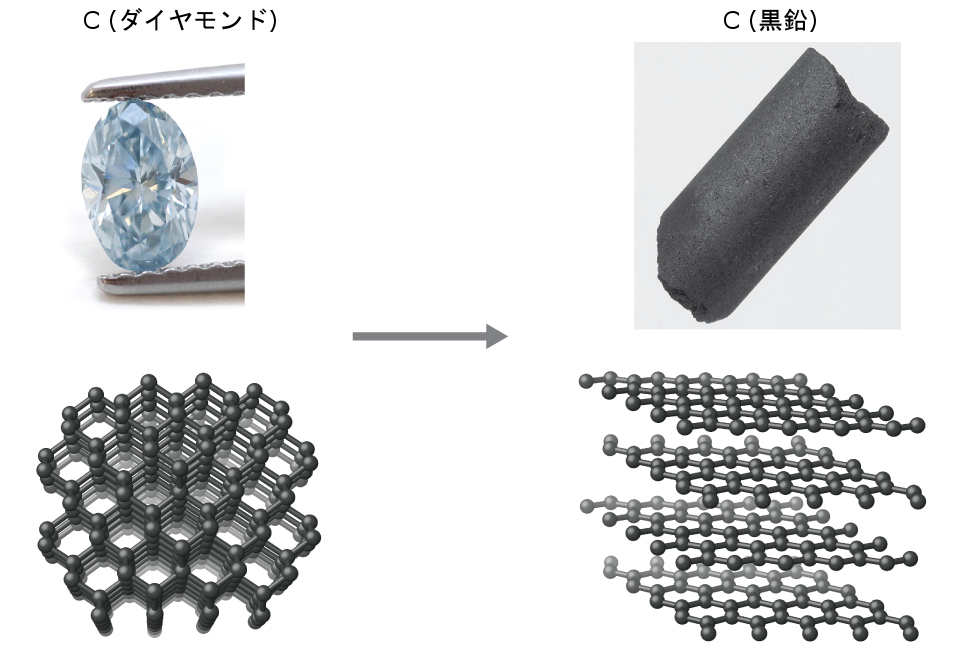
図16.3 | ダイヤモンドの同素体から黒鉛の同素体へという炭素の変換は、常圧では自発的に起こりますが、低温から中程度の温度ではその速度は測定できないほど遅いです。このプロセスは黒鉛化として知られており、その速度は1000~2000Kの範囲の温度においては容易に測定可能な値まで増加させることができます。(credit “diamond” photo: modification of work by “Fancy Diamonds”/Flickr; credit “graphite” photo: modificaton of work by images-of-elements.com/carbon.php)
物質とエネルギーの分散
熱力学的概念の議論を自発性の予測という目的へ向けて拡張するために、閉じた弁で接続された2つのフラスコからなる孤立した系を考えてみましょう。最初は片方のフラスコに理想気体が入っていて、もう片方のフラスコは空(P = 0)です(図16.4)。弁を開くと気体は自発的に膨張して両方のフラスコを等しく満たすようになります。熱化学の章から圧力-体積仕事の定義を思い出すと、真空中の圧力はゼロなので仕事は何もなされていないことに注意してください。
\[ w = −PΔV = 0\ (真空中でP = 0)\\ \]
また、系が孤立しているので、熱が周囲とやり取りされていないことにも注意してください(q = 0)。熱力学の第一法則は、このプロセスの結果として系の内部エネルギーに変化がないことを裏付けます。
\[ ΔU= q + w = 0 + 0 = 0\\ \]
したがって、このプロセスの自発性は、プロセスに伴うエネルギーの変化の結果ではありません。そうではなくて、気体が膨張できるようになった時に生じる、より大きく、より均一な物質の分散が原動力となっているようです。当初、この系は、物質を含む1つのフラスコと何も含まない別のフラスコで構成されていました。自発的な膨張が起こった後、物質はより広く(元の体積の2倍を占めるように)、より均一に(それぞれのフラスコに等しい量で存在するように)、分配されました。

図16.4 | 孤立した系は、理想気体の入った1つ目のフラスコと、真空である2つ目のフラスコを閉じた弁で接続することにより構成されています。弁が開かれると、気体は自発的にフラスコの間に均等に分布するようになります。
ここで、温度の異なる2つの物体を考えてみましょう:物体 X の温度は TX、物体 Y の温度は TYで、TX > TY とします(図16.5)。これらの物体が接触すると、高温の物体(X)から低温の物体(Y)に熱が自発的に流れます。これはXによる熱エネルギーの損失とYによる熱エネルギーの獲得に対応します。
\[ q_{\rm X} < 0\ および\ q_{\rm Y} = −q_{\rm X} > 0\\ \]
この2つの物体の系の観点から見ると、熱エネルギーの正味の増減はなく、むしろ利用可能な熱エネルギーが2つの物体間で再分配されています。この自発過程の結果、エネルギーの分散は、より均一になります。

図16.5 | 温度の異なる2つの物体が接触すると、熱い方から冷たい方に熱が自発的に流れます。
ここで記述した2つのプロセスで示されているように、プロセスの自発性を決定する重要な要素は、それが物質および/またはエネルギーの分散や分布をどの程度変化させるかということです。それぞれのケースでは、自発過程が起こって、物質またはエネルギーのより均一な分布をもたらしました。
例題16.1 自発過程の間での物質の再分配
以下のような自発過程が起こったとき、物質がどのように再分配されるかを記述してください:
(a)固体が昇華する。
(b)気体が凝縮する。
(c)コップ一杯の水に食品着色料を一滴加えると、均一な色の溶液ができる。
解法

図16.6 | (credit a: modification of work by Jenny Downing; credit b: modification of work by “Fuzzy Gerdes”/Flickr; credit c: modification of work by Paul A. Flowers)
(a)昇華とは、固体(比較的密度が高い)から気体(はるかに密度が低い)への変換です。このプロセスでは、固体から気体への変換後に分子がより大きな体積を占めることになるため、物質の分散がより大きくなります。
(b)凝縮とは、気体(比較的密度が低い)から液体(はるかに密度が高い)への変換です。このプロセスでは、気体から液体への変換後に分子がより小さな体積を占めることになるため、物質の分散がより小さくなります。
(c)問題となっているプロセスは拡散です。このプロセスでは、物質のより均一な分散が得られます。なぜなら、この系の初期状態は異なる染料濃度の2つの領域(染料の滴では高く、水ではゼロ)を含み、系の最終状態は全体にわたって単一の染料濃度を含むからです。
学習内容の確認
室温のスプーンをホットコーヒーに入れたとき、エネルギーがどのように再分配されるかを記述してください。
解答:熱は、熱い方の物体(コーヒー)から冷たい方の物体(スプーン)に自発的に流れ、スプーンが温まり、コーヒーが冷めることで、熱エネルギーのより均一な分布をもたらします。
16.2 エントロピー
この節が終わるまでに、あなたは次のことができるようになります:
•エントロピーを定義する
•エントロピーと微視的状態の数との間の関係性を説明する
•化学的・物理的プロセスのエントロピー変化の符号を予測する
1824年、28歳のニコラ・レオナール・サディ・カルノー(図16.7)は、蒸気熱機関の効率に関する広範な研究結果を発表しました。後にルドルフ・クラウジウスがカルノーの発見を再検討した結果、あるプロセスに伴う自発的な熱流と、そのプロセスが行われる温度とを関連付ける新しい熱力学的性質が導入されました。この新しい性質は、可逆熱(q可逆)とケルビン温度(T)の比として表現されました。熱力学では、可逆過程とは、非常にゆっくりとした速度で起こるために、常に平衡にあり、何らかの条件のごく小さな変化によってその方向を変えることができる(「反転」させることができる)ようなプロセスのことを指します。可逆過程の考え方は、さまざまな熱力学的な概念の展開を支えるために必要な形式的なものであることに注意してください。実際のプロセスで真に可逆的なものはなく、それらはむしろ不可逆的なものとして分類されます。

図16.7 | (a)ニコラ・レオナール・サディ・カルノーの蒸気動力機械の研究と、(b)ルドルフ・クラウジウスが後にそれらの発見を研究したことにより、自発的な熱流過程に関する画期的な発見がなされました。
この新しい量は、他の熱力学的性質と同様に状態関数であるため、その変化は系の初期状態と最終状態にのみ依存します。1865年、クラウジウスはこの性質をエントロピー(S)と名付け、任意のプロセスについてのその変化を以下のように定義しました:
\[ ΔS =\frac{q_{可逆}}{T}\\ \]
実際の不可逆過程についてのエントロピーの変化は、同じ初期状態と最終状態を含む理論的な可逆過程についてのエントロピーの変化と等しいです。
エントロピーと微視的状態
カルノーとクラウジウスの研究に続いて、ルートヴィッヒ・ボルツマンは、ある系のエントロピーと、その系について可能な微視的状態(W)の数とを関連付けるような、分子スケールの統計学的モデルを開発しました。微視的状態とは、系を構成する原子や分子のすべての位置とエネルギーについての特定の構成のことです。ある系のエントロピーと可能な微視的状態の数との関係は以下の通りです。
\[ S = k \ln W\\ \]
ここで k はボルツマン定数であり、1.38 × 10⁻²³J/K です。
他の状態関数と同様に、あるプロセスのエントロピーの変化とは、その最終値(Sf)と初期値(Si)の間の差です:
\[ ΔS = S_{\rm f} − S_{\rm i} = k \ln W_{\rm f} − k \ln W_{\rm i} = k \ln \frac{W_{\rm f}}{W_{\rm i}}\\ \]
微視的状態の数の増加を伴うプロセス(Wf > Wi)では、系のエントロピーが増加し、ΔS > 0となります。逆に、微視的状態の数を減少させるプロセス(Wf < Wi)では、系のエントロピーが減少し、ΔS < 0となります。このエントロピーについての分子スケールの解釈は、次の段落で説明するようなプロセスが発生する確率へのつながりを提供してくれます。
N個の粒子がn個の箱に分配される系という一般的なケースを考えてみましょう。このような系で可能な微視的状態の数はnᴺです。たとえば、4 つの粒子を 2 つの箱に分配すると、図16.8に示されているように、2⁴ = 16 の異なる微視的状態が生じます。等価な粒子の配置(個々の粒子の同一性を考慮せずに)を持つ微視的状態はグループとしてまとめられ、それは分布と呼ばれます。ある系が所与の分布の中にその構成要素を持つようにして存在する確率は、その分布内の微視的状態の数に比例します。エントロピーは微視的状態の数に対して対数的に増加するので、 最も確率の高い分布は最大のエントロピーを持つ分布となります。
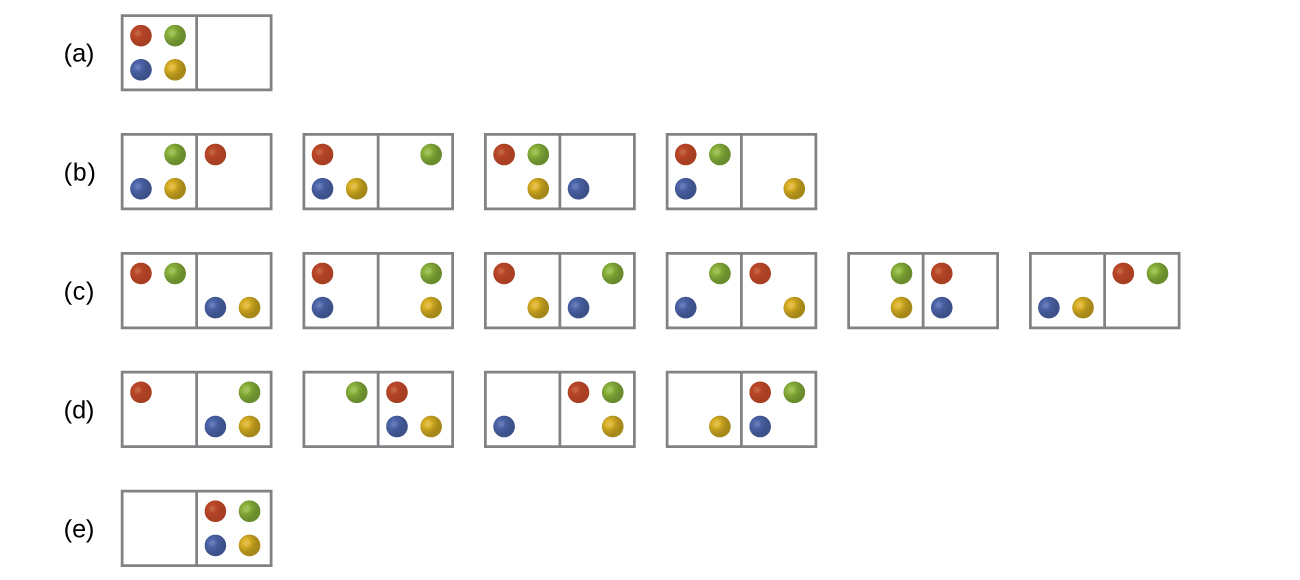
図16.8 | 2つの箱に4つの粒子を配置したときの16個の微視的状態が示されています。この微視的状態は、それぞれの箱の中の粒子の数に基づいて、5つの分布(a)、(b)、(c)、(d)、(e)にまとめられています。
この系では、最も確率の高い構成は、粒子が2つの箱の間で均等に分配されている分布(c)に関連する6つの微視的状態のうちの1つの構成、すなわち、それぞれの箱に2つの粒子が存在するような構成です。系がこの構成にある確率は6/16、つまり3/8です。この系の最も低い確率の構成は、4つの粒子がすべて1つの箱に入っているもので、分布(a)と分布(e)に対応し、それぞれの確率は1/16です。全ての粒子が1つの箱(左側の箱か右側の箱)に入っている確率は、(1/16) + (1/16) = 2/16、つまり1/8です。
系にさらに多くの粒子を追加すると、可能な微視的状態の数は指数関数的に増加します(2ᴺ)。巨視的な(実験室サイズの)系は、通常では、粒子のモル数(N ~ 10²³)で構成されており、それに対応する微視的状態の数は驚くほど膨大なものになります。しかしながら、系内の粒子の数にかかわらず、それぞれの箱の中にほぼ等しい数の粒子が存在する分布が常に最も可能性の高い構成となります。
このエントロピーについての物質の分散モデルは、しばしば系の無秩序さの観点から定性的に記述されます。この記述では、すべての粒子が1つの箱に入っている微視的状態が最も秩序があり、したがって、最小のエントロピーを持っています。粒子が複数の箱の間でより均等に分配されている微視的状態は、より無秩序で、より大きなエントロピーを持っています。
前述の理想気体が真空中に膨張する様子(図16.4)は、この「箱の中の粒子」モデルの巨視的な例です。この系において、最も可能性の高い分布は、2つのフラスコの間に物質が最も均一に分散または分配されている分布であることが確認できます。最初は、気体分子は2つのフラスコのうちの1つだけに閉じ込められています。フラスコの間の弁を開くと、気体分子が利用できる体積が増え、それに応じてこの系の可能な微視的状態の数が増えます。Wf > Wi であるため、この膨張過程はエントロピーの増加を伴い(ΔS > 0)、自発的なものです。
同様のアプローチを熱の自発的な流れを記述するために使用することができます。図16.9の2つの物体(それぞれが2つの粒子を含みます)と、2つの熱エネルギーの単位(「*」で表されています)からなる系を考えてみましょう。高温の物体は粒子AとBで構成されており、初期には両方のエネルギー単位を含んでいます。低温の物体は粒子CとDで構成されており、初期にはエネルギー単位を持ちません。分布(a)は、系の初期状態(高温の物体に両方のエネルギー単位が含まれています)の3つの微視的状態を示しています。2つのエネルギー単位のうちの1つが移動した場合、結果は4つの微視的状態からなる分布(b)となります。両方のエネルギー単位が移動した場合、結果は3つの微視的状態からなる分布(c)となります。このように、私たちはこの系を合計10個の微視的状態で記述することができます。2つの物体を接触させたときに熱が流れない確率、つまりこの系が分布(a)のままである確率は3/10です。より可能性が高いのは、熱の流れによって他の2つの分布のいずれかがもたらされることであり、その組み合わせの確率は7/10です。最も可能性の高い結果は、熱の流れによって分布(b)で表されるエネルギーの均一な分散がもたらされることであり、この構成の確率は4/10です。このことは、高温の物体と低温の物体を接触させると、自発的な熱流が生じ、最終的に物体の温度が等しくなるという一般的な観察を支持しています。そして、やはりこの自発過程も系のエントロピーの増加によって特徴付けられます。
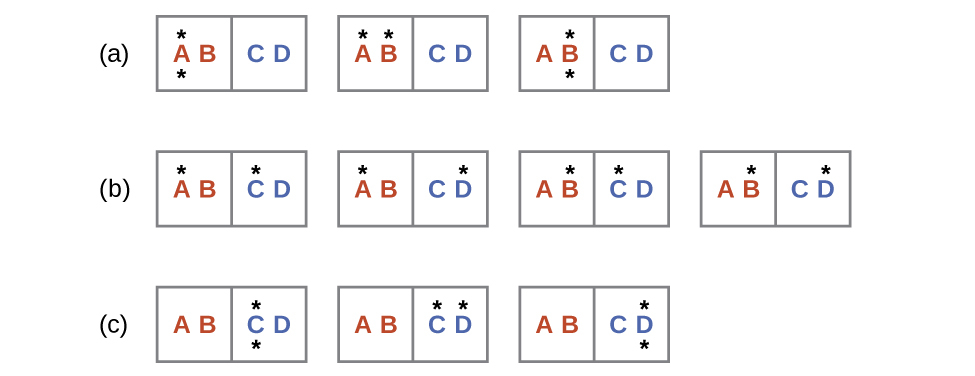
図16.9 | これは、高温の物体から低温の物体への熱の流れを記述した微視的状態モデルを示しています。(a)熱流が発生する前には、粒子AとBからなる物体は両方のエネルギーの単位を有しており、3つの微視的状態からなる分布で表されています。(b)熱流の結果、エネルギーが均等に分散した場合(1つのエネルギー単位が移動した場合)、4つの微視的状態からなる分布が得られます。(c)両方のエネルギー単位が移動した場合、結果として得られる分布は3つの微視的状態を有しています。
例題16.2 ΔSの決定
以下に描かれたプロセスのエントロピーの変化を計算してください。

解法
微視的状態の初期の数は1、最終的な数は6です:
\[ ΔS = k \ln \frac{W_{\rm f}}{W_{\rm i}}= 1.38 × 10^{−23}\ {\rm J/K}× \ln \frac{6}{1}= 2.47 × 10^{−23}\ {\rm J/K}\\ \]
この結果の符号は期待されるものと一致しています。最終状態において可能な微視的状態は、初期状態において可能な微視的状態よりも多いので、エントロピーの変化は正の値になるはずです。
学習内容の確認
図16.9に示される系を考えてみましょう。すべてのエネルギーが高温の物体(AB)から低温の物体(CD)に移動するプロセスでのエントロピーの変化は何ですか?
解答:0 J/K
ΔSの符号を予測する
以前に説明したエントロピー、微視的状態、物質/エネルギーの分散の間の関係性によって、私たちは物質の相対的なエントロピーに関する一般化を行い、化学的・物理的プロセスについてのエントロピー変化の符号を予測することができます。図16.10に示されている相変化を考えてみましょう。固相では、原子や分子はお互いに対してほぼ固定された位置に制限されており、これらの位置の周りでほんのわずかな振動をすることしかできません。系を構成する粒子の位置が本質的に固定されているため、微視的状態の数は比較的少ないです。液相では、原子や分子は互いに比較的近接したままであるにもかかわらず、お互いに自由に動き回ることができます。このように運動の自由度が高くなると、粒子の可能な位置のばらつきが大きくなるため、それに応じて微視的状態の数も固体の場合より多くなります。その結果、S液体 > S固体となり、物質を固体から液体に変換する過程(融解)は、エントロピーが増加する(ΔS > 0)ことによって特徴付けられます。同じ論理によって、逆の過程(凍結)では、エントロピーの減少(ΔS < 0)を示します。
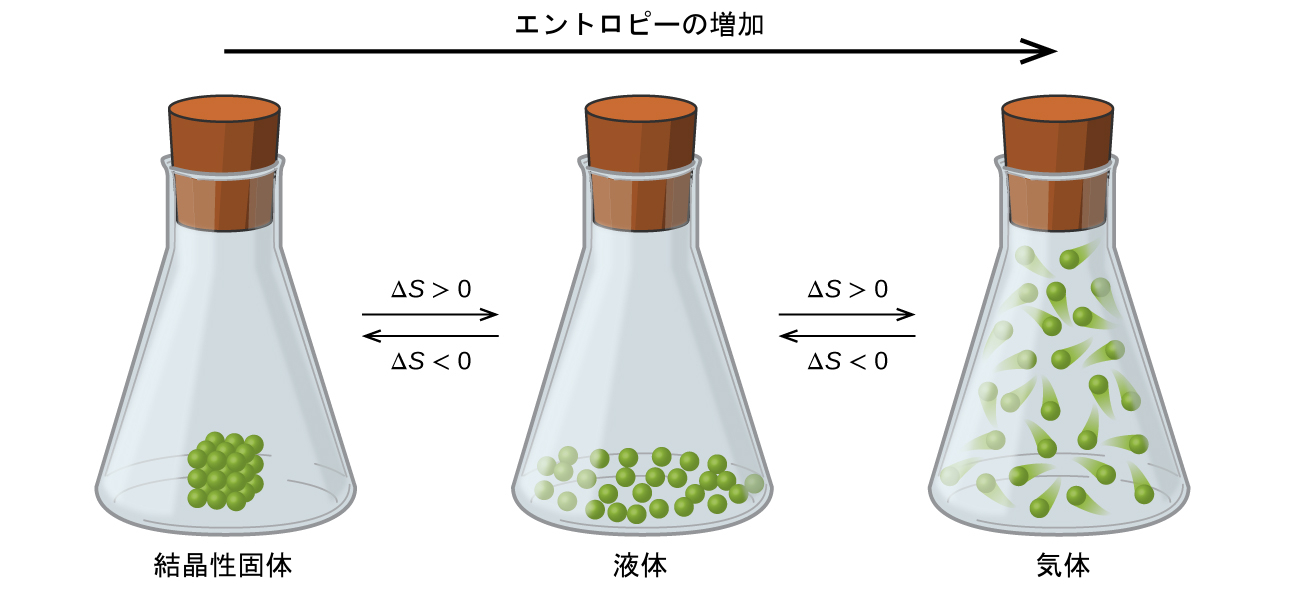
図16.10 | 物質のエントロピーは、比較的秩序のある固体からそれよりも秩序のない液体へ、そしてさらに秩序のない気体へと変化するにつれて増加します(ΔS > 0)。物質が気体から液体へ、そして固体へと変化するにつれて、エントロピーは減少します(ΔS < 0)。
ここで、気相を考えてみましょう。気相では、所与の数の原子や分子は、液相のときよりもはるかに大きな体積を占めます。それぞれの原子や分子は、より多くの位置(より多くの微視的状態に対応しています)に存在することができます。その結果、どのような物質でも、S気体 > S液体 > S固体となり、蒸発と昇華の過程では、同様にエントロピーが増加(ΔS > 0)します。 同様に、逆の相転移である凝縮と凝結の過程では、エントロピーが減少(ΔS < 0)します。
分子運動論によると、物質の温度はその粒子の平均運動エネルギーに比例します。物質の温度を上げると、固体では粒子の振動が大きくなり、液体や気体では粒子の移動が速くなります。高い温度では、物質の原子や分子間の運動エネルギーの分布も、低い温度のときに比べてより広くなります(より分散します)。したがって、任意の物質のエントロピーは温度とともに増加します(図16.11)。
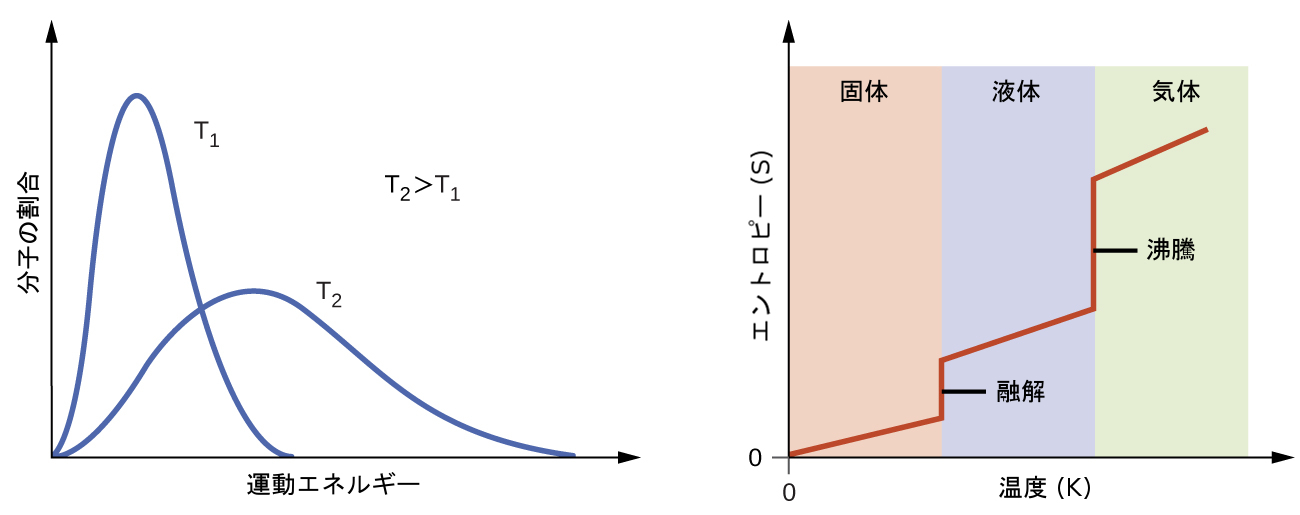
図16.11 | 物質の温度が上がるにつれてエントロピーは増加し、これは運動エネルギーの広がりが大きくなることに対応しています。物質が相転移を起こすと、エントロピーは著しく変化します。
学習へのリンク
物理的状態と温度に対する粒子の位置と運動の自由度の依存性をインタラクティブに可視化したこのシミュレータ(http://openstaxcollege.org/l/16freemotion)を試してみてください。
物質のエントロピーは、物質を構成する粒子(原子または分子)の構造によって影響されます。原子からなる物質については、所与の温度では、重い原子の方が軽い原子よりも大きなエントロピーを有しています。これは、粒子の質量と量子化された並進エネルギー準位の間隔との関係の結果です(この教科書の範囲を超えた話題)。分子の場合、原子の数が多いほど、分子が振動することのできる方法の数が増え、可能な微視的状態の数と系のエントロピーが増加します。
最後に、粒子の種類の違いが系のエントロピーに影響します。すべての粒子が同じである純物質と比較すると、2つかそれ以上の異なる種類の粒子の混合物のエントロピーは大きくなります。これは、非同一成分からなる系では、追加の配置や相互作用が可能であるためです。たとえば、固体が液体に溶解するとき、固体の粒子は、より大きな運動の自由度、および、溶媒粒子との追加の相互作用の両方を経験します。これは、物質とエネルギーのより均一な分散、そして、より多くの微視的状態に対応します。したがって、溶解の過程では、エントロピーが増加(ΔS > 0)します。
エントロピーに影響を与えるさまざまな要因を考慮することで、例題16.3に示されているように、さまざまな化学的・物理的プロセスにおけるΔSの符号について、情報に基づいた予測を行うことができます。
例題16.3 ΔSの符号の予測
以下のプロセスのエントロピー変化の符号を予測してください。それぞれの予測の理由を示してください。
(a)室温での1モルの液体の水 ⟶ 50 °Cでの1モルの液体の水
(b)Ag⁺(aq) + Cl⁻(aq) ⟶ AgCl(s)
(c)\(\rm C_6H_6(l) + \frac{15}{2} O₂(g) ⟶ 6CO_2(g) + 3H_2O(l)\)
(d)NH₃(s) ⟶ NH₃(l)
解法
(a)正、温度が上昇しています
(b)負、溶液中のイオン(粒子)の数が減少しているため、物質の分散が減少しています
(c)負、気体の種の量が正味で減少しています
(d)正、固体から液体への相転移のため、物質の分散が正味で増加しています
学習内容の確認
以下のプロセスのエントロピー変化の符号を予測してください。それぞれの予測の理由を示してください。
(a)NaNO₃(s) ⟶ Na⁺(aq) + NO₃⁻(aq)
(b)液体の水の凍結
(c)CO₂(s) ⟶ CO₂(g)
(d)CaCO(s) ⟶ CaO(s) + CO₂(g)
解答:(a)正:固体が溶解して溶液中で移動できるイオンが増加しています。(b)負:液体はより秩序のある固体になっています。(c)正:比較的秩序のあった固体が気体になっています。(d)正:気体の種の量が正味で増加しています。
16.3 熱力学の第二法則と第三法則
この節が終わるまでに、あなたは次のことができるようになります:
•熱力学の第二法則と第三法則を述べて、説明する
•標準条件下で相転移と化学反応のエントロピー変化を計算する
熱力学の第二法則
プロセスの自発性を信頼性をもって予測できる性質を特定するための探求では、ある有望な候補が特定されています:エントロピーです。系のエントロピーの増加(ΔS > 0)を伴うプロセスは、非常に多くの場合、自発的なものです。しかしながら、逆の例もたくさんあります。周囲を含めるようにエントロピーの変化についての考慮を拡張することによって、私たちはこの性質と自発性の間の関係に関する重要な結論が得られるかもしれません。熱力学的モデルでは、系とその周囲によってすべてのもの、すなわち宇宙が構成されているので、以下のことが成り立ちます:
\[ ΔS_{宇宙} = ΔS_{系} + ΔS_{周囲}\\ \]
この関係を説明するために、2つの物体(1つは系として、もう1つは周囲として特定されます)の間の熱流のプロセスをもう一度考えてみましょう。このようなプロセスには3つの可能性があります:
これらの物体が異なる温度にあり、温度の高い方の物体から温度の低い方の物体へと熱が流れます。これは自発的に起こることが常に観察されています。温度の高い方の物体を系として指定し、エントロピーの定義を用いると、以下のようになります:
\[ ΔS_{系} =\frac{−q_{可逆}}{T_{系}}\ および\ ΔS_{周囲} =\frac{q_{可逆}}{T_{周囲}}\\ \] −q可逆とq可逆の大きさは等しく、それらの反対の算術符号は系による熱の損失と周囲による熱の獲得を表しています。このシナリオでは、T系 > T周囲なので、系のエントロピーの減少は周囲のエントロピーの増加よりも小さくなり、宇宙のエントロピーは増加することになります:
\[ | ΔS_{系}| < | ΔS_{周囲}|\\ ΔS_{宇宙} = ΔS_{系} + ΔS_{周囲} > 0\\ \]これらの物体が異なる温度にあり、温度の低い方の物体から温度の高い方の物体へと熱が流れます。これは自発的に起こることは観察されていません。温度の高い方の物体を系として指定し、エントロピーの定義を用いると、以下のようになります:
\[ ΔS_{系} =\frac{q_{可逆}}{T_{系}}\ および\ ΔS_{周囲} =\frac{−q_{可逆}}{T_{周囲}}\\ \] q可逆の算術符号は、系による熱の獲得と周囲による熱の損失を表しています。周囲のエントロピー変化の大きさは、やはり系のエントロピー変化よりも大きくなりますが、この場合では、熱の変化の符号(つまり熱流の方向)によってΔS宇宙が負の値となります。このプロセスでは、宇宙のエントロピーが減少することになります。これらの物体が実質的に同じ温度T系 ≈ T周囲にあり、エントロピーの変化の大きさは系と周囲の両方で実質的に同じです。この場合、宇宙のエントロピー変化はゼロであり、系は平衡にあります。
\[ | ΔS_{系}| ≈ | ΔS_{周囲}|\\ ΔS_{宇宙} = ΔS_{系} + ΔS_{周囲} = 0\\ \]
これらの結果は、熱力学の第二法則として知られているエントロピーと自発性の関係についての深遠な記述へとつながります:すべての自発的な変化は宇宙のエントロピーの増加を引き起こします。これら3つの関係の要約が表16.1に与えられています。
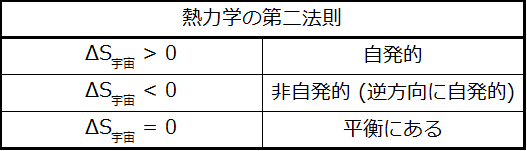
表16.1
多くの現実への適用では、周囲は系に比べて広大です。このような場合、何らかのプロセスの結果として周囲が得たり失ったりする熱は、その総熱エネルギーのごくわずかな、ほぼ無限小の量を表すことになります。たとえば、空気中での燃料の燃焼では、系(反応を起こす燃料と酸素分子)から、無限に質量の大きい周囲(地球の大気)への熱の移動を伴います。その結果、q周囲は q可逆の良い近似となり、第二法則は以下のように述べることができます:
\[ ΔS_{宇宙} = ΔS_{系} + ΔS_{周囲} = ΔS_{系} +\frac{q_{周囲}}{T}\\ \]
この式を使って、例題16.4に示されているようなプロセスの自発性を予測することができます。
例題16.4 氷は自発的に溶けるでしょうか?
プロセス:H₂O(s) ⟶ H₂O(l)のエントロピー変化は22.1J/Kであり、周囲が6.00kJの熱を系に伝達する必要があります。このプロセスは-10.00 °Cで自発的ですか?、+10.00 °Cで自発的ですか?
解法
宇宙のエントロピー変化を計算することによって、私たちはプロセスの自発性を見積もることができます。もしΔS宇宙が正であれば、プロセスは自発的です。両方の温度において、ΔS系 = 22.1 J/K、q周囲 = -6.00 kJです。−10.00 °C(263.15K)では、以下のようになります:
\[ \begin{eqnarray} ΔS_{宇宙} &=& ΔS_{系} + ΔS_{周囲}\\ &=& ΔS_{系} +\frac{q_{周囲}}{T}\\ &=& {\rm 22.1\ J/K +\frac{−6.00× 10^3\ J}{263.15\ K}}\\ &=& {\rm −0.7\ J/K}\\ \end{eqnarray} \]
ΔS宇宙 < 0なので、-10.0°Cでは融解は非自発的(自発的ではない)です。
10.00°C(283.15K)では、以下のようになります:
\[ \begin{eqnarray} ΔS_{宇宙} &=& ΔS_{系} +\frac{q_{周囲}}{T}\\ &=& {\rm 22.1\ J/K +\frac{−6.00× 10^3\ J}{283.15\ K}}\\ &=& {\rm +0.9\ J/K}\\ \end{eqnarray} \]
ΔS宇宙 > 0なので、10.00°Cでは融解は自発的です。
学習内容の確認
この情報を用いて、液体の水が同じ温度で自発的に凍結するかどうかを決定してください。ΔS宇宙の値についてあなたは何が言えますか?
解答:エントロピーは状態関数なので、ΔS凍結 = -ΔS融解 = -22.1J/K、q周囲 = +6.00kJとなります。−10.00 °Cでは自発的であり、+0.7 J/K、+10.00°Cでは非自発的であり、-0.9 J/Kとなります。
熱力学の第三法則
前の項では、系のエントロピーに寄与する物質とエネルギーの分散のさまざまな寄与について記述しました。これらの寄与を念頭に置いて、運動エネルギーを持たず(つまり、絶対零度の温度、0 K)、純粋で完全な結晶性固体のエントロピーを考えてみましょう。この系は、その純粋さ、完全な結晶性、運動の完全な欠如のために、結晶を構成するそれぞれの同一原子または分子にとっての可能な場所が1つしかないため、単一の微視的状態によって記述することができます(W = 1)。ボルツマン方程式によれば、この系のエントロピーはゼロです。
\[ S = k \ln W = k \ln(1) = 0\\ \]
系のエントロピーを制限するこの条件は、熱力学の第三法則を表しています:0 Kでの純粋で完全な結晶性物質のエントロピーはゼロです。
注意深い熱量測定を行うことによって、物質のエントロピーの温度依存性を決定し、特定の条件下での絶対エントロピーの値を導出することができます。標準エントロピー(S°)は、標準条件(圧力 1 bar、温度 298.15 K。標準条件の詳細については、この教科書の熱化学の章を参照)の下での1モルの物質についてのものです。反応の標準エントロピー変化(ΔS°)は、以下に示されるように、標準エントロピーを用いて計算することができます:
\[ ΔS° = ∑ νS°(生成物) − ∑ νS°(反応物)\\ \]
ここで、νは、プロセスを表すバランスの取れた反応式における化学量論的係数を表します。たとえば、室温での以下の反応
\[ m{\rm A} + n{\rm B} ⟶ x{\rm C} + y{\rm D}\\ \]
のΔS°はこのように計算されます:
\[ ΔS°=[xS ° ({\rm C}) + yS°({\rm D})] −[mS°({\rm A}) + nS°({\rm B})]\\ \]
標準エントロピーの一部が表16.2で与えられており、追加の値は付録Gで与えられています。以下の例題は、物理的および化学的プロセスの標準エントロピー変化を計算する際に、S°の値を使用することを例示しています。
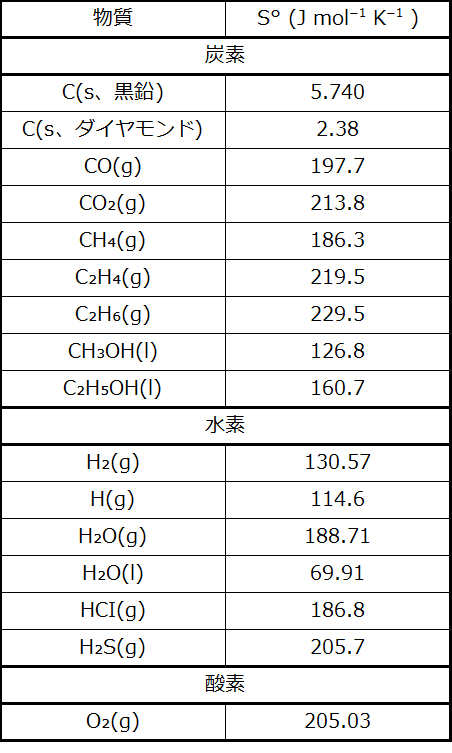
表16.2 | 1atmと298.15Kで測定された、選ばれた物質の標準エントロピー。(値は、現在認められている標準状態の圧力である1barで測定されたものとほぼ同じです。)
例題16.5 ΔS°の決定
以下のプロセスの標準エントロピー変化を計算してください:
\[ {\rm H_2 O\ (g) ⟶ H_2 O\ (l)}\\ \]
解法
上記のように標準エントロピーを用いてエントロピー変化を計算します:
\[ ΔS ° = {\rm (1\ mol)(70.0\ J\ mol^{−1}\ K^{−1}) − (1\ mol)(188.8\ J\ mol^{−1}\ K^{−1}) = −118.8\ J/K}\\ \]
ΔS°の値は、前の節で議論したように、この相転移(凝縮)では予想通り負の値となります。
学習内容の確認
以下のプロセスの標準エントロピー変化を計算してください:
\[ {\rm H_2\ (g) + C_2 H_4\ (g) ⟶ C_2 H_6\ (g)}\\ \]
解答:−120.6 J K⁻¹ mol⁻¹
例題16.6 ΔS°の決定
メタノールCH₃OHの燃焼についての標準エントロピー変化を計算してください:
\[ {\rm 2CH_3 OH\ (l) + 3O_2\ (g) ⟶ 2CO_2\ (g) + 4H_2 O\ (l)}\\ \]
解法
上記のように標準エントロピーを用いてエントロピー変化を計算します。
\[ \begin{array}{ll} ΔS° = ∑ νS°(生成物) − ∑ νS°(反応物)\\ = [2\ {\rm mol}× S°\left({\rm CO_2\ (g)}\right) + 4\ {\rm mol}× S°\left({\rm H_2 O\ (l)}\right)] \\ \hspace{10pt} − [2\ {\rm mol}× S°\left({\rm CH_3 OH\ (l)}\right) + 3\ {\rm mol}× S°\left({\rm O_2\ (g)}\right)]\\ = [2(213.8) + 4 × 70.0] − [2(126.8) + 3(205.03)]\\ = −161.1\ {\rm J/K}\\ \end{array} \]
学習内容の確認
以下の反応についての標準エントロピー変化を計算してください:
\[ {\rm Ca(OH)_2\ (s) ⟶ CaO\ (s) + H_2 O\ (l)}\\ \]
解答:24.7 J K⁻¹ mol⁻¹
16.4 自由エネルギー
この節が終わるまでに、あなたは次のことができるようになります:
•ギブズの自由エネルギーを定義し、自発性との関係を記述する
•反応物と生成物の生成自由エネルギーを使用して、プロセスの自由エネルギー変化を計算する
•生成エンタルピーおよび反応物と生成物のエントロピーを使用して、プロセスの自由エネルギー変化を計算する
•温度がいくつかのプロセスの自発性にどのように影響するかを説明する
•標準自由エネルギー変化を平衡定数に関連付ける
熱力学の第二法則を使ってプロセスが自発的であるかどうかを決定する際の課題の1つは、系のエントロピー変化と周囲のエントロピー変化を測定する必要があるということです。系の性質のみの観点から定義された新しい熱力学的性質を伴う代替的なアプローチが、アメリカの数学者ジョサイア・ウィラード・ギブズによって19世紀後半に導入されました。この新しい性質はギブズの自由エネルギー(G)(または単に自由エネルギー)と呼ばれ、系のエンタルピーとエントロピーの観点から以下のように定義されます:
\[ G = H − TS\\ \]
自由エネルギーは状態関数であり、温度と圧力が一定の場合、自由エネルギー変化(ΔG)は以下のように表すことができます:
\[ ΔG = ΔH − TΔS\\ \]
(簡単のために、以下では添え字「系」は省略します。)
この系の性質とプロセスの自発性との間の関係性は、以前に導出した第二法則の式を思い出すことによって理解することができます:
\[ ΔS_{宇宙} = ΔS +\frac{q_{周囲}}{T}\\ \]
第一法則は、q周囲 = -q系 であることを必要とし、一定圧力ではq系 = ΔH となるので、この式は以下のように書き換えることができます:
\[ ΔS_{宇宙} = ΔS −\frac{ΔH}{T}\\ \]
この式の両辺に-Tを掛け、並べ替えると以下のようになります:
\[ −TΔS_{宇宙} = ΔH −TΔS\\ \]
この式を自由エネルギー変化について先ほどの式と比較すると、以下のような関係が示されます:
\[ ΔG = −TΔS_{宇宙}\\ \]
したがって、自由エネルギー変化は、以前に特定された自発性の指標ΔS宇宙と直接関連しており、プロセスの自発性についての信頼できる指標です。表16.3はプロセスの自発性とこれらの指標の算術符号との関係をまとめたものです。
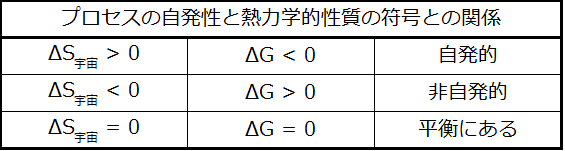
表16.3
ΔGの「自由」とは何のことか?
自由エネルギー変化は、自発性を示すことに加えて、自発過程によって達成されることのある有用な仕事の量(w)に関する情報も提供してくれます。この主題を厳密に扱うことは化学の入門教科書の範疇を超えていますが、簡単な議論はこの重要な熱力学的性質をよりよく理解するのに役立ちます。
この目的のために、エントロピーの減少を伴う自発的な発熱過程を考えてみましょう。以下のように定義される自由エネルギー
\[ ΔG = ΔH − TΔS \]
は、プロセスによって生成されるエネルギーΔHと、周囲に失われるエネルギーTΔSの差を表しているものと解釈することができます。生成されたエネルギーと失われたエネルギーの差は、そのプロセスによって有用な仕事をするために利用可能な(すなわち「自由な」)エネルギーΔGです。何らかのやり方で熱力学的可逆性の条件下でプロセスを発生させることができれば、行われる仕事の量は最大になるでしょう:
\[ ΔG = w_{\rm max}\\ \]
しかしながら、本章で以前に述べたように、そのような条件は現実的ではありません。さらに、自発過程から仕事を抽出するために使用される技術(たとえば、自動車エンジン、蒸気タービン)は決して100%効率的ではないため、これらのプロセスによって行われる仕事は常に理論上の最大値よりも小さくなります。同様の推論を非自発過程にも適用することができますが、その場合、自由エネルギー変化は、プロセスを実行するために系に対してなされなければならない最小の仕事の量を表します。
自由エネルギー変化を計算する
自由エネルギーは状態関数なので、その値は系の初期状態と最終状態の条件にのみ依存します。物理的・化学的反応についての自由エネルギー変化を計算するための便利で一般的なアプローチは、広く利用可能な標準状態の熱力学データをまとめたものを使用することです。1つの方法は、以下の関係に従って標準自由エネルギー変化ΔG°を計算するために、標準エンタルピーと標準エントロピーを使用することです。
\[ ΔG° = ΔH° − TΔS°\\ \]
例題16.7 ΔG°を計算するために標準エンタルピー変化と標準エントロピー変化を使用する
付録Gの標準エンタルピーと標準エントロピーのデータを使用して、室温(298 K)での水の蒸発についての標準自由エネルギー変化を計算してください。計算されたΔG°の値は、このプロセスの自発性について何を示していますか?
解法
関心のあるプロセスは以下の通りです:
\[ {\rm H_2 O\ (l) ⟶ H_2 O\ (g)} \]
標準自由エネルギー変化は、以下の式を用いて計算することができます:
\[ ΔG° = ΔH° − TΔS°\\ \]
付録Gより

付録のデータを使用して、標準エンタルピー変化と標準エントロピー変化を計算すると、以下が得られます:
\[ \begin{eqnarray} ΔH° &=& ΔH_{\rm f} °\left({\rm H_2 O\ (g)}\right) − ΔH_{\rm f} °\left({\rm H_2 O\ (l)}\right)\\ &=&{\rm [−241.82\ kJ/mol − (−286.83)\ kJ/mol] = 45.01\ kJ}\\ ΔS° &=& 1\ {\rm mol}× S°\left({\rm H_2 O\ (g)}\right) − 1\ {\rm mol}× S°\left({\rm H_2 O\ (l)}\right)\\ &=& {\rm (1\ mol)188.8\ J/mol·K − (1\ mol)70.0\ J/mol·K = 118.8\ J/K}\\ \end{eqnarray} \]
標準自由エネルギーの方程式に代入すると、以下のようになります:
\[ \begin{eqnarray} ΔG° &=& ΔH° − TΔS°\\ &=& {\rm 45.01\ kJ − (298\ K × 118.8\ J/K) ×\frac{1\ kJ}{1000\ J}}\\ &=& {\rm 45.01\ kJ − 35.4\ kJ}\\ &=& {\rm 9.6\ kJ}\\ \end{eqnarray} \]
298 K (25 °C)でΔG° > 0なので、沸騰は非自発的です(自発的ではありません)。
学習内容の確認
付録Gの標準エンタルピーと標準エントロピーのデータを使用して、ここに示されている反応(298 K)についての標準自由エネルギー変化を計算してください。計算されたΔG°の値は、このプロセスの自発性について何を示していますか?
\[ {\rm C_2 H_6\ (g) ⟶ H_2\ (g) + C_2 H_4\ (g)}\\ \]
解答:ΔG° = 102.0 kJ/mol。反応は25°Cでは非自発的です(自発的ではありません)。
ある反応についての標準自由エネルギー変化は、反応に関与する反応物と生成物の標準生成自由エネルギーΔGf °の値から計算することもできます。標準生成自由エネルギーは、標準的な状態で、その元素から物質の1モルを生成するのに伴う自由エネルギー変化です。標準生成エンタルピーと同様に、ΔGf °は、その定義上、標準状態の条件下での元素物質についてゼロとなります。ΔGf °値から反応のΔG °を計算するために使用されるアプローチは、エンタルピーとエントロピーの変化について以前に示したものと同じです。この反応
\[ m{\rm A} + n{\rm B} ⟶ x{\rm C} + y{\rm D}\\ \]
の場合では、室温での標準自由エネルギー変化は、以下のように計算することができます。
\[ \begin{eqnarray} ΔG° &=& ∑ ν ΔG°(生成物) − ∑ ν ΔG°(反応物)\\ &=&[xΔG_{\rm f} ° ({\rm C}) + yΔG_{\rm f} ° ({\rm D})] −[mΔG_{\rm f} ° ({\rm A}) + nΔG_{\rm f} ° ({\rm B})]\\ \end{eqnarray} \]
例題16.8 ΔG°を計算するために標準生成自由エネルギーを使用する
黄色の酸化水銀(II)の分解を考えてみましょう。
\[ {\rm HgO\ (s、黄色) ⟶ Hg\ (l) +\frac{1}{2} O_2\ (g)}\\ \]
室温での標準自由エネルギー変化ΔG°を、(a)標準生成自由エネルギーを使って、(b)標準生成エンタルピーと標準生成エントロピーを使って、計算してください。その結果は、この反応が標準条件下で自発的であることを示していますか、それとも非自発的であることを示していますか?
解法
必要なデータは付録Gに記載されており、以下に示されています。
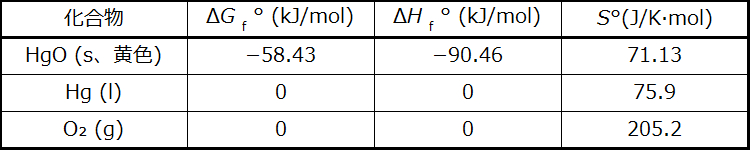
(a)生成自由エネルギーを使用すると:
\[ \begin{eqnarray} ΔG° &=& ∑ νG_{\rm f} ° (生成物) − ∑ νΔG_{\rm f} ° (反応物)\\ &=&\left[1ΔG{\rm _f° Hg\ (l)} +\frac{1}{2} ΔG{\rm _f° O_2\ (g)}\right]− 1ΔG{\rm _f ° HgO\ (s、黄色)}\\ &=&{\rm \left[1\ mol(0\ kJ/mol) +\frac{1}{2}\ mol(0\ kJ/mol)\right]− 1\ mol(−58.43\ kJ/mol)}\\ &=& {\rm 58.43\ kJ/mol}\\ \end{eqnarray} \]
(b)生成エンタルピーと生成エントロピーを使用すると:
\[ \begin{eqnarray} ΔH° &=& ∑ νΔH_{\rm f} ° (生成物) − ∑ νΔH_{\rm f} ° (反応物)\\ &=&\left[1ΔH{\rm _f ° Hg\ (l)} +\frac{1}{2} ΔH{\rm _f° O_2\ (g)}\right]− 1ΔH{\rm _f ° HgO\ (s、黄色)}\\ &=&{\rm \left[1\ mol(0\ kJ/mol) +\frac{1}{2}\ mol(0\ kJ/mol)\right]− 1\ mol(−90.46\ kJ/mol)}\\ &=& {\rm 90.46\ kJ/mol}\\ ΔS° &=& ∑ νΔS°(生成物) − ∑ νΔS°(反応物)\\ &=&\left[1ΔS°{\rm Hg\ (l)} +\frac{1}{2} ΔS°{\rm O_2\ (g)}\right]− 1ΔS°{\rm HgO\ (s、黄色)}\\ &=&{\rm \left[1\ mol(75.9\ J/mol·K) +\frac{1}{2}\ mol(205.2\ J/mol·K)\right]− 1\ mol(71.13\ J/mol·K)}\\ &=& {\rm 107.4\ J/mol·K}\\ ΔG° &=& ΔH° − TΔS° = {\rm 90.46\ kJ − 298.15\ K × 107.4\ J/K·mol ×\frac{1\ kJ}{1000\ J}}\\ ΔG° &=& {\rm (90.46 − 32.01)\ kJ/mol = 58.45\ kJ/mol}\\ \end{eqnarray} \]
25°Cでの標準自由エネルギー変化を計算する2つの方法は、どちらも同じ数値(3つの有効数字まで)を与え、どちらも室温ではこのプロセスが非自発的である(自発的ではない)ことを予測します。
学習内容の確認
ΔG°を、(a)生成自由エネルギーを使って、(b)生成エンタルピーと生成エントロピー(付録G)を使って、計算してください。その結果は、この反応が25 °Cで自発的であることを示していますか、それとも非自発的であることを示していますか?
\[ {\rm C_2 H_4\ (g) ⟶ H_2\ (g) + C_2 H_2\ (g)}\\ \]
解答:(a)140.8 kJ/mol、非自発的、(b)141.5 kJ/mol、非自発的
結合反応の自由エネルギー変化
ΔGが状態関数であるため、上記のような反応の自由エネルギー変化を計算する際に生成自由エネルギーを使用することが可能であり、そのアプローチはエンタルピーの変化を計算する際にヘスの法則を使用するのと類似しています(熱化学の章を参照してください)。例として水の蒸発を考えてみましょう:
\[ {\rm H_2 O\ (l) → H_2 O\ (g)}\\ \]
このプロセスを表す反応式は、水の2つの相についての生成反応を足し合わせることによって導出することができます(液相の反応は逆にする必要があります)。足し合わせた反応の自由エネルギー変化は、足し合わせる2つの反応の自由エネルギー変化の総和です:
\[ \begin{array}{ll} {\rm H_2\ (g) +\frac{1}{2} O_2\ (g) → H_2 O\ (g)} \hspace{20pt} ΔG_{\rm f} °気体\\ {\rm H_2 O\ (l) → H_2\ (g) +\frac{1}{2} O_2\ (g)} \hspace{20pt} − ΔG_{\rm f} °液体\\ \hline {\rm H_2 O\ (l) → H_2 O\ (g)} \hspace{65pt} ΔG ° = ΔG_{\rm f} °気体 − ΔG_{\rm f} °液体\\ \end{array} \]
このアプローチは、自発的反応と結合することによって非自発的反応が可能になる場合にも使用することができます。たとえば、硫化亜鉛から元素の亜鉛を生成することは、ΔG°の正の値によって示されるように、熱力学的に不都合です:
\[ {\rm ZnS\ (s) → Zn\ (s) + S\ (s)} \hspace{20pt} ΔG_1 ° = {\rm 201.3\ kJ}\\ \]
硫化鉱から亜鉛を生成するための工業的プロセスでは、上の分解反応を熱力学的に都合の良い硫黄の酸化反応に結合させます:
\[ {\rm S\ (s) + O_2\ (g) → SO_2\ (g)} \hspace{20pt} ΔG_2 ° = {\rm −300.1\ kJ}\\ \]
結合反応は負の自由エネルギー変化を示し、自発的です:
\[ {\rm ZnS\ (s) + O_2\ (g) → Zn\ (s) + SO_2\ (g)} \hspace{20pt} ΔG ° = {\rm 201.3\ kJ + (− 300.1\ kJ) = − 98.8\ kJ}\\ \]
このプロセスは一般的に高温で行われますので、標準自由エネルギーの値を用いて得られるこの結果は単なる推定値に過ぎません。しかしながら、計算の要点は同じです。
例題16.9 結合反応の自由エネルギー変化を計算する
標準条件下では、ZnSの分解とH₂Sの生成を結合した反応は自発的であると予想されるでしょうか?
解法
上記で概説されたアプローチに従って、付録Gの自由エネルギーの値を使用します:
\[ \begin{array}{ll} 硫化亜鉛の分解: {\rm ZnS\ (s) → Zn\ (s) + S\ (s)} \hspace{42pt} ΔG_1 ° = {\rm 201.3\ kJ}\\ 硫化水素の生成: {\rm S\ (s) + H_2\ (g) → H_2 S\ (g)} \hspace{40pt} ΔG_2 ° = {\rm − 33.4\ kJ}\\ 結合反応: {\rm ZnS\ (s) + H_2\ (g) → Zn\ (s) + H_2 S\ (g)} \hspace{20pt} ΔG° = {\rm 201.3\ kJ + (− 33.4\ kJ) = 167.9\ kJ}\\ \end{array} \]
結合反応は、正の自由エネルギー変化を示し、したがって、非自発的です。
学習内容の確認
以下の反応の標準自由エネルギー変化は何ですか?この反応は標準条件下で自発的であると予想されるでしょうか?
\[ {\rm FeS\ (s) + O_2\ (g) → Fe\ (s) + SO_2\ (g)}\\ \]
解答:−199.7 kJ、自発的です
自発性の温度依存性
以前にこの章のエントロピーの節で示したように、プロセスの自発性は系の温度に依存することがあります。たとえば、相転移は、問題としている物質の温度に応じて、一方の方向または他方の方向に自発的に進行します。同様に、いくつかの化学反応も温度に依存した自発性を示すことがあります。この概念を説明するために、自由エネルギー変化とプロセスのエンタルピー変化・エントロピー変化とを関連付ける式を検討します:
\[ ΔG = ΔH − TΔS\\ \]
プロセスの自発性(自由エネルギー変化の算術符号に反映されています)は、エンタルピー変化およびエントロピー変化の符号と、場合によっては絶対温度によって決定されます。Tは絶対温度(ケルビン)なので、正の値しか持てません。したがって、エンタルピー変化とエントロピー変化の符号に関して、4つの可能性があります:
ΔHとΔSの両方が正。この条件は、系のエントロピーの増加を伴う吸熱過程を記述しています。この場合、TΔS項の大きさがΔHよりも大きい場合、ΔGは負になります。TΔS項の大きさがΔHよりも小さい場合、自由エネルギー変化は正となります。このようなプロセスは、高温では自発的であり、低温では非自発的です。
ΔHとΔSの両方が負。この条件は、系のエントロピーの減少を伴う発熱過程を記述しています。この場合、TΔS項の大きさがΔHよりも小さい場合、ΔGは負になります。TΔS項の大きさがΔHよりも大きい場合、自由エネルギー変化は正となります。このようなプロセスは、低温では自発的であり、高温では非自発的です。
ΔHが正でΔSが負。この条件は、系のエントロピーの減少を伴う吸熱過程を記述しています。この場合、ΔGは温度に関係なく正となります。このようなプロセスは、すべての温度で非自発的です。
ΔHが負でΔSが正。この条件は、系のエントロピーの増加を伴う発熱過程を記述しています。この場合、ΔGは温度に関係なく負となります。このようなプロセスは、すべての温度で自発的です。
これら4つのシナリオが、図16.12にまとめられています。
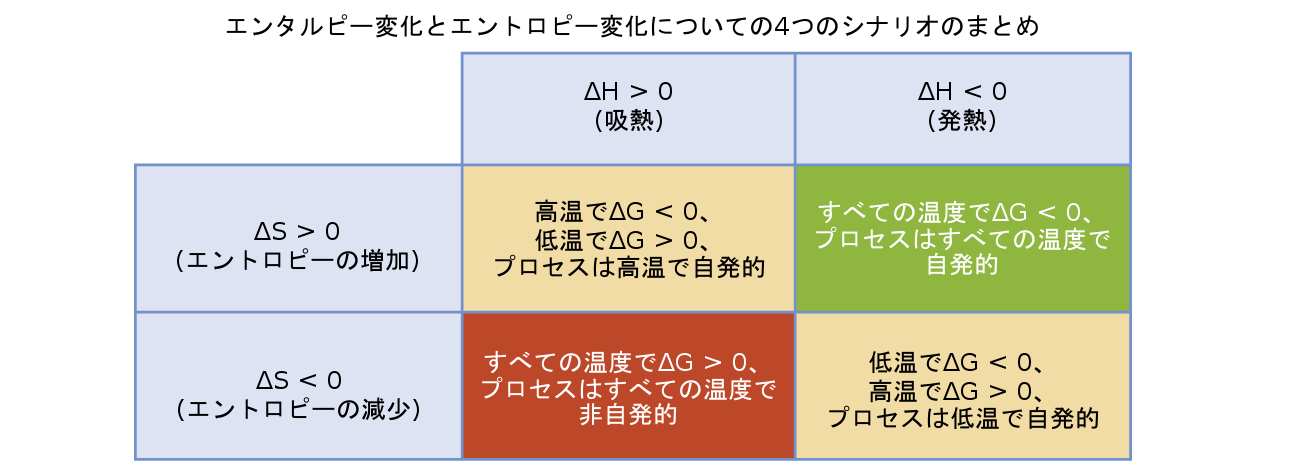
図16.12 | エンタルピー変化とエントロピー変化の符号に関して、4つの可能性があります。
例題16.10 自発性の温度依存性を予測する
炭素の不完全燃焼は以下の反応式で表されます:
\[ {\rm 2C\ (s) + O_2\ (g) ⟶ 2CO\ (g)}\\ \]
このプロセスの自発性は温度にどのように依存していますか?
解法
燃焼プロセスは発熱性(ΔH < 0)です。この特定の反応は、気体の種の量の増加に伴うエントロピーの増加を伴います(気体1モルの正味の増加、ΔS > 0)。したがって、この反応は、すべての温度で自発的(ΔG < 0)です。
学習内容の確認
人気のある化学的なハンドウォーマーは、鉄の空気酸化によって発熱します:
\[ {\rm 4Fe\ (s) + 3O_2\ (g) ⟶ 2Fe_2 O_3\ (s)}\\ \]
このプロセスの自発性は温度にどのように依存していますか?
解答:ΔHとΔSは負の値であり、反応は低温で自発的です。
自発性の温度依存性に関して導き出された結論を検討する際には、「高い」と「低い」という用語が何を意味するのかを念頭に置いておくことが重要です。これらの用語は形容詞であるため、問題としている温度は何らかの参照温度との相対的な高さまたは低さとみなされます。ある温度では非自発的であるが、別の温度では自発的であるプロセスは、温度が変化するにつれて、必然的に「自発性」を変化させることになります(そのΔGによって反映されます)。これは、ΔGをy軸に対して、Tをx軸に対してプロットした自由エネルギー変化の式のグラフ表示によって明確に示されます:
\[ ΔG = ΔH − TΔS\\ y = b + mx\\ \]
このようなプロットが図16.13に示されています。 エンタルピー変化とエントロピー変化が同じ算術符号であるプロセスは、プロットの2本の黄色の線によって描かれているように、温度に依存した自発性を示します。それぞれの線は、問題としているプロセスに特徴的な温度において、ある自発性の領域(正または負のΔG)から他の領域へと移行しています。この温度は、線のx-切片、すなわち、ΔGがゼロになるようなTの値によって表されます:
\[ ΔG = 0 = ΔH − TΔS\\ T =\frac{ΔH}{ΔS}\\ \]
したがって、あるプロセスが「高温」で自発的に起こるということは、そのプロセスのΔGがゼロになる温度を超えた温度であることを意味し、プロセスが「低温」で自発的に起こるということは、そのプロセスのΔGがゼロになる温度未満の温度であることを意味します。先に述べたように、ΔG = 0 の条件は系が平衡にあることを表しています。
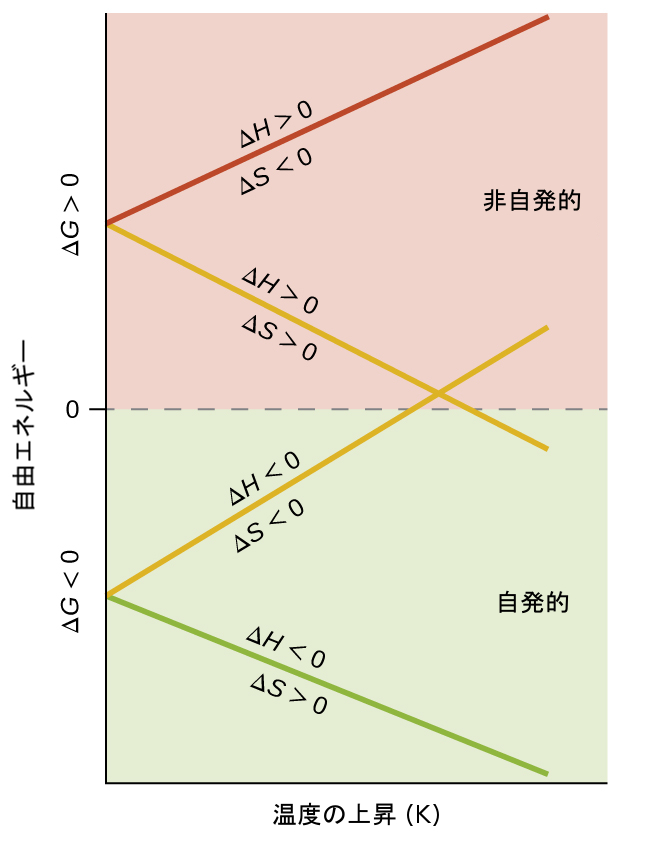
図16.13 | これらのプロットは、ΔHとΔSの4つの可能な算術符号の組み合わせについて、温度によるΔGの変化を示しています。
例題16.11 相転移の平衡温度
液体と固体の章で定義されているように、液体の沸点とは、液体と気体の相が平衡にある(つまり、蒸発と凝縮が等しい速度で起こるときの)温度のことです。付録Gの情報を用いて、水の沸点を推定してください。
解法
関心のあるプロセスは、以下のような相変化です:
\[ {\rm H_2 O\ (l) ⟶ H_2 O\ (g)}\\ \]
この過程が平衡にあるとき、ΔG = 0であるので、以下が成り立ちます:
\[ 0 = ΔH° − TΔS°\ すなわち\ T =\frac{ΔH°}{ΔS°}\\ \]
付録Gの標準熱力学データを使用すると、
\[ \begin{eqnarray} ΔH° &=& 1\ {\rm mol}× ΔH{\rm _f °\left(H_2 O\ (g)\right) − 1\ mol}× ΔH{\rm _f °\left(H_2 O\ (l)\right)}\\ &=& {\rm (1\ mol) − 241.82\ kJ/mol − (1\ mol)(−286.83\ kJ/mol) = 44.01\ kJ}\\ ΔS° &=& 1\ {\rm mol}× ΔS°\left({\rm H_2 O\ (g)}\right) − 1\ {\rm mol}× ΔS°\left({\rm H_2 O\ (l)}\right)\\ &=& {\rm (1\ mol)188.8\ J/K·mol − (1\ mol)70.0\ J/K·mol = 118.8\ J/K}\\ T &=&\frac{ΔH°}{ΔS°}={\rm \frac{44.01 × 10^3\ J}{118.8\ J/K}= 370.5\ K = 97.3\ °C}\\ \end{eqnarray} \]
水の通常の沸点について一般に認められている値は373.2K(100.0°C)であり、この計算は妥当な程度に一致しています。使用されたエンタルピー変化とエントロピー変化のデータの値は、298 Kでの標準データ(付録G)から得られたものであることに注意してください。必要であれば、実際の沸点(または少なくともそれに近い温度)において決定されたエンタルピー変化とエントロピー変化を使用することによって、より正確な結果を得ることができます。
学習内容の確認
付録Gの情報を用いて、CS₂の沸点を推定してください。
解答:313 K (一般に認められている値は319 K)
自由エネルギーと平衡
プロセスの自由エネルギー変化は、プロセスを駆動させる力の尺度として見ることができます。ΔGが負の値であれば、プロセスを順方向へ駆動する力を表し、正の値であれば、プロセスを逆方向へ駆動する力を表します。ΔGが0のとき、順方向へと駆動する力と逆方向へと駆動する力は等しく、プロセスは両方の方向へと同じ速度で発生します(系は平衡にあります)。
平衡の章では、平衡系の状態を表す便利な尺度として反応商Qが導入されました。Qは系の質量作用の式の数値であり、その値を使って平衡を達成するために反応がどの方向に進むかを特定することができるということを思い出してください。Qが平衡定数Kよりも小さい場合、反応は、平衡に達してQ = Kになるまで順方向へと進みます。逆にQ > Kの場合、反応は、平衡に達するまで逆方向に進みます。
非標準的な条件(1bar以外の圧力、1M以外の濃度)にある反応物と生成物でもって行われるプロセスの自由エネルギー変化は、以下の式に従って標準自由エネルギー変化に関連付けられます:
\[ ΔG = ΔG° + RT \ln Q\\ \]
Rは気体定数(8.314 J/K mol)、Tはケルビンすなわち絶対温度、Qは反応商です。気相平衡には、圧力をベースにした反応商Qpが用いられます。凝縮相平衡には濃度をベースにした反応商Qcが用いられます。この式は、例題16.12で示されるように、任意の一組の条件下でのプロセスの自発性を予測するために使用することができます。
例題16.12 非標準条件下でのΔGを計算する
ここに示されたプロセスについて、以下に指定された条件下での自由エネルギー変化は何ですか?
\[ T = {\rm 25 °C}、P_{\rm N_2} = {\rm 0.870\ atm}、P_{\rm H_2} = {\rm 0.250\ atm}、および P_{\rm NH_3} = {\rm 12.9\ atm}\\ {\rm 2NH_3\ (g) ⟶ 3H_2\ (g) + N_2\ (g)} \hspace{20pt} ΔG° = {\rm 33.0\ kJ/mol}\\ \]
解法
自由エネルギー変化と、標準自由エネルギー変化および反応商とを関係付ける式を直接使用することができます:
\[ \begin{eqnarray} ΔG &=& ΔG° + RT \ln Q\\ &=& \rm 33.0\ \frac{kJ}{mol}+\left(8.314\frac{J}{mol\ K}× 298\ K × \ln \frac{(0.250^3) × 0.870}{12.9^2}\right)\\ &=& \rm 9680\ \frac{J}{mol}\ すなわち\ 9.68\ kJ/mol\\ \end{eqnarray} \]
ΔGについて計算された値が正であるので、これらの条件下ではこの反応は非自発的です。
学習内容の確認
この同じ反応について、それぞれの気体を0.100 molずつを含む5.00 Lの混合物中で、875 °Cでの自由エネルギー変化を計算してください。これらの条件下でこの反応は自発的ですか?
解答:ΔG = –123.5 kJ/mo、はい
平衡にある系では、Q = K、ΔG = 0 となり、前の式は以下のように書くことができます。
\[ 0 = ΔG° + RT \ln K\ (平衡で)\\ ΔG° = −RT \ln K\ または\ K = e^{− \frac{ΔG°}{RT}}\\ \]
この式の形式は、これら2つの本質的な熱力学的性質の間に有用なつながりを提供してくれます。そして、これを使って標準自由エネルギー変化から平衡定数を導出することができ、また、その逆も可能です。標準自由エネルギー変化と平衡定数の間の関係が表16.4にまとめられています。

表16.4
例題16.13 標準自由エネルギー変化を用いて平衡定数を計算する
Ag⁺(aq)、Cl⁻(aq)、および AgCl(s) の標準生成自由エネルギーがそれぞれ 77.1 kJ/mol、-131.2 kJ/mol、および -109.8 kJ/mol であるとして、AgCl の溶解度積 Ksp を計算してください。
解法
関心のある反応は以下の通りです:
\[ {\rm AgCl\ (s) ⇌ Ag^+\ (aq) + Cl^−\ (aq)} \hspace{20pt} K_{\rm sp} = {\rm [Ag^+][Cl^−]}\\ \]
まず、この反応の標準自由エネルギー変化を、その反応物と生成物の標準生成自由エネルギーを用いて計算します:
\[ \begin{eqnarray} ΔG° &=&[ΔG{\rm _f °\left(Ag^+\ (aq)\right)} + ΔG{\rm _f °\left(Cl^−\ (aq)\right)}] −[ΔG{\rm _f °\left(AgCl(s)\right)}]\\ &=& {\rm [77.1\ kJ/mol − 131.2\ kJ/mol] − [−109.8\ kJ/mol] = 55.7\ kJ/mol}\\ \end{eqnarray} \]
次に、この反応の平衡定数を、標準自由エネルギー変化から導出します:
\[ \begin{eqnarray} K_{\rm sp} &=& e^{− \frac{ΔG°}{RT}}= \exp \left(−\frac{ΔG°}{RT}\right)\\ &=& \exp \left(−\frac{\rm 55.7 × 10^3\ J/mol}{\rm 8.314\ J/mol·K× 298.15\ K}\right)\\ &=& \exp(−22.470) = e^{−22.470} = 1.74 × 10^{−10}\\ \end{eqnarray} \]
この結果は、付録Jに記載されている値と妥当な程度に一致しています。
学習内容の確認
付録Gで与えられている熱力学データを使用して、25 °Cでの四酸化二窒素の解離の平衡定数を計算してください。
\[ {\rm 2NO_2\ (g) ⇌ N_2 O_4\ (g)}\\ \]
解答:K = 6.9
この2つの本質的な熱力学的概念の間の関係をさらに説明するために、反応は最終的に平衡を確立する方向へと自発的に進むという観察を考えてみましょう。自由エネルギー変化と反応の進度(たとえばQの値に反映されるような)をプロットすることによって示されるように、系の自由エネルギーが最小化されるときに平衡が確立されます(図16.14)。もし系が非平衡の量(Q≠K)の反応物と生成物とで構成されている場合、反応は平衡を確立するために必要な方向へと自発的に進行するでしょう。
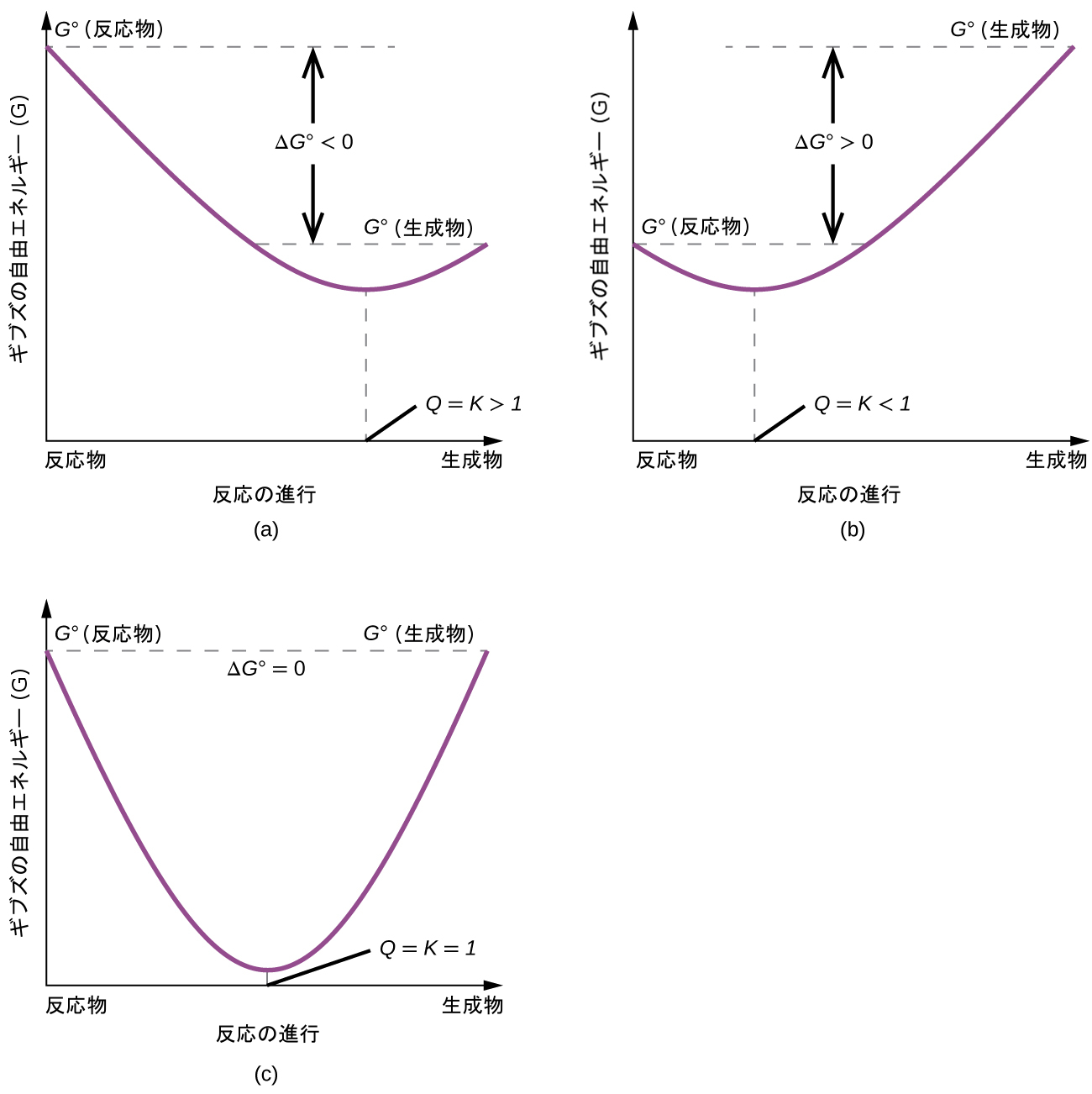
図16.14 | これらのプロットは、標準自由エネルギー変化が(a)負、(b)正、(c)ゼロである系の自由エネルギーと反応の進行を示しています。非平衡系では、自由エネルギーを最小化して平衡を確立するために必要な方向へと自発的に進行します。
重要用語
エントロピー(S):系内の物質および/またはエネルギーの分散の尺度である状態関数で、系の微視的状態の数によって決定される。しばしば系の無秩序さの尺度として記述される
ギブズの自由エネルギー変化(G):系のエンタルピーとエントロピーの観点から定義される熱力学的性質。すべての自発過程はGの減少を伴う
微視的状態:系内の物質とエネルギーの可能な構成または配置
非自発過程:外部の源からのエネルギーの継続的な投入を必要とするプロセス
可逆過程:条件のごく小さな変化に反応して方向を反転させることができるほどゆっくりと行われるプロセス。現実のプロセスによって近似することしかできない仮説的な構築物
熱力学の第二法則:すべての自発過程は宇宙のエントロピーの増加を伴う
自発過程:外部の源からのエネルギーの継続的な投入なしで行われるプロセス
標準エントロピー(S°):1barの圧力での物質1モルのエントロピー。表記される値は通常298.15 Kで決定される
標準エントロピー変化(ΔS°):標準エントロピーを用いて計算された、ある反応についてのエントロピーの変化
標準自由エネルギー変化(ΔG°):標準条件下(気体については1barの圧力、溶液については1Mの濃度)で発生するプロセスの自由エネルギーの変化
標準生成自由エネルギー(ΔGf°):標準的な状態で、その元素から物質の1モルを生成するのに伴う自由エネルギーの変化
熱力学の第三法則:絶対零度(0 K)での完全な結晶のエントロピーはゼロである
重要な方程式
\(•ΔS =\frac{q_{可逆}}{T}\)
\(•S = k \ln W\)
\(•ΔS = k \ln \frac{W_{\rm f}}{W_{\rm i}}\)
\(•ΔS° = ∑ νS°(生成物) − ∑ νS°(反応物)\)
\(•ΔS =\frac{q_{可逆}}{T}\)
\(•ΔS_{宇宙} = ΔS_{系} + ΔS_{周囲}\)
\(•ΔS_{宇宙} = ΔS_{系} + ΔS_{周囲} = ΔS_{系} +\frac{q_{周囲}}{T}\)
\(•ΔG = ΔH − TΔS\)
\(•ΔG = ΔG° + RT \ln Q\)
\(•ΔG° = −RT \ln K\)
この章のまとめ
16.1 自発性
化学的・物理的なプロセスは、ある特定の条件下で一方向に起こる自然な傾向を持っています。自発過程は、外部の源からのエネルギーの継続的な投入を必要とせずに生じるものであり、非自発過程はそのような投入を必要とします。自発過程を生じる系は、エネルギーを得ることも失うこともあるかもしれませんが、それらは物質および/またはエネルギーが系内で分配される方法の変化を経験することになります。
16.2 エントロピー
エントロピー(S)は、系の微視的状態の数(系を配置することのできる方法の数)と、ケルビン温度に対する可逆熱の比率とに関連する状態関数です。これは、系内の物質および/またはエネルギーの分散または分布の尺度として解釈されることがあり、しばしば系の「無秩序さ」を表すものとして記述されます。
ある所与の物質については、エントロピーは、S固体 < S液体 < S気体というように、その相に依存します。所定の温度で同じ物理的状態にある異なる物質の場合、エントロピーは通常、重い原子やより複雑な分子ほど大きくなります。エントロピーは、系が加熱されたり、溶液が形成されたりすると増加します。これらの指針を使用すると、いくつかの化学反応や物理的変化についてのエントロピー変化の符号を確実に予測することができます。
16.3 熱力学の第二法則と第三法則
熱力学の第二法則は、自発過程が宇宙のエントロピーを増加させる(S宇宙 > 0)ことを述べています。ΔS宇宙 < 0の場合、プロセスは非自発的であり、ΔS宇宙 = 0の場合、系は平衡にあります。熱力学の第三法則は、0 Kでの完全で純粋な結晶性固体では、エントロピーがゼロであることを認めています。微視的状態が1つしかない場合、エントロピーはゼロになります。私たちは、プロセスに関与する反応物と生成物の標準エントロピーの値を使用することによって、プロセスの標準エントロピー変化を計算することができます。
16.4 自由エネルギー
ギブズの自由エネルギー(G)は、系の量に関してのみ定義される状態関数であり、プロセスの自発性を予測するために使用することができます。ΔGの負の値は自発的なプロセスを示し、ΔGの正の値は非自発的なプロセスを示しています。そして、ΔGがゼロの場合は系が平衡にあることを示しています。自由エネルギー変化を計算するためには、いくつかのアプローチを使うことが可能です。
練習問題
16.1 自発性
1.自発的な反応とは何ですか?
2.非自発的な反応とは何ですか?
3.以下の過程が自発的であるか非自発的であるかを示してください。
(a)液体の水が凝固点未満の温度で凍結すること
(b)液体の水が凝固点超の温度で凍結すること
(c)ガソリンの燃焼
(d)空中に投げられたボール
(e)地面に落ちる雨粒
(f)湿潤な雰囲気で鉄が錆びること
4.ヘリウムを充填した風船は、ヘリウム原子が風船の壁を通過して拡散するために、一晩で自発的にしぼみます。この過程に伴う物質および/またはエネルギーの再分配について記述してください。
5.多くのプラスチック素材は、炭素と水素を含む有機ポリマーです。これらのプラスチックが空気中で酸化して二酸化炭素と水を生成する過程は自発過程です。しかしながら、プラスチック素材は環境中に残留する傾向があります。説明してください。
16.2 エントロピー
6.図16.8では、2つの箱の間で共有されている4つの異なる粒子についてのすべての可能な分布と微視的状態が示されています。もし粒子が最初は2つの箱の間に均等に分布していたものの、再分布したときにすべての粒子が箱(b)に収まった場合、そのエントロピー変化ΔSを決定してください。
7.図16.8では、2つの箱の間で共有されている4つの異なる粒子についてのすべての可能な分布と微視的状態が示されています。分布(b)から分布(d)に変換された場合、系のエントロピー変化ΔSを決定してください。
8.前の設問で記述したプロセスは、図16.4に示されている系とどのように関係していますか?
9.図16.8の系と似ているものの、4つではなく6つの粒子を含むような系を考えてみましょう。この場合、2つの箱のうち1つだけにすべての粒子が入っている確率は何ですか?これを、4つの粒子の系の同様の確率(私たちは1/8と導き出しました)と比較してみてください。この比較は、さらに大きな系について何を教えてくれるでしょうか?
10.図16.9に示されている系を考えてみましょう。エネルギーが最初は粒子Aだけに付随しているものの、最終状態ではエネルギーが2つの異なる粒子の間に分配されているようなプロセスについてのエントロピーの変化は何ですか?
11.図16.9に示されている系を考えてみましょう。エネルギーが最初は粒子AとBに付随しており、そしてエネルギーが異なる箱に入った2つの粒子の間に分配される(A-Bの箱に1つ、C-Dの箱にもう1つ)ようなプロセスについてのエントロピーの変化は何ですか?
12.以下の系の集合をエントロピーが大きくなる順に並べてください。それぞれの物質を1モルと仮定し、集合のそれぞれのメンバーは同じ温度であると仮定してください。
(a)H₂(g)、HBrO₄(g)、HBr(g)
(b)H₂O(l)、H₂O(g)、H₂O(s)
(c)He(g)、Cl₂(g)、P₄(g)
13.室温では、ハロゲンのエントロピーはI₂からBr₂、そしてCl₂へと増加していきます。説明してください。
14.I₂(s)の昇華とI₂(s)の融解という2つの過程を考えてみましょう(注:後者の過程は、同じ温度であるもののやや高い圧力で起こります)。
I₂(s) ⟶ I₂(g)
I₂(s) ⟶ I₂(l)
これらの過程では、ΔSは正でしょうか、負でしょうか? どちらの過程でエントロピー変化の大きさが大きくなるでしょうか?
15.与えられたペアの中で、どちらの物質のエントロピーの値が大きいかを示してください。あなたの選択を説明してください。
(a)C₂H₅OH(l)またはC₃H₇OH(l)
(b)C₂H₅OH(l)またC₂H₅OH(g)
(c)2H(g)またH(g)
16.以下の過程について、エントロピー変化の符号を予測してください。
(a)角氷が融点近くまで温められる。
(b)寒い朝に息を吐くと白くなる。
(c)雪が溶ける。
17.以下の過程について、エントロピー変化の符号を予測してください。あなたの予測の理由を述べてください。
(a)Pb²⁺(aq) + S²⁻(aq) ⟶ PbS(s)
(b)\(\rm 2Fe(s) + \frac{3}{2}O_2(g) ⟶ Fe_2O_3(s)\)
(c)2C₆H₁₄(l) + 19O₂(g) ⟶ 14H₂O(g) + 12CO₂(g)
18.メタンCH₄(g)を燃焼させて二酸化炭素と水蒸気が発生する際の、バランスの取れた化学反応式を書いてください。この化学反応について、ΔSが正か負かを予測することが難しい理由を説明してください。
19.ベンゼンC₆H₆(l)を燃焼させて二酸化炭素と水蒸気が発生する際の、バランスの取れた化学反応式を書いてください。この過程では、ΔSが正であると予測しますか、負であると予測しますか?
16.3 熱力学の第二法則と第三法則
20.ある化学的変化についてのΔSとΔS°との間の違いは何ですか?
21.以下の変化についてΔS°を求めてください。
(a)SnCl₄(l) ⟶ SnCl₄(g)
(b)CS₂(g) ⟶ CS₂(l)
(c)Cu(s) ⟶ Cu(g)
(d)H₂O(l) ⟶ H₂O(g)
(e)2H₂(g) + O₂(g) ⟶ 2H₂O(l)
(f)2HCl(g) + Pb(s) ⟶ PbCl₂(s) + H₂(g)
(g)Zn(s) + CuSO₄(s) ⟶ Cu(s) + ZnSO₄(s)
22.標準条件下で液体のエタノール(C₂H₅OH)を燃焼させて、気体の二酸化炭素と液体の水を得る際のエントロピー変化を決定してください。
23.標準条件下で気体のプロパン(C₃H₈)を燃焼させて、気体の二酸化炭素と水を得る際のエントロピー変化を決定してください。
24.「テルミット」反応は、鉄道のレールなどの金属部品の溶接や金属の精錬に利用されてきました。そのようなテルミット反応の1つは、Fe₂O₃(s) + 2Al(s) ⟶ Al₂O₃(s) + 2Fe(s)です。この反応は、標準条件下で室温では自発的でしょうか?反応の間に、周囲は851.8 kJ/molの熱を吸収します。
25.付録Gに記載されている関連するS°の値を用いて、以下の変化についてのΔS°を計算してください:
(a) N₂(g) + 3H₂(g) ⟶ 2NH₃(g)
(b) \(\rm N_2(g) + \frac{5}{2}O_2(g) ⟶ N_2O_5(g)\)
26.後続の情報から、以下のΔS°を求めてください:
N(g) + O(g) ⟶ NO(g) ΔS° = ?
N₂(g) + O₂(g) ⟶ 2NO(g) ΔS° = 24.8 J/K
N₂(g) ⟶ 2N(g) ΔS° = 115.0 J/K
O₂(g) ⟶ 2O(g) ΔS° = 117.0 J/K
27.それぞれの温度でΔS宇宙を計算することにより、1モルのNaCl(s)の融解が500°Cと700°Cで自発的に起こるかどうかを決定してください。
\[ S_{\rm NaCl(s)}^° = 72.11\ \frac{\rm J}{\rm mol·K}\\ S_{\rm NaCl(l)}^° = 95.06\ \frac{\rm J}{\rm mol·K}\\ ΔH_{溶融}^° = 27.95\ {\rm kJ/mol}\\ \]
この問題を解くために使用する熱力学的情報(エントロピーとエンタルピーの値)について、どのような仮定をしますか?
28.付録Gの標準エントロピーのデータを使用して、以下のそれぞれの反応についてのエントロピーの変化を決定してください。すべてのプロセスは標準条件下、25°Cで起こります。
(a)MnO₂(s) ⟶ Mn(s) + O₂(g)
(b)H₂(g) + Br₂(l) ⟶ 2HBr(g)
(c)Cu(s) + S(g) ⟶ CuS(s)
(d)2LiOH(s) + CO₂(g) ⟶ Li₂CO₃(s) + H₂O(g)
(e)CH₄(g) + O₂(g) ⟶ C(s, 黒鉛) + 2H₂O(g)
(f)CS₂(g) + 3Cl₂(g) ⟶ CCl₄(g) + S₂Cl₂(g)
29.付録Gの標準エントロピーのデータを使用して、以下のそれぞれの反応についてのエントロピーの変化を決定してください。すべてのプロセスは標準条件下、25°Cで起こります。
(a)C(s, 黒鉛) + O₂(g) ⟶ CO₂(g)
(b)O₂(g) + N₂(g) ⟶ 2NO(g)
(c)2Cu(s) + S(g) ⟶ Cu₂S(s)
(d)CaO(s) + H₂O(l) ⟶ Ca(OH)₂(s)
(e)Fe₂O₃(s) + 3CO(g) ⟶ 2Fe(s) + 3CO₂(g)
(f)CaSO₄⋅2H₂O(s) ⟶ CaSO₄(s) + 2H₂O(g)
16.4 自由エネルギー
30.ある化学的変化についてのΔGとΔG°との間の違いは何ですか?
31.ある反応は、ΔH° = 100 kJ/molおよびΔS° = 250 J/mol·Kです。この反応は室温で自発的ですか?そうでない場合、どのような温度条件下で自発的になりますか?
32.ある反応が、ΔG < 0(負)で始まり、ΔG = 0の点に達すると何が起こるかを説明してください。
33.付録Gの標準生成自由エネルギーのデータを使用して、標準状態の条件下、25 °Cで起こる以下のそれぞれの反応についての自由エネルギーの変化を決定してください。これらの条件で、それぞれが自発的であるか、または非自発的であるかを特定してください。
(a)MnO₂(s) ⟶ Mn(s) + O₂(g)
(b)H₂(g) + Br₂(l) ⟶ 2HBr(g)
(c)Cu(s) + S(g) ⟶ CuS(s)
(d)2LiOH(s) + CO₂(g) ⟶ Li₂CO₃(s) + H₂O(g)
(e)CH₄(g) + O₂(g) ⟶ C(s、黒鉛) + 2H₂O(g)
(f)CS₂(g) + 3Cl₂(g) ⟶ CCl₄(g) + S₂Cl₂(g)
34.付録Gの標準自由エネルギーのデータを使用して、標準状態の条件下、25 °Cで起こる以下のそれぞれの反応についての自由エネルギーの変化を決定してください。これらの条件で、それぞれが自発的であるか、または非自発的であるかを特定してください。
(a)C(s、黒鉛) + O₂(g) ⟶ CO₂(g)
(b)O₂(g) + N₂(g) ⟶ 2NO(g)
(c)2Cu(s) + S(g) ⟶ Cu₂S(s)
(d)CaO(s) + H₂O(l) ⟶ Ca(OH)₂(s)
(e)Fe₂O 3 (s) + 3CO(g) ⟶ 2Fe(s) + 3CO₂(g)
(f)CaSO₄·2H₂O(s) ⟶ CaSO₄(s) + 2H₂O(g)
35.以下が与えられたとします:
P₄(s) + 5O₂(g) ⟶ P₄O₁₀(s) ΔG° = −2697.0 kJ/mol
2H₂(g) + O₂(g) ⟶ 2H₂O(g) ΔG° = −457.18 kJ/mol
6H₂O(g) + P₄O₁₀(s) ⟶ 4H₃PO₄(l) ΔG° = −428.66 kJ/mol
(a)リン酸の標準生成自由エネルギーΔGf°を決定してください。
(b)あなたの計算結果は、付録Gの値と比較してどうですか?説明してください。
36.酸素O₂(g)からのオゾンO₃(g)の生成は、標準状態の条件下、室温で自発的ですか?
37.標準状態の条件下での赤色の酸化水銀(II)の分解を考えてみましょう。
2HgO(s、赤色) ⟶ 2Hg(l) + O₂(g)
(a)標準状態の条件下では、この分解は自発的でしょうか?
(b)この反応は何度よりも高い温度で自発的になるでしょうか?
38.理想的な宇宙船の制御スラスター用燃料は、とりわけ、適切な触媒にさらされたときに自発的な発熱反応で分解することができるべきです。適切な燃料の候補として、標準状態の条件下での以下の物質を評価してください。
(a)アンモニア:2NH₃(g) ⟶ N₂(g) + 3H₂(g)
(b)ジボラン:B₂H₆(g) ⟶ 2B(g) + 3H₂(g)
(c)ヒドラジン:N₂H₄(g) ⟶ N₂(g) + 2H₂(g)
(d)過酸化水素:H₂O₂(l) ⟶ H₂O(g) + (1/2)O₂(g)
39.与えられた温度での平衡定数から、以下のそれぞれの反応についてΔG°を計算してください。
(a)N₂(g) + O₂(g) ⟶ 2NO(g)
T = 2000 °C Kp = 4.1 × 10⁻⁴
(b)H₂(g) + I₂(g) ⟶ 2HI(g)
T = 400 °C Kp = 50.0
(c)CO₂(g) + H₂(g) ⟶ CO(g) + H₂O(g)
T = 980 °C Kp = 1.67
(d)CaCO₃(s) ⟶ CaO(s) + CO₂(g)
T = 900 °C Kp = 1.04
(e)HF(aq) + H₂O(l) ⟶ H₃O⁺(aq) + F⁻(aq)
T = 25 °C Kp = 7.2 × 10⁻⁴
(f)AgBr(s) ⟶ Ag⁺(aq) + Br⁻(aq)
T = 25 °C Kp = 3.3 × 10⁻¹³
40.与えられた温度での平衡定数から、以下のそれぞれの反応についてΔG°を計算してください。
(a)Cl₂(g) + Br₂(g) ⟶ 2BrCl(g)
T = 25 °C Kp = 4.7 × 10⁻²
(b)2SO₂(g) + O₂(g) ⇌ 2SO₃(g)
T = 500 °C Kp = 48.2
(c)H₂O(l) ⇌ H₂O(g)
T = 60 °C Kp = 0.196 atm
(d)CoO(s) + CO(g) ⇌ Co(s) + CO₂(g)
T = 550 °C Kp = 4.90 × 10²
(e)CH₃NH₂(aq) + H₂O(l) ⟶ CH₃NH₃⁺(aq) + OH⁻(aq)
T = 25 °C Kp = 4.4 × 10⁻⁴
(f)PbI₂(s) ⟶ Pb²⁺(aq) + 2I⁻(aq)
T = 25 °C Kp = 8.7 × 10⁻⁹
41.与えられたΔG°の値から、以下のそれぞれの反応について25°Cでの平衡定数を計算してください。
(a)O₂(g) + 2F₂(g) ⟶ 2OF₂(g)
ΔG° = −9.2 kJ
(b)I₂(s) + Br₂(l) ⟶ 2IBr(g)
ΔG° = 7.3 kJ
(c)2LiOH(s) + CO₂(g) ⟶ Li₂CO₃(s) + H₂O(g)
ΔG° = −79 kJ
(d)N₂O₃(g) ⟶ NO(g) + NO₂(g)
ΔG° = −1.6 kJ
(e)SnCl₄(l) ⟶ SnCl₄(l)
ΔG° = 8.0 kJ
42.与えられたΔG°の値から、以下のそれぞれの反応について25°Cでの平衡定数を計算してください。
(a)I₂(s) + Cl₂(g) ⟶ 2ICl(g)
ΔG° = −10.88 kJ
(b)H₂(g) + I₂(s) ⟶ 2HI(g)
ΔG° = 3.4 kJ
(c)CS₂(g) + 3Cl₂(g) ⟶ CCl₄(g) + S₂Cl₂(g)
ΔG° = −39 kJ
(d)2SO₂(g) + O₂(g) ⟶ 2SO₃(g)
ΔG° = −141.82 kJ
(e)CS₂(g) ⟶ CS₂(l)
ΔG° = −1.88 kJ
43.与えられた温度での平衡定数を計算してください。
(a)O₂(g) + 2F₂(g) ⟶ 2F₂O(g)
(T = 100 °C)
(b)I₂(s) + Br₂(l) ⟶ 2IBr(g)
(T = 0.0 °C)
(c)2LiOH(s) + CO₂(g) ⟶ Li₂CO₃(s) + H₂O(g)
(T = 575 °C)
(d)N₂O₃(g) ⟶ NO(g) + NO₂(g)
(T = −10.0°C)
(e)SnCl₄(l) ⟶ SnCl₄(g)
(T = 200 °C)
44.与えられた温度での平衡定数を計算してください。
(a)I₂(s) + Cl₂(g) ⟶ 2ICl(g)
(T = 100 °C)
(b)H₂(g) + I₂(s) ⟶ 2HI(g)
(T = 0.0 °C)
(c)CS₂(g) + 3Cl₂(g) ⟶ CCl₄(g) + S₂Cl₂(g)
(T = 125 °C)
(d)2SO₂(g) + O₂(g) ⟶ 2SO₃(g)
(T = 675 °C)
(e)CS₂(g) ⟶ CS₂(l)
(T = 90 °C)
45.298 Kでの以下の反応を考えてみましょう:
N₂O₄(g) ⇌ 2NO₂(g) Kp = 0.142
この温度での標準自由エネルギー変化は何ですか?初期の系(反応物と生成物は標準状態にあります)が平衡に近づくにつれて何が起きるかを記述してください。
46.ジクロロメタン(CH₂Cl₂)の通常の沸点(ケルビンで)を決定してください。インターネットや他の何らかの情報源を使って実際の沸点を調べ、温度の百分率誤差を計算してください。2つの値の間の違い(もしあるとして)を説明してください。
47.どのような条件下でN₂O₃(g) ⟶ NO(g) + NO₂(g)が自発的でしょうか?
48.室温において、水の自己イオン化の平衡定数(Kw)は 1.00 × 10⁻¹⁴です。この情報を用いて、水素イオンと水酸化物イオンが水を生成する水性反応の標準自由エネルギー変化を計算してください。(ヒント:この反応は自己イオン化反応の逆の反応です。)
49.硫化水素は天然ガスに含まれる汚染物質です。硫化水素を除去した後、それは以下の反応によって硫黄に変換されます。
\(\rm 2H_2S(g) + SO_2(g) ⇌ \frac{3}{8}S_8(s、斜方) + 2H_2O(l)\)
この反応の平衡定数は何ですか?この反応は吸熱性ですか、それとも発熱性ですか?
50.CaCO₃(s)がCaO(s)とCO₂(g)へと分解することを考えてみましょう。室温でのCO₂の平衡分圧は何ですか?
51.実験室では、塩化水素HCl(g)とアンモニアNH₃(g)の溶液の瓶からそれらが漏れ出して反応し、塩化アンモニウムNH₄Cl(s)を形成することがしばしばあります(塩化アンモニウムは、ガラス製品によく見られる白い薄膜です)。室内に漏れ出したそれぞれの気体のモル数が同じであると仮定すると、室温での実験室内のHClとNH₃の最大分圧は何ですか? (ヒント:分圧は等しくなり、平衡にあるときに最大値になります。)
52.ベンゼンはアセチレンから調製されます。
3C₂H₂(g) ⇌ C₆H₆(g)
25°Cと850°Cでの平衡定数を決定してください。これらの温度のいずれかで反応は自発的に起こりますか?アセチレンがすべてベンゼンとならないのはなぜですか?
53.二酸化炭素は高温でCOとO₂に分解します。1000°CでCO₂の初期圧力が1.15atmの試料において、酸素の平衡分圧は何ですか?
54.四塩化炭素は、重要な工業用溶媒であり、850Kでのメタンの塩素化によって調製されます。
CH₄(g) + 4Cl₂(g) ⟶ CCl₄(g) + 4HCl(g)
850 K でのこの反応の平衡定数は何ですか?反応の温度を一定に保つためには、反応容器を加熱する必要がありますか、それとも冷却する必要がありますか?
55.酢酸(CH₃CO₂H)は、気相中で二量体(CH₃CO₂H)₂を形成することができます。
2CH₃CO₂H(g) ⟶ (CH₃CO₂H)₂(g)
二量体は、二量体1モルあたり66.5kJの合計の強さを持つ2つの水素結合によって保持されています。
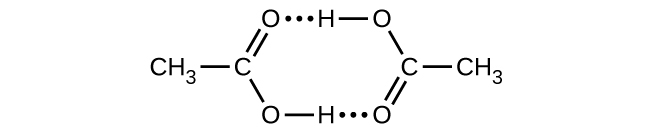
25°Cでの二量化の平衡定数は1.3×10³(atmでの圧力)です。この反応のΔS°は何ですか?
56.以下の反応のΔGºを決定してください。
(a)五塩化アンチモンは 448°Cで分解します。その反応は:
SbCl₅(g) ⟶ SbCl₃(g) + Cl₂(g)
448°Cでの5.00 L フラスコ内の平衡混合物には、3.85 g の SbCl₅、9.14 g の SbCl₃、2.84 g の Cl₂が含まれています。
(b)塩素分子はこの反応にしたがって解離します:
Cl₂(g) ⟶ 2Cl(g)
975 K、圧力1.00 atmで、1.00%のCl₂分子が解離します。
57.Pb²⁺(aq)およびCl⁻(aq)のΔGf°がそれぞれ-24.3 kJ/molおよび-131.2 kJ/molであることを考慮して、PbCl₂(s)の溶解度積Kspを決定してください。
58.Ag⁺(aq)およびAg₂S(s)のΔGf°がそれぞれ77.1 kJ/molおよび-39.5 kJ/molであり、Ag₂S(s)の溶解度積が8×10⁻⁵¹であることを考慮して、S²⁻(aq)の生成についての標準自由エネルギー変化ΔGf°を決定してください。
59.ダイヤモンドから黒鉛への変換についての標準エンタルピー変化、エントロピー変化、自由エネルギー変化を決定してください。エンタルピー変化とエントロピー変化について、変換の自発性について議論してください。ダイヤモンドが自発的に黒鉛に変化することが観察されない理由を説明してください。
60.水1モルの298Kでの蒸発は、8.58kJの標準自由エネルギー変化を有しています。
H₂O(l) ⇌ H₂O(g) ΔG° = 8.58 kJ
(a)標準的な熱力学的条件下では、水の蒸発は自発的に起こりますか?
(b)この物理過程についての平衡定数 Kpを決定してください。
(c)ΔGを計算することにより、水の分圧 PH₂Oが 0.011 atm のとき、298 K での水の蒸発が自発的であるかどうかを決定してください。
(d)室温で水の蒸発が常に非自発的である場合、濡れた洗濯物を外に干しても決して乾くことはないでしょう。洗濯物が乾くためには、空気中のPH₂Oの値は何でなければなりませんか?
61.解糖において、グルコース(Glu)がグルコース-6-リン酸(G6P)を生成する反応は、以下の式で表されるように、ATPが存在することを必要とします:
Glu + ATP ⟶ G6P + ADP ΔG° = −17 kJ
この過程で、ATPは以下の式で要約されるように、ADPになります:
ATP ⟶ ADP ΔG°= −30 kJ
以下の反応の標準自由エネルギー変化を決定し、このプロセスを駆動するためにATPが必要である理由を説明してください:
Glu ⟶ G6P ΔG° = ?
62.生化学的経路の解糖における重要な反応の1つは、グルコース-6-リン酸(G6P)がフルクトース-6-リン酸(F6P)を生成する反応です:
G6P ⇌ F6P ΔG° = 1.7 kJ
(a)標準的な熱力学的条件下では、この反応は自発的ですか、非自発的ですか?
(b)標準的な熱力学的条件は、G6PとF6Pの濃度が1Mであることを含意していますが、典型的な細胞内では、これらの値に近い値ですらありません。G6PとF6Pの濃度がそれぞれ120μMと28μMのときのΔGを計算し、これらの条件下での順方向反応の自発性について議論してください。温度を37°Cと仮定してください。
63.数値計算をしないで、以下のものについて、温度を上げると反応の自由エネルギー変化が小さくなる(つまり、正の値が小さくなるか、負の値が大きくなる)ものを決定してください。説明してください。
(a)N₂(g) + 3H₂(g) ⟶ 2NH₃(g)
(b)HCl(g) + NH₃(g) ⟶ NH₄Cl(s)
(c)(NH₄)₂Cr₂O₇(s) ⟶ Cr₂O₃(s) + 4H₂O(g) + N₂(g)
(d)2Fe(s) + 3O₂(g) ⟶ Fe₂O₃(s)
64.塩化アンモニウムを水に加えて撹拌すると、それは自発的に溶解し、得られた溶液は冷たく感じます。計算をせずに、この過程のΔG、ΔH、ΔSの符号を推測し、あなたの選択が正当である根拠を示してください。
65.銅の重要な供給源は、銅鉱石(輝銅鉱、硫化銅(I)の一形態)です。加熱すると、Cu₂Sは分解して、以下の反応式で表されるように銅と硫黄を生成します:
Cu₂S(s) ⟶ Cu(s) + S(s)
(a)Cu₂S(s)の分解のΔG°を決定してください。
(b)硫黄と酸素の反応では、二酸化硫黄が唯一の生成物として得られます。この反応を記述する反応式を書き、その過程のΔG°を決定してください。
(c)輝銅鉱からの銅の生成は、Cu₂Sを空気中で焙焼してCuを生成することによって行われます。設問(a)と(b)の反応式を組み合わせて、輝銅鉱の焙焼を記述する反応式を書き、これらの反応を結合させた方が銅の生産にとって効率的なプロセスになる理由を説明してください。
66.以下の化学反応について、酸素の分圧を上げると、ΔGには何が起きるでしょうか(より負になるでしょうか、より正になるでしょうか)?
(a)S(s) + O₂(g) ⟶ SO₂(g)
(b)2SO₂(g) + O₂(g) ⟶ 2SO₃(g)
(c)HgO(s) ⟶ Hg(l) + O₂(g)
解答のヒント
1.反応は自然に起こる傾向があり、外部の源からのエネルギーの継続的な投入がなくても生じます。
3.(a)自発的、(b)非自発的、(c)自発的、(d)非自発的、(e)自発的、(f)自発的
5.プラスチックの酸化は自発的ですが、酸化の速度は非常に遅いです。そのため、プラスチックは反応速度論的に安定しており、比較的長い時間をかけても感知可能なほどに分解することはありません。
7.4つの初期の微視的状態と4つの最終的な微視的状態があります。
\[ ΔS = k \ln \frac{W_{\rm f}}{W_{\rm i}}= 1.38 × 10^{−23}\ {\rm J/K}× \ln\frac{4}{4}= 0\\ \]
9.すべての粒子が片側にある確率は1/32です。この確率は4粒子系の1/8という結果よりも明らかに低いです。私たちが引き出せる結論としては、粒子の数が増えるにつれて、すべての粒子が系の片側だけに留まる確率は急激に減少するということ、そして、たとえば、常温常圧の部屋で気体の分子が片側だけに集まる確率は、部屋の気体分子の数が非常に多いので無視できるということです。
11.初期状態は1つしかありません。最終状態では、A-C、A-D、B-C、またはB-Dのペアにエネルギーが含まれている可能性があります。したがって、最終的に可能な状態は4つです。
\[ ΔS = k \ln \left(\frac{W_{\rm f}}{W_{\rm i}}\right)= 1.38 × 10^{−23}\ {\rm J/K}× \ln\left(\frac{4}{1}\right) = 1.91 × 10^{−23}\ {\rm J/K}\\ \]
13.これらの分子の質量は、それらのエントロピーとは逆の傾向を示すでしょう。観測された傾向は、物理状態に伴うエントロピーのより顕著な変動の結果です。室温では、I₂は固体、Br₂は液体、Cl₂は気体です。
15.(a)C₃H₇OH(l)、なぜならそれはより大きな分子(より複雑で、より質量が大きい)であり、所与の温度では、その運動を記述するようなより多くの微視的状態が利用可能であるからです。(b)C₂H₅OH(g)、なぜなら気体の状態であるからです。(c)2H(g)、エントロピーは示量性であるため、2つのH原子(またはH原子の2モル)は1つの原子(または原子の1モル)の2倍のエントロピーを持っています。
17.(a)負。比較的秩序のある固体が沈殿すると、溶液中で移動できるイオンの数が減少します。(b)負。反応物から生成物では、正味3モルの気体の減少があります。(c)正。反応物から生成物では、正味7モルの気体の増加があります。
19.C₆H₆(l) + 7.5 O₂(g) ⟶3H₂O(g) + 6CO₂(g) 最初は7.5モルの気体があり、最終的には3+6=9モルの気体があります。したがって、この反応の結果としてエントロピーが増加し、ΔSが正であると考えられます。
21.(a)107 J/K、(b)−86.4 J/K、(c)133.2 J/K、(d)118.8 J/K、(e)−326.6 J/K、(f)−171.9 J/K、(g)−7.2 J/K
23.100.6 J/K
25.(a)−198.1 J/K、(b)−348.9 J/K
27.これらのそれぞれの温度ではΔS宇宙 < 0なので、いずれの温度でも融解は自発的ではありません。エントロピーとエンタルピーの与えられた値は、298KでのNaClについてのものです。この問題で用いられている高い温度では、これらは顕著に変化しないと仮定されています。
29.(a)2.86 J/K、(b)24.8 J/K、(c)−113.2 J/K、(d)−24.7 J/K、(e)15.5 J/K、(f)290.0 J/K
31.この反応は室温では非自発的です。400K超ではΔGが負になり、反応は自発的になります。
33.(a)465.1 kJ、非自発的、(b)−106.86 kJ、自発的、(c)−291.9 kJ、自発的、(d)−83.4 kJ、自発的、(e)−406.7 kJ、自発的、(f)−30.0 kJ、自発的
35.(a)標準生成自由エネルギーは-1124.3 kJ/molです。(b)自由エネルギーは状態関数(エンタルピーやエントロピーと同じ)であり、その変化は初期状態と最終状態の間の経路ではなく、初期状態と最終状態にのみ依存するため、この計算は付録Gの値と一致します。
37.(a)この反応は非自発的です、(b)566°C超では、この反応は自発的です。
39.(a)1.5 × 10²kJ、(b)−21.9 kJ、(c)−5.34 kJ、(d)−0.383 kJ、(e)18 kJ、(f)71 kJ
41.(a)K = 41、(b)K = 0.053、(c)K = 6.9 × 10¹³、(d)K = 1.9、(e)K = 0.04
43.以下のそれぞれでは、反応の温度でのΔGの値が与えられていません。したがって、私たちはΔH°とΔSの値からΔGを計算し、ΔG = ΔH° − TΔS°の関係からΔGを計算しなければなりません。(a)K = 1.29、(b)K = 2.51 × 10⁻³、(c)K = 4.83 × 10³、(d)K = 0.219、(e)K = 16.1
45.標準自由エネルギー変化は、ΔG° = −RT lnK = 4.84 kJ/molです。反応物と生成物が標準状態(1 barまたは1 atm)にあるとき、Q = 1です。反応が平衡に向かって進むと、反応は左側に移動し(生成物の量は減少し、反応物の量は増加します):Q < 1、ΔGはゼロに近づくにつれて正の値が小さくなります。平衡では、Q = K、ΔG = 0となります。
47.この反応は287Kよりも高い温度では自発的でしょう。
49.K = 5.35 × 10¹⁵、このプロセスは発熱性です。
51.1.0 × 10⁻⁸atm。これは、記載された条件下での気体の最大圧力です。
53.x = 1.29 × 10⁻⁵atm = PO₂
55.−0.16 kJ
56.(a)22.1 kJ、(b)61.5 kJ/mol
58.90 kJ/mol
60.(a)標準的な熱力学的条件下では、蒸発は非自発的です、(b)Kp = 0.031、(c)水の蒸発は自発的です、(d)PH₂Oは常にKp未満、すなわち0.031 atm未満でなければなりません。0.031 atmは、25°Cで水蒸気で飽和した(または湿度100%の)空気を表します。
62.(a)ΔG° > 0なので非自発的
(b)
\[ ΔG = ΔG ° + RT \ln Q\\ ΔG = 1.7 × 10^3 +\left(8.314 × 310 × \ln\frac{28}{120}\right)= −2.1\ {\rm kJ}\\ \]
F6Pを生成するための順方向の反応は、これらの条件下では自発的です。
64.プロセスが自発的であるため、ΔGは負です。溶液が冷たくなっていると、溶解は吸熱性でなければならないので、ΔHは正です。ΔSは正でなければなりません。なぜなら、これがプロセスを駆動するものであり、それは任意の可溶性イオン化合物の溶解について期待されることだからです。
66.(a)酸素分圧を上げるとQが減少し、ΔGはより負になります。(b)酸素分圧を上げるとQが減少し、ΔGはより負になります。(c)酸素分圧を上げるとQが増加し、ΔGはより正になります。
この訳文は元の本のCreative Commons BY 4.0ライセンスに従って同ライセンスにて公開します。問題がありましたら、可能な限り早く対応いたしますので、ご連絡ください。また、誤訳・不適切な表現等ありましたらご指摘ください。この本は、https://openstax.org/details/books/chemistry-2eで無料でダウンロードできます。