付録B 必須の数学

指数の演算

指数的記数法は、非常に大きな数や非常に小さな数を2つの数の積として表現するために使用されます。その積の最初の数である数値項は、通常、1以上10未満の数です。積の2番目の数である指数項は、10に指数を付けて書きます。指数的記数法のいくつかの例としては、以下のようなものがあります:

\[ \begin{eqnarray} 1000 &=& 1 × 10^3\\ 100 &=& 1 × 10^2\\ 10 &=& 1 × 10^1\\ 1 &=& 1 × 10^0\\ 0.1 &=& 1 × 10^{-1}\\ 0.001 &=& 1 × 10^{-3}\\ 2386 &=& 2.386 × 1000 = 2.386 × 10^3\\ 0.123 &=& 1.23 × 0.1 = 1.23 × 10^{-1}\\ \end{eqnarray} \]

10の累乗(指数)は、桁数を与えるために小数点の位置を何桁ずらしたかに相当します。指数法は、すべての大きな数字と非常に小さな数字を表記するのに特に便利な方法です。たとえば、1,230,000,000 = 1.23 × 10⁹であり、0.00000000036 = 3.6 × 10⁻¹⁰です。

指数の足し算

すべての数字を同じ10の累乗に変換し、数値項の数字を足し、必要に応じて指数項を調整することにより数値項を1から10の間の数に戻します。

例題B1 指数の足し算

5.00 × 10⁻⁵と3.00 × 10⁻³を足してください。

解法

\[ 3.00 × 10^{−3} = 300 × 10^{−5}\\ (5.00 × 10^{−5}) + (300 × 10^{−5}) = 305 × 10^{−5} = 3.05 × 10^{−3} \]

指数の引き算

すべての数字を同じ10の累乗に変換し、数値項の差を取り、必要に応じて指数項を調整することにより数値項を1から10の間の数に戻します。

例題B2 指数の引き算

5.0 × 10⁻⁶から4.0 × 10⁻⁷を引いてください。

解法

\[ 4.0 × 10^{−7} = 0.40 × 10^{−6}\\ (5.0 × 10^{−6}) − (0.40 × 10^{−6}) = 4.6 × 10^{−6} \]

指数の掛け算

数値項を通常の方法で掛け、指数項の指数を足します。

例題B3 指数の掛け算

4.2 × 10⁻⁸に2.0 × 10³を掛けてください。

解法

\[ (4.2 × 10^{−8})× (2.0 × 10^{3}) = (4.2 × 2.0)× 10^{(−8) + (+3)} = 8.4 × 10^{−5} \]

指数の割り算

分子の数値項を分母の数値項で割り、指数項の指数を引きます。

例題B4 指数の割り算

3.6 × 10⁵を6.0 × 10⁻⁴で割ってください。

解法

\[ \frac{3.6 × 10^{−5}}{6.0 × 10^{−4}}=\left(\frac{3.6}{6.0}\right)× 10^{(−5) − (−4)} = 0.60 × 10^{−1} = 6.0 × 10^{−2} \]

指数の二乗

数値項を通常の方法で二乗し、指数項の指数に2を掛けます。

例題B5 指数の二乗

4.0×10⁻⁶を二乗してください。

解法

\[ (4.0 × 10^{−6})^2 = 4 × 4 × 10^{2 × (−6)} = 16 × 10^{−12} = 1.6 × 10^{−11} \]

指数の三乗

数値項を通常の方法で三乗し、指数項の指数に3を掛けます。

例題B6 指数の三乗

2×10⁴を三乗してください。

解法

\[ (2 × 10^4)^3 = 2 × 2 × 2 × 10^{3 × 4} = 8 × 10^{12} \]

指数の平方根を取る

必要に応じて、10の累乗が2で割り切れるように、指数項を減らしたり増やしたりしてください。数値項の平方根を取り、指数項を2で割ってください。

例題B7 指数の平方根を求める

1.6 × 10⁻⁷の平方根を求めてください。

解法

\[ 1.6 × 10^{−7} = 16 × 10^{−8}\\ \sqrt{16 × 10^{−8}} = \sqrt{16} × \sqrt{10^{−8}} = \sqrt{16} × 10^{−\frac{8}{2}}= 4.0 × 10^{−4} \]

有効数字

ある養蜂家が、52万5341匹のハチを飼っていると報告しています。この数の最後の3つの数字は明らかに不正確です。なぜなら、養蜂家がハチを数えている間に、死んだハチもいれば羽化したハチもいるからです。そのため、ハチの正確な数を決定することは非常に困難です。もしこの養蜂家が52万5000匹と報告していれば、もっと理にかなったものであったでしょう。言い換えれば、最後の3つの数字は、小数点の位置を決める以外には意味がありません(有効ではありません)。それらの正確な値はこの状況では何の意味もありません。量を報告する際には、測定の正確度が保証される範囲内の有効数字のみを使用します。

有効数字の重要性は、基本的な計算への応用にあります。足し算と引き算では、和または差は、計算に使用される数の中で最も確かさが低い数(以下の例題では下線で示されています)の小数点以下の桁と同じだけの小数点以下の桁を含むべきです。

例題B8 有効数字を用いた足し算と引き算

4.383gと0.0023gを足してください。

解法

\[ \begin{array}{ll} & \rm 4.383\ g\\ + & \rm 0.0023\ g\\ \hline & \rm 4.385\ g\\ \end{array} \]

掛け算と割り算では、積または商は、最も小さい有効数字を含む要素の桁数よりも大きな桁数が含まれてはなりません。

例題B9 有効数字を用いた掛け算と割り算

0.6238に6.6を掛けてください。

解法

\[ 0.6238 × 6.6 = 4.1 \]

数値を丸める場合、保持される桁の後に5より大きい数値が続く場合は、保持される桁を1だけ増やします(「切り上げ」)。保持される桁に続く数値が5未満の場合は、保持される桁を変更しないでください(「切り下げ」)。保持される桁の後に5が続く場合、保持される桁が奇数の場合は切り上げ、保持される桁が偶数の場合は切り下げます(丸めた後は、保持される桁は常に偶数になります)。

対数と指数の使用

ある数の常用対数(log)とは、10に累乗するとその数に等しくなるような指数のことです。たとえば、100の常用対数は2です。なぜなら、100 と等しくなるためには10を2乗しなければならないからです。その他の例を以下に示します。

表B1

60の常用対数は何でしょうか?60は10と100の間にあり、10と100はそれぞれ1と2の対数を持つので、60の常用対数は1.7782となります。つまり、

\[ 60 = 10^{1.7782} \]

1未満の数の常用対数は負の値を持ちます。0.03918の対数は-1.4069、つまり

\[ 0.03918 = 10^{−1.4069} = \frac{1}{10^{1.4069}} \]

ある数の常用対数を求めるには、電卓のlogボタンを使用します。ある数をその対数から計算するには、対数の逆の対数を取る、つまり10^x を計算します(ここで x はその数の対数です)。

ある数の自然対数(ln)とは、eに累乗するとその数に等しくなるような指数のことです。eは定数2.7182818です。たとえば、10の自然対数は2.303です。つまり、

\[ 10 = e^{2.303} = 2.7182818^{2.303} \]

ある数の自然対数を求めるには、電卓のlnボタンを使用します。ある数をその自然対数から計算するには、自然対数を入力し、その自然対数の逆の自然対数を取る、つまりe^xを計算します(ここでxはその数の自然対数です)。

対数は指数なので、対数を含む演算は指数を含む演算と同じルールに従います。

2つの数の積の対数は、2つの数の対数の和です。 \[ \log xy = \log x + \log y、および\ln xy = \ln x + \ln y \]
2つの数の割り算から得られる数の対数は、2つの数の対数の差です。 \[ \log \frac{x}{y} = \log x − \log y、および\ln \frac{x}{y} = \ln x − \ln y \]
ある指数で累乗した数の対数は、その指数とその数の対数との積です。 \[ \log x^n = n \log x、および\ln x^n = n \ln x \]

二次方程式の解法

この形式の数学的な関数は、2次多項式、またはより一般的には2次関数として知られています。

\[ ax^2 + bx + c = 0 \]

任意の二次方程式の解または根は、以下の公式を用いて計算することができます:

\[ x = \frac{−b ± \sqrt{b^2 − 4ac}}{2a} \]

例題B10 二次方程式を解く

2次方程式3x² + 13x - 10 = 0を解いてください。

解法

公式の中に値 a = 3、b = 13、c = -10 を代入すると、私たちは以下を得ます

\[ x = \frac{−13 ± \sqrt{(13)^2 − 4 × 3 × (−10)}}{2 × 3}\\ x =\frac{−13 ± \sqrt{169 + 120}}{6}=\frac{−13 ± \sqrt{289}}{6}=\frac{−13 ± 17}{6} \]

そのため、2つの根は

\[ x =\frac{−13 + 17}{6}=\frac{2}{3}\\ および\\ x =\frac{−13 − 17}{6}= −5 \]

物理的データに基づいて構築された二次方程式は常に実根を持ち、これらの実根のうち、正の値を持つものだけが重要であることがしばしばあります。

二次元(x-y)グラフ

ある系の任意の2つの性質の間の関係性は、2次元データプロットによって図的に表現することができます。そのようなグラフは2つの軸を持っています:独立変数、すなわちその値が制御されているような変数(x)に対応する横軸と、従属変数、すなわちその値が観測または測定されるような変数(y)に対応する縦軸です。

yの値がxの関数として変化している場合(すなわち、異なるxの値が異なるyの値に対応している場合)、この変化のグラフをプロットまたは描画することができます。このグラフは、(x,y)データ対についての特定の値を使用することにより作成することができます。

例題B11 yのxに対する従属性をグラフ化する

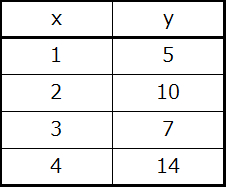
この表には、以下の点が記載されています:(1,5)、(2,10)、(3,7)、および(4,14)。これらの点のそれぞれをグラフ上にプロットしてつなげることにより、yのxに対する従属性のグラフ表示を生成することができます。

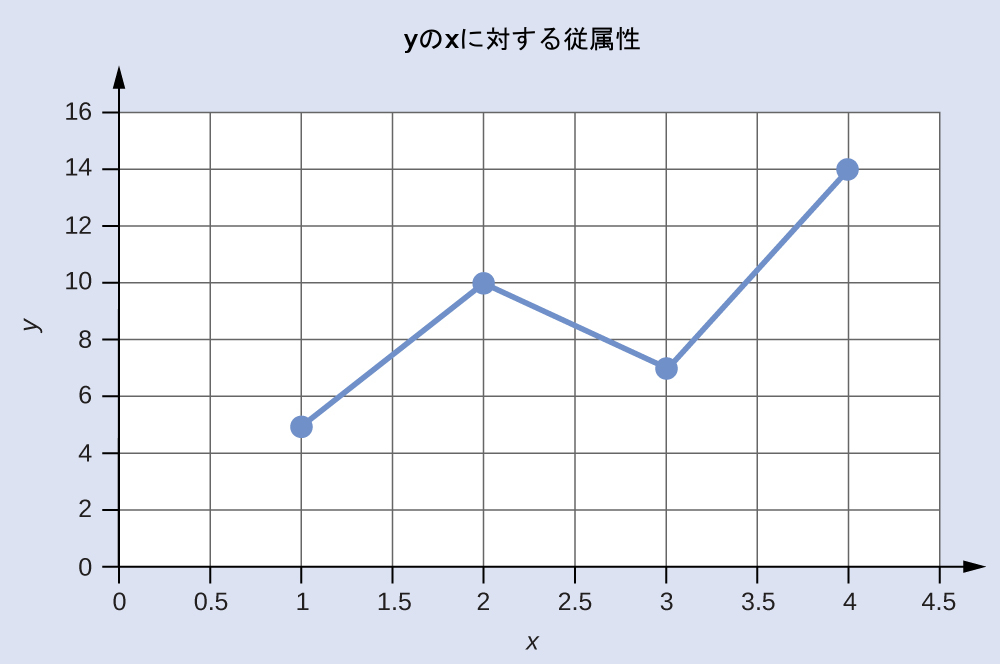
もしy のxに対する従属性を記述する関数が既知であれば、それを使用してx,yのデータ対を計算し、その後にそれらをプロットすることができます。

例題B12 データ対をプロットする

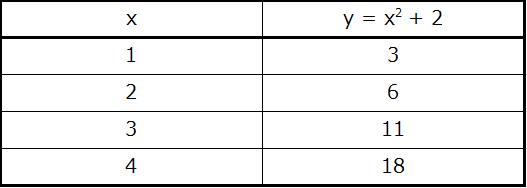
もし私たちがy = x² + 2 ということを知っているならば、私たちはいくつかの(x,y)値の表を作成することができ、その後でここに示されたデータに基づいて線をプロットすることができます。

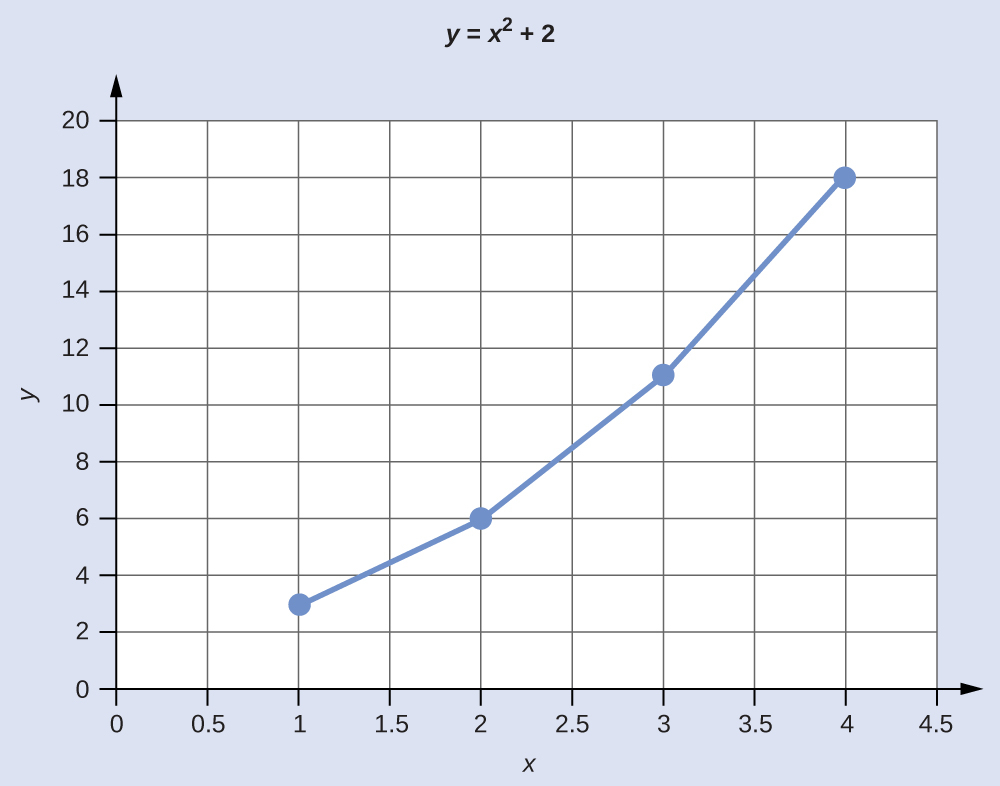
この訳文は元の本のCreative Commons BY 4.0ライセンスに従って同ライセンスにて公開します。問題がありましたら、可能な限り早く対応いたしますので、ご連絡ください。また、誤訳・不適切な表現等ありましたらご指摘ください。この本は、https://openstax.org/details/books/chemistry-2eで無料でダウンロードできます。