第10章 液体と固体
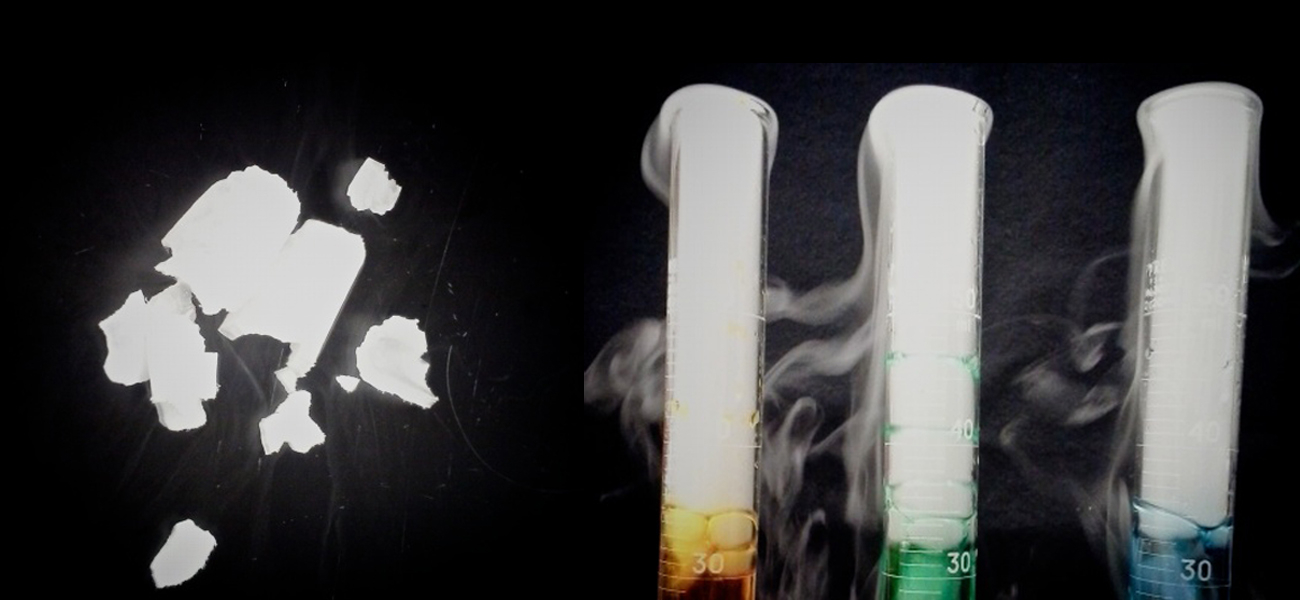
図10.1 | 固体の二酸化炭素(「ドライアイス」、左側)は液体(右側)の中に入れると勢いよく昇華し、液体を冷却し、シリンダーの上部に水の濃密な霧を発生させます。(credit: modification of work by Paul Flowers)
この章の概要
10.1 分子間力
10.2 液体の性質
10.3 相転移
10.4 相図
10.5 物質の固体状態
10.6 結晶性固体の格子構造
はじめに
気相においては原子や分子の間には大きな距離があり、それに対応して原子や分子の間には大きな相互作用がないため、化学的な同一性に関係なく、すべての気体に共通する多くの物理的性質を簡単に記述することができます。気体の章の最後の節で記述したように、この状況は高圧と低温(原子や分子がより大きな程度で相互作用することを可能にする条件)では変化します。液体と固体の状態では、これらの相互作用は非常に強く、物質の化学的同一性に依存する多くの物理的性質を決定する上で重要な役割を果たしています。本章では、これらの相互作用の性質と、液相および固相のさまざまな物理的性質に対するそれらの相互作用の影響について検討します。
10.1 分子間力
この節が終わるまでに、あなたは次のことができるようになります:
•凝縮相の原子または分子間で可能な分子間力の種類を記述する(分散力、双極子-双極子引力、水素結合)
•構造に基づいて、特定の分子が経験する分子間力の種類を特定する
•物質内に存在する分子間力と、その物理的状態の変化に関連している温度との関係を説明する
気体状の物質の場合と同様に、固体や液体の振る舞いを説明するために、分子運動論を用いることがあります。以下の記述では、粒子という用語は、原子、分子、またはイオンに言及するために使用されます。これらの粒子が分子、原子、またはイオンであるかどうかにかかわらず、物質の粒子間の引力を指すために、「分子間引力」というよく使われる言葉を使用することに注意してください。
固体状、液体状、気体状の物質における分子レベルの環境について、この2つの側面を考えてみましょう:
固体中の粒子は緊密にまとまっていて、しばしば規則的なパターンで配置されています。液体の場合、粒子は近くにありますが、規則的な配置を持ちません。気体の場合、粒子は遠くに離れており、規則的な配置を持ちません。
固体中の粒子は固定された位置で振動しており、一般的にはお互いの位置関係が動くことはありません。液体中の粒子は、互いにすれ違うように移動しますが、基本的には一定の接触状態を保ちます。気体中の粒子は、衝突するときを除いて、互いに独立して移動します。
固体、液体、または気体の性質の違いは、それぞれの相を構成する原子、分子、またはイオン間の引力の強さを反映しています。ある物質が存在する相は、その分子間力(IMF)と分子の運動エネルギー(KE)の相対的な度合いに依存します。IMFとは、この節で詳しく説明するように、静電現象に起因して物質の原子や分子の間に存在することのあるさまざまな引力のことです。これらの力は粒子を互いに近づけて保持するのに役立つ一方で、粒子のKEは、引力を克服するために必要なエネルギーを提供し、その結果、粒子間の距離を増大させます。図10.2は、所与の物質の温度、つまり平均KEを変化させることによって物理状態がどのように変化するかを示しています。
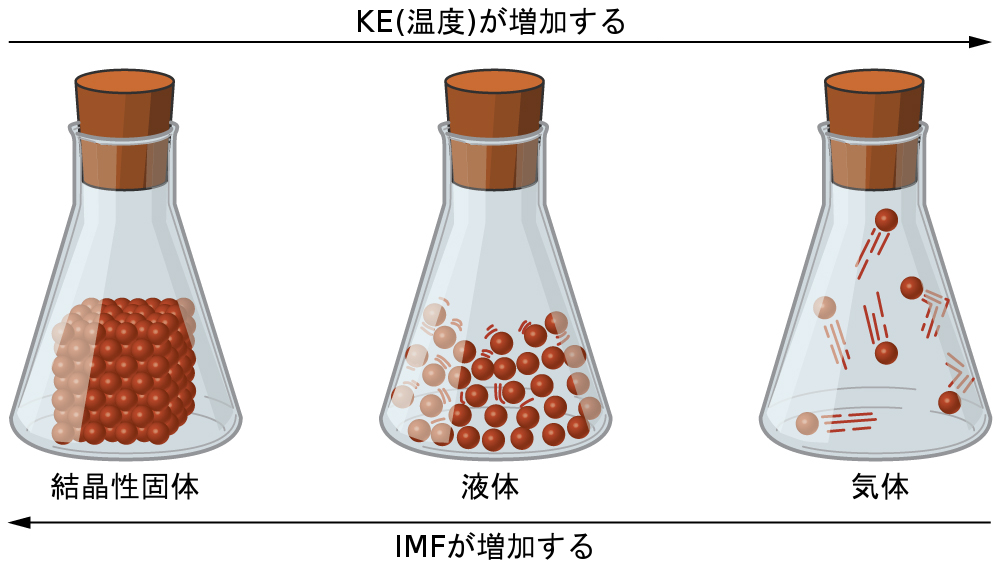
図10.2 | 物質の固体、液体、気体の状態の間の遷移は、温度や圧力の条件が分子間力の変化に有利に働く場合に発生します。(注:気相中の粒子間の空間は図示されたものよりもはるかに大きいです。)
この図に描かれているプロセスの一例として、水のサンプルを考えてみましょう。気体の水が十分に冷却されると、H₂O分子同士が接触したときに、H₂O分子間の引力でまとまって保持されるようになります。気体は凝縮して液体のH₂Oができます。たとえば、図10.3に示されるように、空気中の水蒸気が冷たいグラスによって冷やされると、冷たいグラスの外側に液体の水ができます。

図10.3 | 凝縮は空気中の水蒸気が十分に冷却されて液体の水を形成するときに生じます(たとえば、(a)冷たい飲み物のグラスの外側や、(b)霧の形態で)。(credit a: modification of work by Jenny Downing; credit b: modification of work by Cory Zanker)
また、温度が高すぎなければ、圧縮することによって多くの気体を液化することもできます。圧力が高くなると、気体の分子同士が近づき、分子間の引力がその分子のKEに比べて強くなります。その結果、その分子は液体を形成します。ブタン(C₄H₁₀)は使い捨てライターに使用される燃料であり、標準的な温度と圧力では気体です。図10.4に示されるように、ライターの燃料室内では、ブタンは凝縮して液体状態になるような圧力にまで圧縮されています。

図10.4 | 使い捨てライターの燃料室内では気体のブタンが圧縮され、凝縮して液体になっています。(credit: modification of work by “Sam-Cat”/Flickr)
最後に、液体の温度が十分に低くなったり、液体の圧力が十分に高くなったりすると、液体の分子はもはや分子間のIMFを克服するのに十分なKEを持たなくなり、固体が形成されます。これらの状態変化や他の状態変化(相転移)については、この章の後の節で詳しく議論します。
学習へのリンク
物質の状態、相転移、分子間力に関するインタラクティブなシミュレーション(http://openstaxcollege.org/l/16phetvisual)にアクセスしてください。このシミュレーションは、この章を通じて紹介する概念を視覚化するのに役立ちます。
分子の間の力
適切な条件下では、すべての気体分子間の引力により、液体または固体が形成されるようになるでしょう。これは分子内力によるものではなく、分子間力によるものです。分子内力とは、分子をまとめて保持する分子内の力で、たとえば原子間の結合などがあります。分子間力は分子の間の引力であり、物質の物理的性質の多くを決定します。図10.5は、これらの異なる分子の力を示しています。これらの引力の強さは大きく異なりますが、通常、小さな分子の間のIMFは、分子内で原子を結合させる分子内力に比べて弱いものです。たとえば、1モルの液体HClのIMFを克服し、気体状のHClに変換するには、わずか約17キロジュールしか必要としません。しかしながら、1モルのHCl中の水素原子と塩素原子の間の共有結合を破壊するには、430キロジュール(約25倍のエネルギー)が必要です。
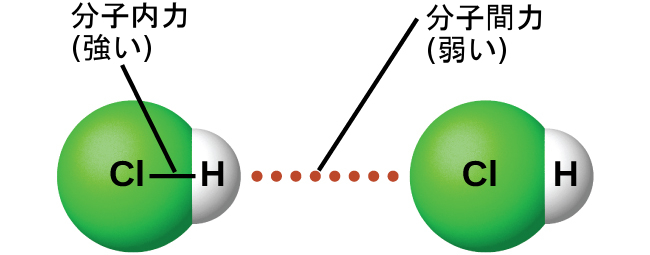
図10.5 | 分子内力が分子をまとめて保持します。分子間力は複数の分子を一緒に保持し、物質の性質の多くを決定します。
中性の原子と分子の間のすべての引力はファン・デル・ワールス力として知られていますが、それらは通常、より非公式に分子間引力と呼ばれています。私たちは、この節の次の3つの項で、さまざまな種類のIMFについて考えていきます。
分散力
3つのファン・デル・ワールス力のうちの1つは、物質を構成する原子や分子の性質に関係なく、すべての凝縮相に存在しています。この引力は、1928年に初めてこの力を説明したドイツ生まれのアメリカ人物理学者フリッツ・ロンドンにちなんで、ロンドン分散力と呼ばれています。この力は、しばしば単純に分散力と呼ばれることがあります。原子や分子の電子は常に運動をしているため(あるいは、別の言い方では、電子の位置が量子力学的に変動するため)、時間の中のいかなる瞬間であっても、原子や分子の電子が非対称的に分布していると、一時的で瞬間的な双極子を発生させることがあります。この双極子が存在すると、隣接する原子や分子の電子が歪み、誘起双極子が発生します。したがって、これら2つの急速に変動する一時的な双極子は、種の間に比較的弱い静電引力、いわゆる分散力(図10.6に示されているような)をもたらします。
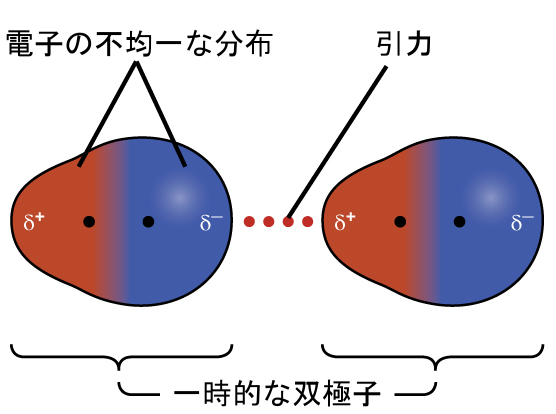
図10.6 | 分散力は一時的な双極子の形成に起因しており、ここでは2つの非極性二原子分子の例を示しています。
異なる分子の原子間で発生する分散力は、2つの分子を互いに引きつけることができます。しかしながら、この力は比較的弱く、分子が非常に近くにある場合にのみ顕著になります。大きくて重い原子や分子ほど、小さくて軽い原子や分子よりも強い分散力を示します。F₂とCl₂は室温では気体であり(弱い引力を反映しています)、Br₂は液体であり、I₂は固体です(より強い引力を反映しています)。表10.1に示されるように、ハロゲンについて観測される融点と沸点の傾向は、この効果を明確に示しています。
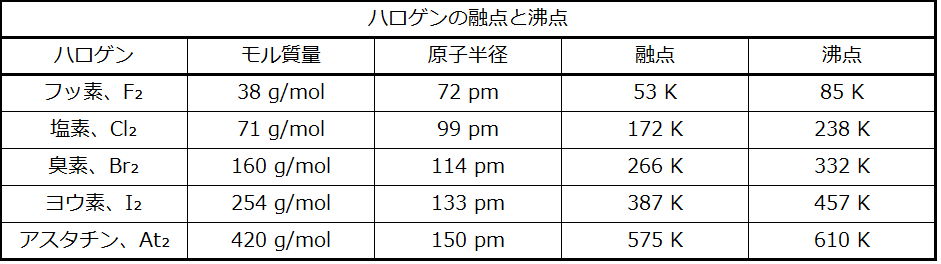
表10.1
原子/分子サイズの増加に伴う融点と沸点の上昇は、分散力の強さが物質中の原子または分子の電子構造によってどのように影響を受けるかを考慮することによって理屈づけられるかもしれません。大きい原子では、価電子は平均して、小さい原子よりも原子核から離れています。そのため、原子の価電子はあまり強固に保持されておらず、引力を生み出す一時的な双極子を形成しやすくなっています。分子の電荷分布(その電子の雲)が、別の静電電荷(たとえば、近くにあるイオンや極性分子)によってどれだけ容易に歪められるか、あるいは歪めるのがどれだけ困難かを示す尺度は、分極率として知られています。歪みやすい電荷の雲を持つ分子は非常に分極しやすいと言われ、大きな分散力を持ちます。歪みにくい電荷の雲を持つ分子は分極しにくく、小さな分散力を持ちます。
例題10.1 ロンドン力とその効果
以下の第14族元素と水素との化合物を、沸点の低いものから高いものまで順に並べてください:CH₄、SiH₄、GeH₄、SnH₄。あなたの推論を説明してください。
解法
化学結合と分子の幾何構造に関する章で得た技能を適用すると、これらの化合物はすべて非極性であると予測されるため、分散力だけが発生するでしょう:分子が小さいほど分極しにくく、分散力が弱くなります。分子が大きいほど分散力が大きくなります。CH₄、SiH₄、GeH₄、SnH₄のモル質量は、それぞれ約16g/mol、32g/mol、77g/mol、123g/molです。したがって、CH₄が最も低い沸点を持ち、SnH₄が最も高い沸点を持つと予想されます。沸点の低いほうから高いほうへと順に、CH₄ < SiH₄ < GeH₄ < SnH₄となると予想されます。
これらの化合物の実際の沸点と第14族元素の周期のグラフは、この予測が正しいことを示しています:
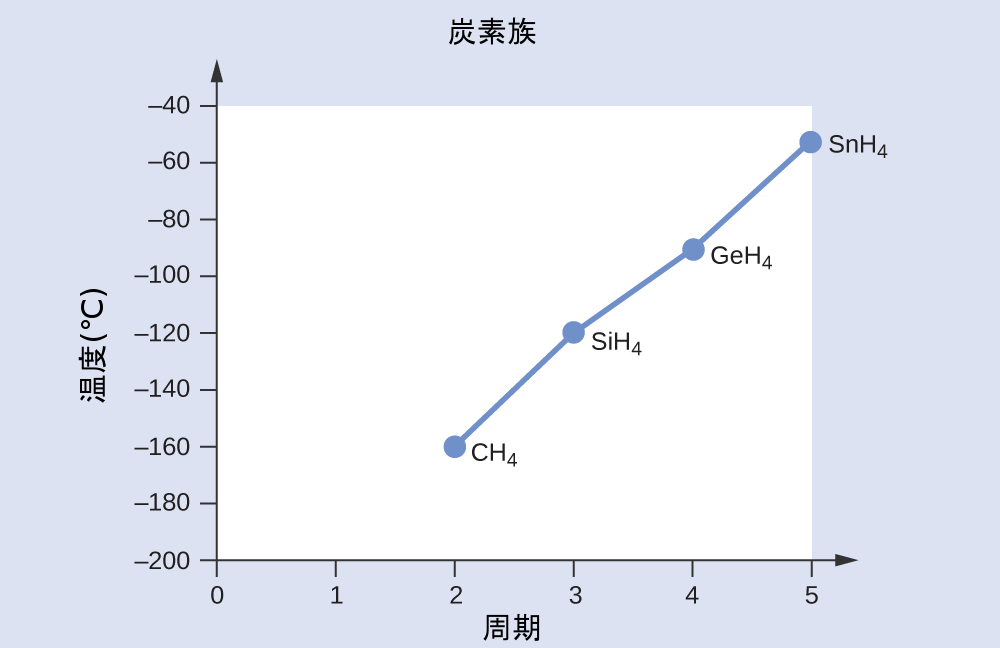
学習内容の確認
以下の炭化水素を沸点の低いものから高いものまで順に並べてください:C₂H₆、C₃H₈、およびC₄H₁₀
解答:C₂H₆ < C₃H₈ < C₄H₁₀。これらの化合物はすべて非極性で、ロンドン分散力のみを持ちます:分子が大きいほど分散力が大きく、沸点が高くなります。したがって、沸点の低いものから高いものへの順序は、C₂H₆ < C₃H₈ < C₄H₁₀となります。
分子の形状もまた分子間の分散力の大きさに影響を与えます。たとえば、異性体である n-ペンタン、イソペンタン、ネオペンタン(図10.7に示されています)の沸点はそれぞれ 36 °C、27 °C、9.5 °Cです。これらの化合物は同じ化学式C₅H₁₂の分子で構成されているにもかかわらず、その沸点の違いは液相における分散力の違い(n-ペンタンが最も大きく、ネオペンタンが最も小さい)を示唆しています。n-ペンタンの細長い形状は、分子間の接触に利用できる表面積を大きくし、それに応じてより強い分散力をもたらします。イソペンタンのよりコンパクトな形状によって、分子間の接触に利用できる表面積が小さくなり、その結果、分散力が弱くなります。ネオペンタン分子は、3つの中で最もコンパクトなものであり、分子間の接触のために利用可能な表面積が最も少なく、したがって、最も弱い分散力を提供します。この振る舞いは、VELCROブランドの面ファスナー(マジックテープ)の布片の間に形成されるであろう接着に類似しています:布片の接触の面積が大きいほど、接着が強くなります。
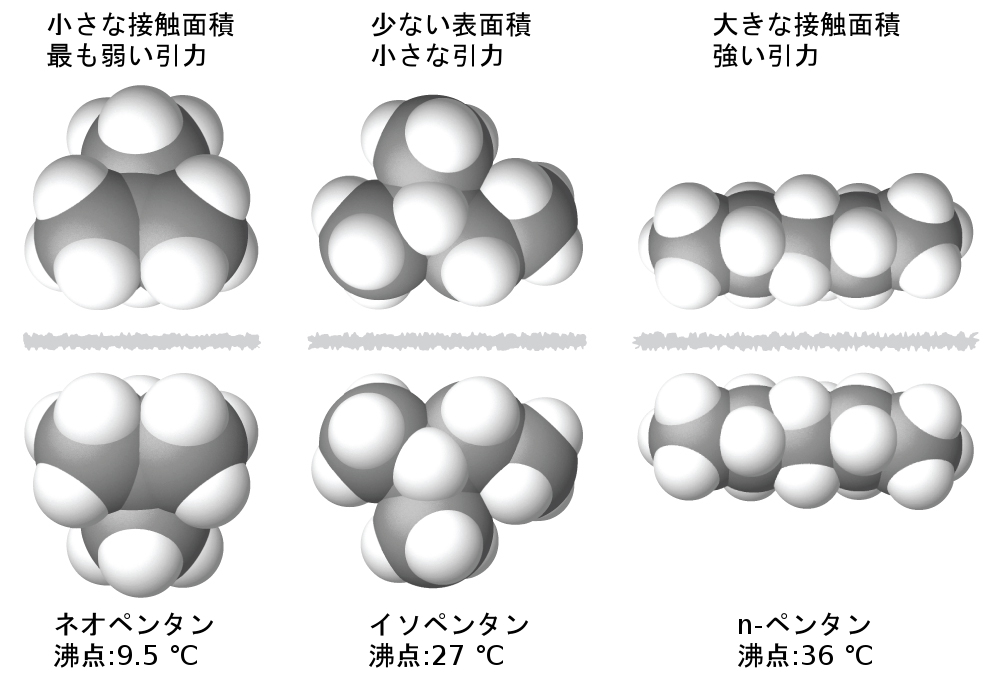
図10.7 | ペンタン異性体の沸点によって示されるように、分散力の強さは分子間の接触面積が大きいほど大きくなります。
日常生活の中の化学
ヤモリと分子間力
ヤモリは、ほとんどの表面に付着する驚くべき能力を持っています。ヤモリは、滑らかな壁を素早く駆け上がったり、とっかかりのない天井を横切ったりすることができ、しかも足の指に吸盤や粘着性のある物質を持たずにこれを行うことができます。そして、ヤモリは、表面に沿って歩いていくときには簡単にその足を持ち上げることができますが、あなたが摘まみ上げようとすると、それは表面に付着します。ヤモリ(クモや他の昆虫もそうですが)は、どうしてこのようなことができるのでしょうか?この現象は何百年にもわたって研究されてきましたが、ヤモリの足がこのような振る舞いをするのを可能にするプロセスの詳細を科学者が明らかにしたのは、最近になってようやくのことでした。
ヤモリの足の指は、剛毛として知られる何十万本もの小さな毛によって覆われており、それぞれの剛毛は、ヘラ状構造と呼ばれる何百本もの小さな平らな三角形の先端に枝分かれしています。図10.8に示されるように、剛毛にある膨大な数のヘラ状構造によって、ヤモリは表面に付着するための大きな表面積を持つことになります。2000年、複数機関の合同のヤモリ研究チームを率いるケラー・オータムは、極性の二酸化ケイ素と非極性のガリウムヒ素の両方に、ヤモリが同等によく付着することを発見しました。これにより、ヤモリが表面に付着するのは、隣接する分子間の一時的で同期した電荷分布から生じる弱い分子間引力、すなわち分散力のおかげであることが証明されました。分散力は非常に弱いものですが、何百万ものヘラ状構造の合計の引力は、ヤモリの体重の何倍もの重さを支えるのに十分なほど大きいものです。
2014年、2人の科学者が、ヤモリが「粘着性のある」状態から「粘着性のない」状態へと急速に移行することのできる方法を説明するモデルを開発しました。オレゴン州立大学のアレックス・グレイニーとコンコン・フーは、ヤモリがそのヘラ状構造と表面との間の角度を変えることによってこれを達成することができる方法を説明しました。通常は粘着性でないヤモリの足は、小さな剪断力を加えると粘着性になります。足の指を丸めたり伸ばしたりすることで、ヤモリは表面にくっついたりくっつかなかったりを交互に繰り返すことができ、それにより簡単に移動することができるのです。今後の研究により、より良い接着剤や他の応用などの開発につながるかもしれません。

図10.8 | ヤモリの足の指には、多数の小さな毛(剛毛)があり、それらは多くの三角形の先端(ヘラ状構造)に枝分かれしています。ヤモリが表面に付着するのは、表面とヤモリの何百万ものヘラ状構造との間のファン・デル・ワールス引力によるものです。このヘラ状構造の表面への接触の仕方を変えることによって、ヤモリはその粘着性を「オン」と「オフ」に変えることができます。(credit photo: modification of work by “JC*+A!”/Flickr)
学習へのリンク
このビデオ (http://openstaxcollege.org/l/16kellaraut) を見て、ファン・デル・ワールス力がヤモリのしがみついたり、登ったりする能力の原因であることを明らかにしたケラー・オータムの研究についてさらに詳しく学んでください。
双極子-双極子引力
化学結合と分子の幾何構造の章から、極性分子は分子の片側に部分的な正の電荷を持ち、反対側に部分的な負の電荷を持っていること(双極子と呼ばれる電荷の分離)を思い出してください。塩化水素(HCl)のような極性分子を考えてみましょう。HCl分子では、電気陰性度の高いCl原子が部分的に負の電荷を帯びる一方で、電気陰性度の低いH原子が部分的に正の電荷を帯びます。HCl分子間の引力は、あるHCl分子の正の端部と別のHCl分子の負の端部との間の引力によって生じます。この引力は双極子-双極子引力と呼ばれます。これは、図10.9に示されるように、ある極性分子の部分的に正の端部と別の極性分子の部分的に負の端部との間の静電力です。
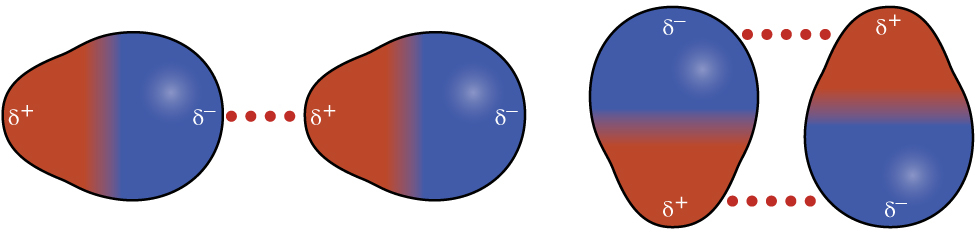
図10.9 | この図は、HClのような極性分子において、ある分子の部分的に負の端部と別の分子の部分的に正の端部との間の引力を可能にする2つの配置を示しています。
双極子-双極子引力の効果は、私たちがHCl分子の性質と非極性のF₂分子の性質とを比較するときに明らかになります。HClもF₂も同じ数の原子で構成されており、分子量はほぼ同じです。150Kの温度では、両方の物質の分子は同じ平均KEを持つことになるでしょう。しかしながら、HCl分子間の双極子-双極子引力は、HCl分子が「くっついて」液体を形成するのに十分であるのに対し、非極性のF₂分子間の比較的弱い分散力はそこまで大きくはないため、この温度ではこの物質は気体状になります。HClの標準沸点(188 K)がF₂(85 K)に比べて高いのは、HCl分子間の双極子-双極子引力の強さが非極性のF₂分子間の引力に比べて大きいことを反映しています。沸点や凝固点、蒸発や融解のエンタルピーなどの値は、異なる物質内に存在するIMFの引力の相対的な強さの指標としてしばしば使用されます。
例題10.2 双極子-双極子力とその効果
N₂とCOのどちらのほうが沸点が高いかを予測してください。あなたの推論を説明してください。
解法
COとN₂はともに約28amuの質量を持つ二原子分子であり、似たようなロンドン分散力がかかっています。COは極性分子であるため、それは双極子-双極子引力を示します。N₂は非極性分子であるため、その分子は双極子-双極子引力を示すことができません。CO分子間の双極子-双極子引力は、非極性のN₂分子間の分散力よりも比較的に強いので、COの方が沸点が高いと予想されます。
学習内容の確認
IClとBr₂のどちらのほうが沸点が高いかを予測してください。あなたの推論を説明してください。
解答:IClです。IClとBr₂は似たような質量を有しているため(~160amu)、似たようなロンドン分散力がかかっています。IClは極性であるため双極子-双極子引力を示し、Br₂は非極性であるため双極子-双極子引力を示しません。比較的強い双極子-双極子引力を克服するには多くのエネルギーを必要とするため、IClの方が沸点が高くなるでしょう。
水素結合
フッ化ニトロシル(ONF、分子量49amu)は室温で気体です。水 (H₂O、分子量18amu) は、分子量が低いにもかかわらず液体です。明らかに、私たちはこの2つの化合物の違いを分散力のせいにすることはできません。両方の分子はほぼ同じ形状をしており、ONFの方が重くて大きな分子です。したがって、それはより大きな分散力がかかることが予想されます。さらに、私たちは、この沸点の違いを分子の双極子モーメントの違いに帰することもできません。どちらの分子も極性を持っており、同等の双極子モーメントを示します。沸点の差が大きいのは、ある分子がフッ素、酸素、または窒素(最も電気的に陰性な3つの元素)に結合した水素原子を含む場合に、特に強い双極子-双極子引力が発生することがあるためです。H原子の電気陰性度(2.1)と、それが結合している原子の電気陰性度(F原子が4.0、O原子が3.5、またはN原子が3.0)の間の非常に大きな違いは、H原子の非常に小さなサイズとF原子、O原子、またはN原子の比較的小さなサイズとあいまって、これらの原子における高度に集中した部分電荷へとつながります。F-H、O-H、またはN-Hの部位を持つ分子は、近くの分子にある似たような部位に非常に強く引きつけられます。この特に強い種類の双極子-双極子引力は水素結合と呼ばれます。水素結合の例としては HF⋯HF、H₂O⋯HOH、H₃N⋯HNH₂などがあります(水素結合は点々で表示されています)。図10.10は水分子間の水素結合を示しています。
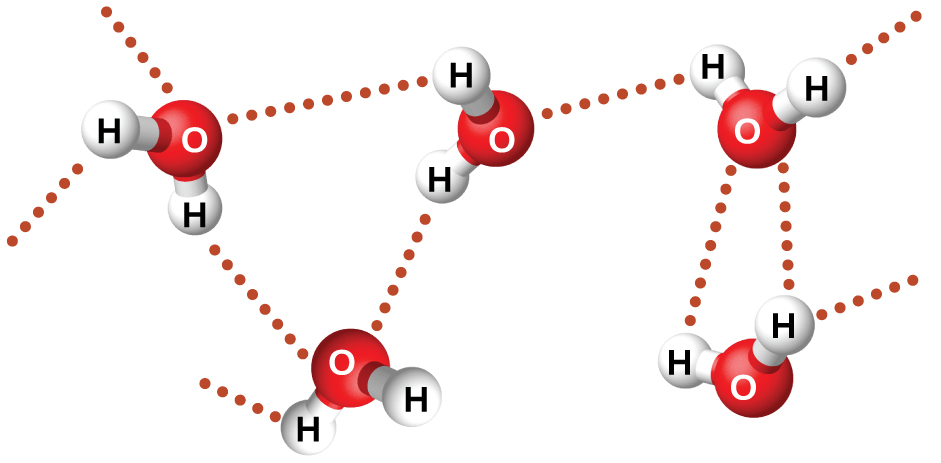
図10.10 | 水分子は、近くの水分子との間で複数の水素結合相互作用をしています。
「結合」という言葉を使ってはいますが、水素結合は分子間の引力であって、分子内の引力(共有結合)ではないことを心に留めておいてください。水素結合は、共有結合よりもはるかに弱く、わずか約5~10%の強さですが、一般的に他の双極子-双極子引力や分散力よりもはるかに強いです。
水素結合は、凝縮相(液体や固体)の性質に顕著な影響を与えます。たとえば、第15族(NH₃、PH₃、AsH₃、SbH₃)、第16族(H₂O、H₂S、H₂Se、H₂Te)、第17族(HF、HCl、HBr、HI)の二元水素化物の沸点の傾向を考えてみましょう。図10.11は、それぞれの族の最も重い3つの水素化物の沸点をプロットしたものです。これらの族のいずれかに沿って下に進むにつれて、分子の極性はわずかに減少する一方で、分子の大きさは大幅に増加します。どんどんと強くなる分散力の効果は、どんどんと弱くなる双極子-双極子引力の効果を圧倒し、沸点は着実に上昇していることが見て取れます。
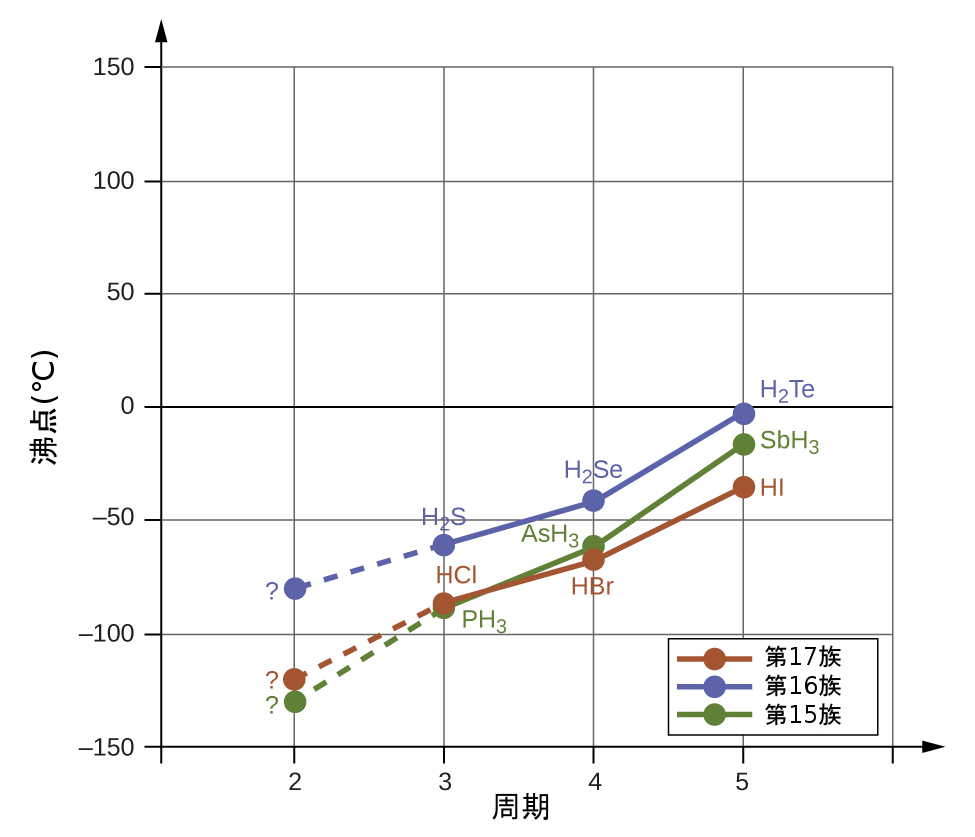
図10.11 | 第15、16、17族の水素化物では、第3、4、5周期の元素の分子量の増加に伴い、それぞれの族の化合物の沸点が増加しています。
もし私たちがこの傾向を利用して、それぞれの族で最も軽い水素化物の沸点を予測すると、NH₃は約-120 °C、H₂Oは約-80 °C、HFは約-110 °C で沸騰すると予想するでしょう。しかしながら、私たちがこれらの化合物の沸点を測定してみると、図10.12に示されるように、傾向によって予測されるものよりも劇的に高いことがわかります。私たちが単純に予測したものと現実のものとが大きく異なることは、水素結合の強さについての説得的な証拠を提供してくれます。
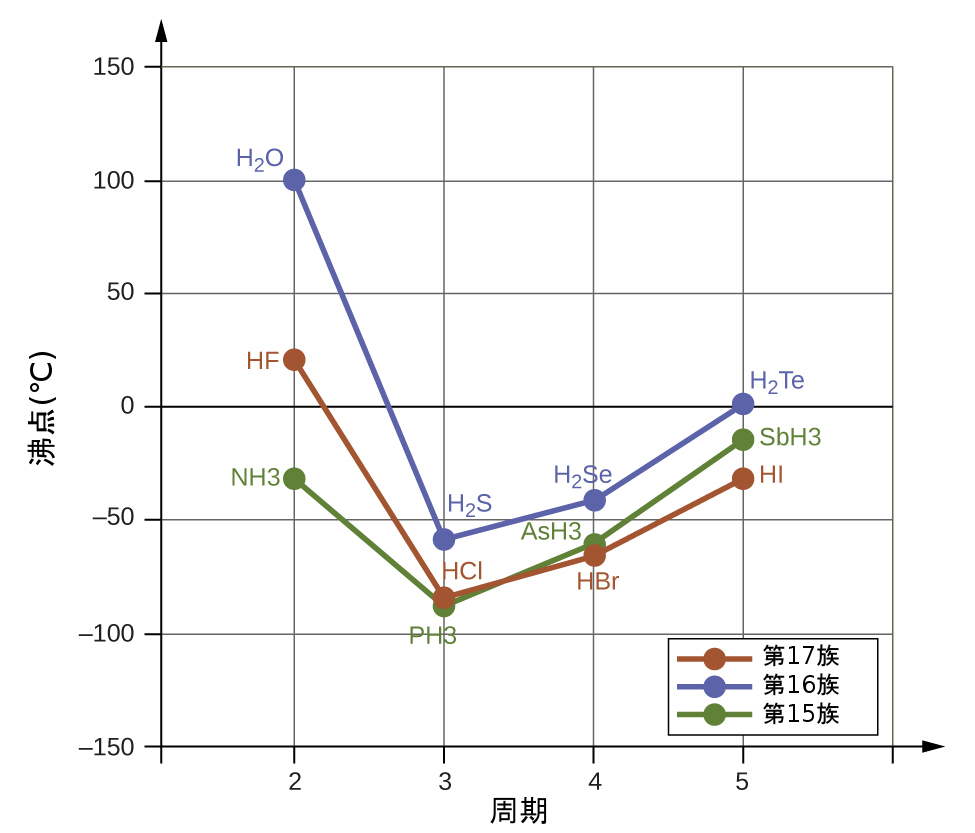
図10.12 | 第3~5周期と比較すると、 第15、16、17族の第2周期の元素(それぞれF、O、N)の二元水素化物は、水素結合による異常に高い沸点を示します。
例題10.3 水素結合の沸点への影響
ジメチルエーテル(CH₃OCH₃)、エタノール(CH₃CH₂OH)、プロパン(CH₃CH₂CH₃)の化合物を考えてみましょう。これらの化合物の沸点は、-42.1°C、-24.8°C、78.4°Cですが、必ずしも順番どおりではありません。それぞれの化合物と、その沸点を組み合わせてください。あなたの推論を説明してください。
解法
VSEPRで予測されるCH₃OCH₃、CH₃CH₂OH、CH₃CH₂CH₃の形状は似ており、またそれらのモル質量(それぞれ46g/mol、46g/mol、44g/mol)も似ています。そのため、それらの化合物は、同じような分散力を示すことになります。CH₃CH₂CH₃は非極性であるため、分散力のみを示すでしょう。CH₃OCH₃は極性であるため、双極子-双極子引力もかかるでしょう。最後に、CH₃CH₂OHは-OH基を持っているので、水素結合として知られている独特に強い双極子-双極子引力がかかることになります。したがって、IMFの強さ、つまり沸点の順番は、CH₃CH₂CH₃ < CH₃OCH₃ < CH₃CH₂OHとなります。プロパンの沸点は-42.1°C、ジメチルエーテルの沸点は-24.8°C、エタノールの沸点は78.5°Cです。
学習内容の確認
エタン(CH₃CH₃)の融点は-183 °C、沸点は-89 °Cです。メチルアミン(CH₃NH₂)の融点と沸点を予測してください。あなたの推論を説明してください。
解答:メチルアミンの融点と沸点はエタンの融点と沸点よりも顕著に高いと予測されます。CH₃CH₃とCH₃NH₂は大きさも質量も似ていますが、メチルアミンは-NH基を持っているため、水素結合を示すでしょう。これはIMFを大きく増加させ、したがって融点や沸点を大きく上昇させます。値を予測することは困難ですが、既知の値は融点-93 °C、沸点-6 °Cです。
さまざまな科学のつながり
水素結合とDNA
デオキシリボ核酸(DNA)はすべての生物に存在するとともに、その生物の特徴を決定する遺伝情報を含んでおり、生命に必要なタンパク質を作るための青写真を提供し、その情報を子孫に伝えるためのテンプレートとしての役割を果たしています。DNA分子は、図10.13に示されるように、2本の(逆)平行な繰り返されるヌクレオチドの鎖で構成されており、よく知られた二重らせん構造を形成しています。
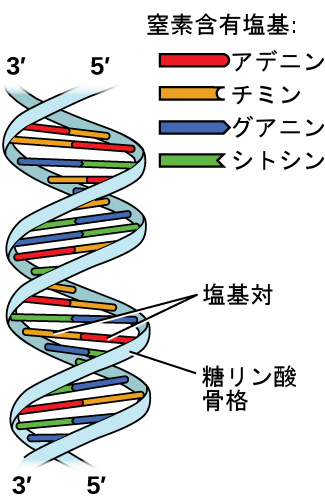
図10.13 | 2つの別々のDNA分子が水素結合を介して一緒に保持されて2本のストランドのらせん構造を形成しています。(credit: modification of work by Jerome Walker, Dennis Myts)
それぞれのヌクレオチドは、片方の側にリン酸基に結合した糖(デオキシリボース)を、もう片方の側に4つの窒素含有塩基のうちの1つを含んでいます。塩基のうち2つ、シトシン(C)とチミン(T)はピリミジンとして知られている単環構造をしています。残りの2つの塩基、アデニン(A)とグアニン(G)は、プリンと呼ばれる二重環構造をしています。これらの塩基は、1つのプリンと1つのピリミジンからなる相補的な塩基対を形成します(アデニンはチミンと対をなし、シトシンはグアニンと対をなします)。それぞれの塩基対は、水素結合によって一緒に保持されます。AとTは2つの水素結合を共有し、CとGは3つの水素結合を共有しています。図10.14に示されるように、どちらの対も似たような形状と構造をしています。
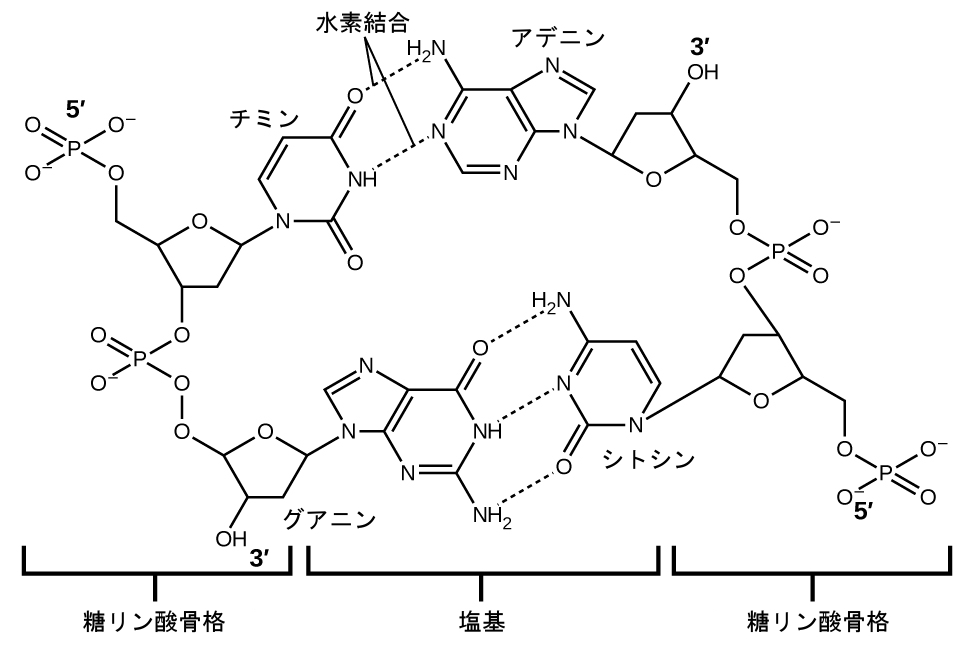
図10.14 | 塩基分子の幾何構造は、アデニンとチミン(AT)の間、およびグアニンとシトシン(GC)の間で最も大きな水素結合、いわゆる「相補的塩基対」をもたらします。
数百万個の水素結合の累積効果により、DNAの2本のストランドが効果的に結合します。重要なことに、DNAの2本のストランドは、比較的簡単に真ん中から「ほどく」ことができます。なぜなら、水素結合は、個々のDNA分子の原子を結合させる共有結合に比べて、比較的弱いからです。これにより、2本のストランドは複製のテンプレートとして機能することができます。
10.2 液体の性質
この節が終わるまでに、あなたは次のことができるようになります:
•接着力と凝集力を区別する
•粘度、表面張力、毛管上昇を定義する
•これらの性質/現象のそれぞれにおける分子間引力の役割を記述する
あなたがコップに水を注いだり、車にガソリンを入れたりするときには、水やガソリンが自由に流れるところを観察できます。しかし、パンケーキにシロップをかけたり、車のエンジンにオイルを追加したりするときには、シロップやモーターオイルは、同じように簡単には流れないことに気づきます。液体の粘度とは、液体の流れにくさの尺度です。水、ガソリン、他の液体など自由に流れる液体は粘度が低いです。図10.15に示されるようなハチミツやシロップ、モーターオイル、他の液体などのように自由に流れない液体は粘度が高いです。私たちは、液体の中を金属のボールが落ちる速度を測ることによって(粘度の高い液体ほどボールの落ちる速度が遅いです)、あるいは、細い管の中を液体が流れる速度を測ることによって(粘度の高い液体ほど流れる速度が遅いです)、粘度を測定することができます。

図10.15 | (a)ハチミツと(b)モーターオイルは粘度の高い液体の例で、ゆっくりと流れます。(credit a: modification of work by Scott Bauer; credit b: modification of work by David Nagy)
液体の流れやすさは、液体の分子間のIMF、分子の大きさと形状、温度によって決まります。表10.2が示すように、液体中の分子の構造がより複雑であればあるほど、また、分子間のIMFが強ければ強いほど、分子がお互いに対して移動することが困難になり、液体の粘度が高くなります。温度が高くなるにつれ、分子の動きが速くなり、その運動エネルギーによって分子をまとめて保持するような力を克服するのが容易になります。したがって、液体の粘度が低下します。
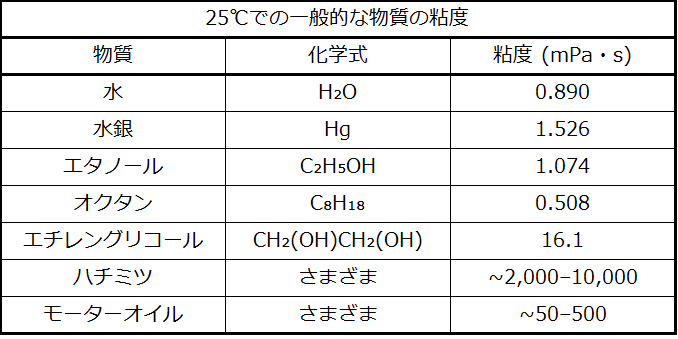
表10.2
ある物質の同一の分子間のさまざまなIMFが、凝集力の例です。液体の中の分子は他の分子に囲まれていて、液体の中の凝集力によって全方向に等しく引き寄せられています。しかしながら、液体の表面にある分子は、約2分の1の分子にしか引き寄せられていません。このように表面にある分子にかかる引力が不均衡であるため、液体は収縮して表面の分子の数が最小になるような形、つまり表面積が最小になるような形になります。小さな液滴は図10.16に示されるように球形になる傾向がありますが、これは球形では体積に対する表面積の比率が最小になるからです。大きな液滴は重力や空気抵抗、表面の相互作用などによる影響を大きく受け、その結果、球形になりにくくなります。

図10.16 | 引力のために、表面積を最小にするような球状の水滴となります。凝集力は球体をまとまったまま保持し、接着力は液滴をクモの巣にくっつけます。(credit photo: modification of work by “OliBac”/Flickr)
表面張力は、液体の表面積を増加させるために必要なエネルギー、または液体表面の長さを所定の量だけ増加させるために必要な力として定義されています。この性質は液体の表面での分子間の凝集力に起因しており、これにより液体の表面がゴム膜を張ったような振る舞いをします。いくつかの液体の表面張力が表10.3に与えられています。一般的な液体の中では、水は分子間の水素結合が強いため、際立って高い表面張力を示します。この高い表面張力の結果として、水の表面は、崩れることなくかなりの力に耐えることができる比較的「強い表面」となります。慎重に水の上に置いたスチールの針は浮きます。図10.17に示されるもののように、いくつかの昆虫は、水よりも密度が高くても、表面張力に支えられることによって水面を移動することができます。
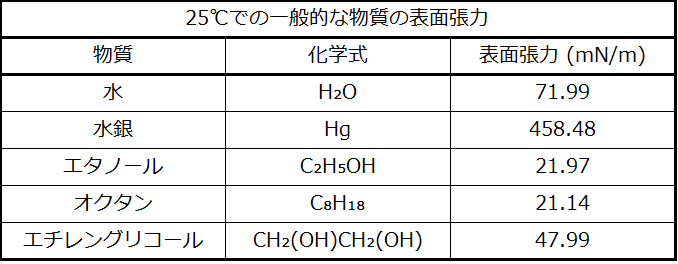
表10.3

図10.17 | 表面張力(右側)は、この昆虫「アメンボ」が水中に沈むのを防いでいます。
2つの異なる分子間の引力であるようなIMFは、接着力と呼ばれます。水が何かの表面に接触するときに何が起こるかを考えてみましょう。もし水の分子と表面の分子との間の接着力が、水の分子間の凝集力に比べて弱い場合、水は表面を「濡らす」ことはありません。たとえば、ワックスを塗った表面やポリエチレンなどの多くのプラスチックを水が濡らすことはありません。水はこれらの表面で水滴を形成します。なぜなら、水滴の中の凝集力が、水とプラスチックの間の接着力よりも大きいからです。水がガラスの上に広がるのは、水とガラスの間の接着力が水の中の凝集力よりも大きいからです。ガラス管の中に水を入れると、水がガラスを濡らして管の側面を這い上がるため、その凹面(表面)はへこんだ形になります。一方、水銀原子間の凝集力は、水銀とガラスとの接着力よりもはるかに大きいです。そのため、水銀はガラスを濡らすことはなく、管の中に入れられたときには突き出た形の凹面を形成します。なぜなら、水銀内の凝集力が水銀を液滴のように引き寄せる傾向があるからです(図10.18)。

図10.18 | 凝集力と接着力の相対的な強さの違いにより、ガラス管内の水銀(左側)と水(右側)では凹面の形状が異なります。(credit: Mark Ott)
図10.19に示されるように、こぼれたワインの中にペーパータオルの一端を入れると、液体がペーパータオルに吸い取られます。シャワーを浴びた後に体を乾かすために布のタオルを使うときにも、同じようなプロセスが起こります。これらは毛管現象の例です。毛管現象とは、液体が多孔質材料の表面や他の液体分子に引き寄せられて、多孔質材料の中を流れるときの現象です。液体と多孔質材料との間の接着力は、液体内の凝集力と組み合わさって、重力に逆らって液体を上方に移動させるのに十分なほど強くなることがあります。
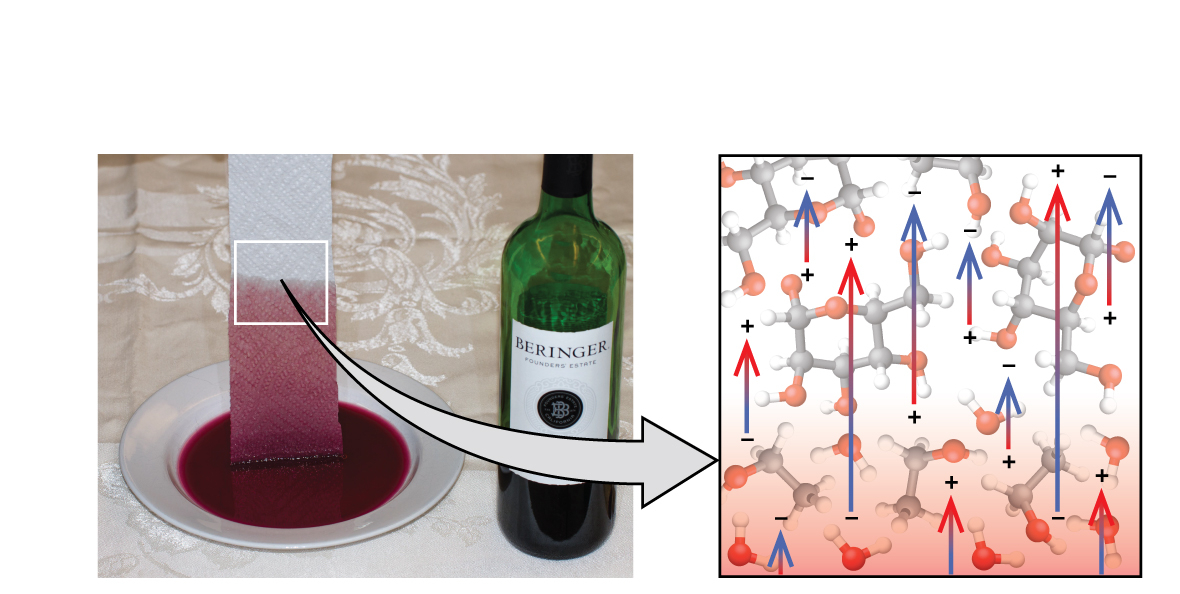
図10.19 | ワインはペーパータオルに吸い取られます(左側)。これは、ペーパータオルのセルロース繊維の-OH基に対する水(およびエタノール)分子の強い引力と、他の水(およびエタノール)分子に対する水分子の強い引力によるものです(右側)。(credit photo: modification of work by Mark Blaser)
タオルが水のような液体を吸い上げるのは、タオルの繊維が水分子と引き合う分子でできているからです。ほとんどの布製のタオルは綿でできており、ペーパータオルは一般的に紙パルプでできています。どちらも-OH基を多く含むセルロースの長い分子で構成されています。水分子はこれらの-OH基に引き寄せられて、それらの-OH基と水素結合を形成します。これがH₂O分子をセルロース分子の上に引き寄せます。また、水分子はお互い同士も引き合うので、大量の水がセルロース繊維に引き寄せられます。
図10.20に示されるように、小径管の一端を液体に浸したときにも、毛管現象が起こります。液体の分子が管の分子に強く引きつけられると、液体の重さと接着力が均衡するまで液体が管の内部を這い上がります。管の直径が小さくなればなるほど、液体が上昇する高さは高くなります。水や溶解した栄養分が土壌から根を通って植物に運ばれるのは、部分的には木部と呼ばれる植物の細胞で発生する毛管現象によっています。毛管現象は、少量の混合物を分離するために一般的に使用されている実験室の技術である薄層クロマトグラフィーの基礎となっています。あなたは目を潤滑に保つために涙を常に供給し、涙液を送り出すために毛管現象に頼っています。
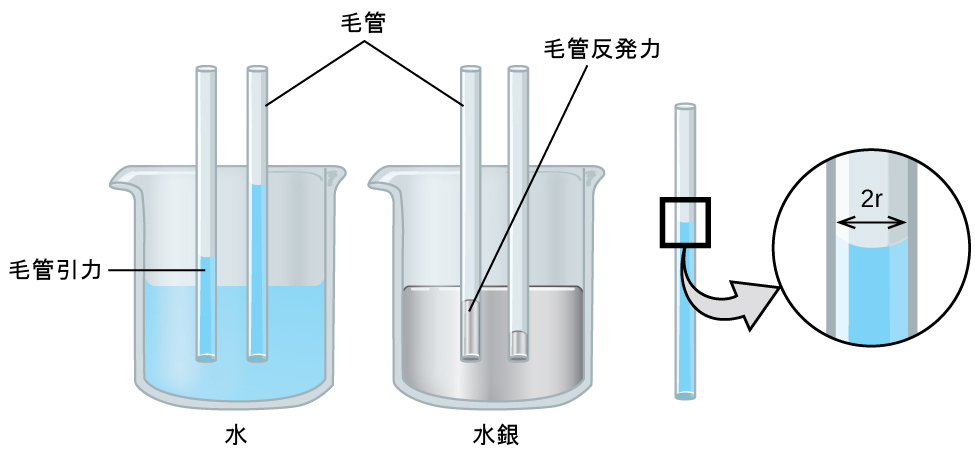
図10.20 | 接着力と凝集力の相対的な強さに応じて、液体はガラス管内を上昇 (水など) したり、下降 (水銀など) したりします。上昇(または下降)の程度は液体の表面張力に正比例し、液体の密度と管の半径に反比例します。
毛管内で液体が上昇する高さは、以下の式に示されるように、いくつかの要因によって決まります:
\[ h =\frac{2T cosθ}{rρg} \]
この式において、hは毛管の外側の液体の表面に対する管内の液体の高さ、Tは液体の表面張力、θは液体と管の接触角、rは管の半径、ρは液体の密度、gは重力による加速度9.8 m/s²です。管が液体分子を強く引き寄せる材料で作られている場合、液体分子は表面に完全に広がり、接触角は0°に相当します。これがガラス管の中を水が上昇する場合の状況です。
例題10.4 毛管上昇
25 °Cの場合、内径 0.25 mm のガラス管の中で水はどれだけの高さまで上昇するでしょうか?水は、T = 71.99 mN/m、ρ = 1.0 g/cm³です。
解法
液体は以下の式によって与えられる高さhまで上昇します:
\[ h =\frac{2T cosθ}{rρg} \]
ニュートンはkg m/s²と定義されていますので、与えられた表面張力は 0.07199 kg/s²に相当します。与えられた密度は、適切に打ち消される単位に変換しなければなりません:ρ = 1000 kg/m³。管の直径はメートルでは0.00025 mであるため、半径は0.000125 mとなります。水に浸したガラス管の場合、接触角はθ = 0°なので cosθ = 1となります。最後に、地球上の重力による加速度はg = 9.8 m/s²です。これらの値を式に代入し、単位を打ち消すと、以下のようになります:
\[ h =\rm \frac{2(0.07199\ kg/s^2)}{(0.000125\ m)(1000\ kg/m^3)(9.8\ m/s^2)}= 0.12\ m = 12\ cm \]
学習内容の確認
あるガラス管の中で水が8.4cmの高さまで上昇しました。この細管の直径は何ですか?
解答:直径 = 0.36 mm
日常生活の中の化学
毛管現象の生物医学的応用
多くの医療検査では(たとえば、糖尿病患者のグルコースの量やスポーツ選手のヘマトクリット値を測定するために)、少量の血液を採取する必要があります。この方法は、図10.21に示されるように、毛管現象、つまり液体が重力に逆らって小さな管を上に流れる能力を利用して簡単に行うことができます。指を刺すと、血液の滴が形成され、表面張力(滴の表面での分子間の不均衡な引力)のためにまとまって保持されます。次に、細い径のガラス管の開放端が血液の滴に触れると、血液中の分子とガラス表面の分子との間の接着力により、血液が管の上部へと引き上げられます。血液が管の上に向かってどのくらいの距離を進むかは、管の直径(および流体の種類)によって異なります。小さな管は、所与の体積の血液に対して比較的大きな表面積を持っており、その結果、より大きな(相対的に)引力が発生し、血液をより管の上まで引き上げることができます。液体自体は、自身の凝集力によってまとまって保持されています。管内の液体の重量が毛管現象に関連した上向きの力に等しい下向きの力を発生させると、液体は上昇を停止します。
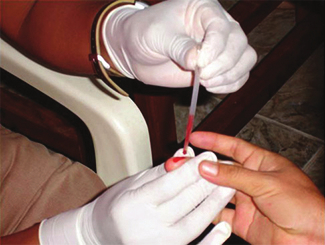
図10.21 | 医学的分析のための採血は、血液を小径のガラス管に引き込む毛管現象によって行われます。(credit: modification of work by Centers for Disease Control and Prevention)
10.3 相転移
この節が終わるまでに、あなたは次のことができるようになります:
•相転移と相転移温度を定義する
•相転移温度と分子間引力の関係を説明する
•典型的な加熱・冷却曲線によって表される過程を記述し、これらの過程に伴う熱流とエンタルピーの変化を計算する
私たちは、物理状態の変化、つまり相転移を多くの方法で目撃し、利用しています。グローバルな重要性を持つ一例として、水の蒸発、凝縮、凍結、融解を考えてみましょう。これらの状態変化は、地球の水循環や、他の多くの自然現象、そして私たちの生活にとって中心的な重要性を持つ技術的なプロセスの本質的な側面です。この節では、相転移の本質的な側面を探ります。
蒸発と凝縮
液体が密閉された容器の中で蒸発したときには、気体分子は逃げられません。この気相分子がランダムに移動している間に凝縮相の表面に衝突することがあり、場合によってはこの衝突によって分子が再び凝縮相に入ります。気相から液体への変化は凝縮と呼ばれます。凝縮の速度が蒸発の速度と等しくなると、容器内の液体の量も蒸気の量も変わることはありません。その時、容器の中の蒸気は液体と平衡にあると言われます。凝縮相と気相の間では分子が絶えず交換されているので、これは静的な状態ではないということを覚えておいてください。これが動的平衡の一例です。動的平衡とは、相互の過程(たとえば蒸発と凝縮)が等しい速度で起こる系の状態のことです。密閉容器内の液体と平衡にある蒸気が所定の温度でかける圧力を、液体の蒸気圧(または平衡蒸気圧)といいます。蒸気と接触する液体の表面の面積や容器の大きさは蒸気圧に影響しませんが、それらは平衡に達するまでに要する時間に影響を与えます。私たちは、図10.22に示されるもののような密閉容器に試料を入れ、マノメーターを使って蒸気が凝縮相と平衡にあることに起因する圧力の上昇を測定することによって、液体の蒸気圧を測定することができます。
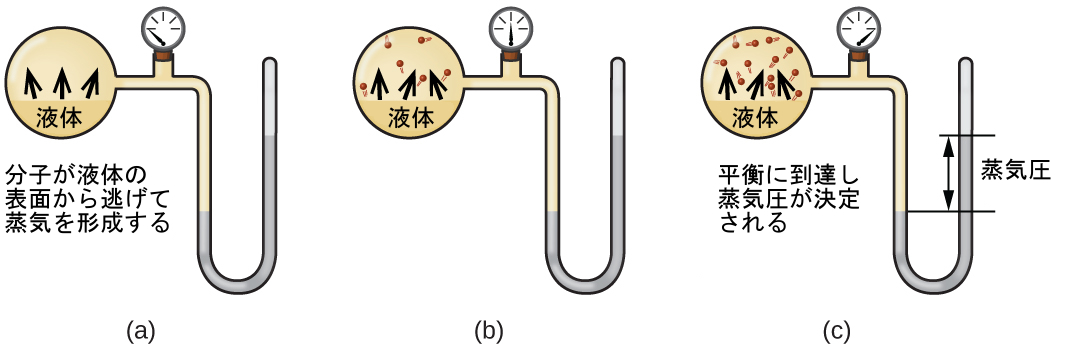
図10.22 | 密閉容器内では、(a)液体から逃げて気体になる分子の速度が、(b)増加し、最終的には(c)液体に入る気体分子の速度と等しくなったときに動的平衡に達します。この平衡に達すると、蒸発と凝縮の過程は続きますが、気体の蒸気圧は一定です。
液体中の分子の化学的同一性が、可能な分子間引力の種類(および強さ)を決定します。その結果、異なる物質は異なる平衡蒸気圧を示すことになります。相対的に強い分子間引力は、蒸発を妨げる役割を持つことに加え、気相分子が液体の表面と衝突したときに気相分子を「再捕獲」するのに役立つため、結果として比較的低い蒸気圧となります。弱い分子間引力では、蒸発への障壁が少なく、また、気体を再捕獲する可能性が低くなるため、比較的高い蒸気圧が得られます。以下の例題では、分子間引力に対する蒸気圧の依存性を例示します。
例題10.5 蒸気圧をIMFの観点から説明する
これら4つの化合物について示される構造式が与えられた場合、それらの相対的な蒸気圧をIMFの種類と程度の観点から説明してください:

解法
ジエチルエーテルは非常に小さな双極子を持ち、分子間引力のほとんどはロンドン力です。この分子は検討している4つの中で最大のものですが、そのIMFは最も弱く、結果として、その分子は最も容易に液体から逃げます。ジエチルエーテルはまた、蒸気圧も最も高いです。エタノールはサイズが小さいため、ジエチルエーテルよりも弱い分散力を示します。しかしながら、エタノールは水素結合が可能であるため、全体的に強いIMFを示します。これは、任意の温度で液体から逃げる分子が少ないことを意味するため、エタノールはジエチルエーテルよりも低い蒸気圧を有します。水は前の2つの物質よりもはるかに小さく、弱い分散力を示します。しかし、水はその大きな水素結合のために、ジエチルエーテルやエタノールよりも分子間引力が強く、液体から逃げる分子が少なく、蒸気圧が低くなります。エチレングリコールは2つの-OH基を持っているので、水と同様に、大きな水素結合を示します。エチレングリコールは水よりもはるかに大きく、したがって、より大きなロンドン力を経験します。エチレングリコールの全体的なIMFは、これらの4つの物質の中で最大であり、それは、エチレングリコールの蒸発速度が最も遅く、その結果、蒸気圧が最も低いことを意味します。
学習内容の確認
20 °Cでのいくつかのアルコールの蒸気圧がこの表に示されています。これらのアルコールの蒸気圧を、これらのアルコールについてのIMFの種類と程度の観点から説明してください:

解答:これらの化合物はすべて水素結合を示します。分子がそれらの強いIMFを克服するのは難しいため、蒸気圧は比較的低くなります。分子の大きさがメタノールからブタノールへと大きくなるにつれ、分散力が大きくなり、観測されているように蒸気圧が低下します:Pメタノール > Pエタノール > Pプロパノール > Pブタノールとなります。
温度が上昇すると、分子の平均KEが増加するために、液体の蒸気圧も上昇します。任意の温度では、物質の分子はある範囲の運動エネルギーを呈しており、所定の割合の分子はIMFを克服して液体から逃げる(蒸発する)のに十分なエネルギーを持っています。温度が高くなると、図10.23に示されるように、より多くの割合の分子が液体から逃げるのに十分なエネルギーを持つことになります。より多くの分子が単位時間あたりに逃げ出すことと、逃げ出す分子の平均速度がより速いことの両方が、蒸気圧の上昇に寄与しています。
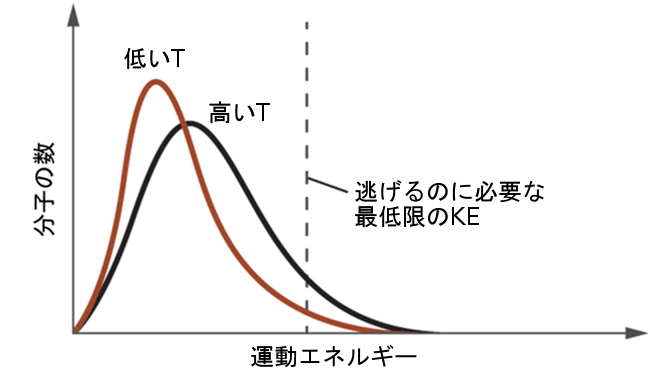
図10.23 | 温度は液体中の分子の運動エネルギーの分布に影響を与えます。温度が高くなると、液体から気相に逃げるのに必要な運動エネルギーKEを持つ分子が多くなります。
沸点
蒸気圧が外部の大気圧と等しくなるほど上昇すると、液体は沸点に達します。液体の沸点とは、その平衡蒸気圧と気体状の周囲環境によって液体に及ぼされる圧力とが等しくなる温度のことです。開放された容器に入っている液体の場合、この圧力は地球の大気によるものです。液体の標準沸点は、周囲環境の圧力が1atm(101.3kPa)であるときの沸点として定義されています。図10.24は、いくつかの異なる物質について、温度による蒸気圧の変化を示しています。沸点の定義を考えると、この曲線は、液体の沸点が周囲環境の圧力に依存していることを描くものとして見ることができます。
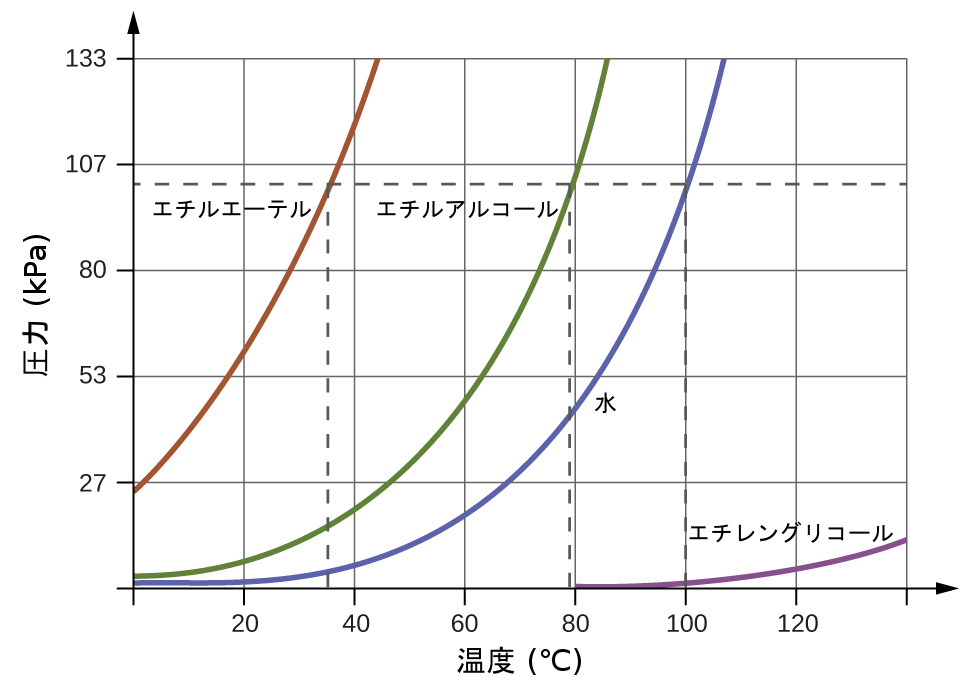
図10.24 | 液体の沸点は、その平衡蒸気圧が周囲の大気の圧力と等しくなる温度です。標準沸点は1atm(101.3kPa)の圧力に対応する沸点です。
例題10.6 減圧下での沸点
コロラド州リードヴィル(標高10,200フィート)の典型的な大気圧は68kPaです。図10.24のグラフを使って、この標高での水の沸点を決定してください。
解法
図10.24の水の蒸気圧と温度のグラフは、約90°Cで水の蒸気圧が68kPaであることを示しています。したがって、約90°Cで、水の蒸気圧はリードヴィルの大気圧と等しくなり、水は沸騰することになるでしょう。
学習内容の確認
エベレスト山の斜面にあるベースキャンプで、エチルエーテルの沸点を測定したところ、10°Cでした。図10.24を使って、このキャンプの大気圧のおおよその値を決定してください。
解答:約40kPa (0.4atm)
ある物質の蒸気圧と温度との間の定量的な関係は、クラウジウス-クラペイロンの式によって記述されます:
\[ P = Ae^{−ΔH_{蒸発} /RT} \]
ここでΔH蒸発は液体の蒸発のエンタルピー、Rは気体定数、Aは物質の化学的同一性に依存する値を持つ定数です。この式では、温度Tはケルビンでなければなりません。この式はしばしば対数形式に再配置され、線形方程式が得られます:
\[ {\rm ln}P = −\frac{ΔH_{蒸発}}{RT}+ {\rm ln} A \]
この線形方程式は、以下の例題で示されるように、さまざまな計算で使用するのに便利な2点形式で表現することができます。もし温度T₁で蒸気圧がP₁であり、温度T₂で蒸気圧がP₂であるとすると、対応する線形方程式は以下のようになります:
\[ {\rm ln}P_1 = −\frac{ΔH_{蒸発}}{RT_1}+ {\rm ln} A \hspace{10pt}および\hspace{10pt}{\rm ln}P_2 = −\frac{ΔH_{蒸発}}{RT_2}+ {\rm ln} A \]
定数Aは同じなので、これら2つの式を並べ替えてln Aを独立させ、それらを互いに等号で結ぶことができます:
\[ {\rm ln}P_1 +\frac{ΔH_{蒸発}}{RT_1}= {\rm ln}P_2 +\frac{ΔH_{蒸発}}{RT_2} \]
これを組み合わせると、以下のようになります:
\[ {\rm ln}\left(\frac{P_2}{P_1}\right)=\frac{ΔH_{蒸発}}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right) \]
例題10.7 蒸発のエンタルピーを推定する
イソオクタン(2,2,4-トリメチルペンタン)は、オクタン価が100です。イソオクタンは、ガソリンのオクタン価システムの基準の1つとして使用されています。34.0°Cでのイソオクタンの蒸気圧は10.0kPa、98.8°Cでの蒸気圧は100.0kPaです。この情報を用いて、イソオクタンの蒸発のエンタルピーを推定してください。
解法
蒸発のエンタルピーΔH蒸発は、クラウジウス-クラペイロンの式を使うことによって決定することができます:
\[ {\rm ln}\left(\frac{P_2}{P_1}\right)=\frac{ΔH_{蒸発}}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right) \]
2つの蒸気圧-温度値(T₁ = 34.0 °C = 307.2 K、P₁ = 10.0 kPaとT₂ = 98.8 °C = 372.0 K、P₂ = 100 kPa)があるので、これらをこの式に代入してΔH蒸発について解くことができます。クラウジウス-クラペイロンの式を並べ替えて、ΔH蒸発について解くと、以下のようになります:
\[ ΔH_{蒸発} =\frac{R⋅{\rm ln}\left(\frac{P_2}{P_1}\right)}{\left(\frac{1}{T_1}−\frac{1}{T_2}\right)} =\rm \frac{(8.3145\ J/mol⋅K)⋅{\rm ln}\left(\frac{100\ kPa}{10.0\ kPa}\right)}{\left(\frac{1}{307.2\ K}−\frac{1}{372.0\ K}\right)} = 33,800\ J/mol = 33.8\ kJ/mol \]
両方のPの値で一致している限り圧力はどの単位でも使うことができますが、クラウジウス-クラペイロンの式が妥当であるためには、温度はケルビンでなければならないということに注意してください。
学習内容の確認
20.0°Cでのエタノールの蒸気圧は5.95kPa、63.5°Cでの蒸気圧は53.3kPaです。この情報を用いて、エタノールの蒸発のエンタルピーを推定してください。
解答:41,360 J/molまたは41.4 kJ/mol
例題10.8 温度(または蒸気圧)を推定する
ベンゼン(C₆H₆)の場合、標準沸点は80.1°C、蒸発のエンタルピーは30.8 kJ/molです。大気圧が83.4kPaであるコロラド州デンバーでのベンゼンの沸点は何ですか?
解法
もしある点での温度・蒸気圧と、蒸発のエンタルピーΔH蒸発がわかっているならば、異なる蒸気圧に対応する温度(または異なる温度に対応する蒸気圧)は、クラウジウス-クラペイロンの式を用いて決定することができます:
\[ {\rm ln}\left(\frac{P_2}{P_1}\right)=\frac{ΔH_{蒸発}}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right) \]
標準沸点とは蒸気圧が海面での大気圧と等しくなる温度であるので、私たちは1つの蒸気圧-温度の値(T₁ = 80.1 °C = 353.3 K、P₁ = 101.3 kPa、ΔH蒸発 = 30.8 kJ/mol)がわかっています。また、私たちは蒸気圧P₂ = 83.4 kPaに対応する温度(T₂)を求めようとしています。これらの値をクラウジウス-クラペイロンの式に代入して、T₂を求めることができます。クラウジウス-クラペイロンの式を並べ替えてT₂について解くと、以下のようになります:
\[ \begin{array}{ll} T_2=\left\lgroup\frac{−R⋅{\rm ln}\left(\frac{P_2}{P_1}\right)}{ΔH_{蒸発}}+\frac{1}{T_1}\right\rgroup^{−1}\\ =\rm \left\lgroup\frac{−(8.3145\ J/mol⋅K)⋅{\rm ln}\left(\frac{83.4\ kPa}{101.3\ kPa}\right)}{30,800\ J/mol}+\frac{1}{353.3\ K}\right\rgroup^{−1}\\ =\rm 346.9\ K\ または\ 73.8\ °C \end{array} \]
学習内容の確認
アセトン(CH₃)₂COの場合、標準沸点は56.5°C、蒸発のエンタルピーは31.3 kJ/molです。25.0°Cでのアセトンの蒸気圧は何ですか?
解答:30.1 kPa
蒸発のエンタルピー
蒸発は吸熱過程です。この冷却効果は、あなたがプールやシャワーから出るときに明白に現れます。あなたの肌の上の水が蒸発するときには、その水が肌から熱を奪い、あなたに寒さを感じさせます。蒸発過程に伴うエネルギーの変化が、蒸発のエンタルピーΔH蒸発です。たとえば、標準温度での水の蒸発は以下のように表されます:
\[ {\rm H_2O\ (l) ⟶ H_2O\ (g)} \hspace{20pt} ΔH_{蒸発} = {\rm 44.01\ kJ/mol} \]
熱化学の章で説明したように、吸熱過程の逆は発熱過程です。そのため、気体の凝縮は熱を放出します:
\[ {\rm H_2O\ (g) ⟶ H_2O\ (l)} \hspace{20pt} ΔH_{凝縮} = −ΔH_{蒸発} = {\rm −44.01\ kJ/mol} \]
例題10.9 蒸発のエンタルピーを使用する
私たちの体を冷やす方法の1つは、汗に含まれる水分の蒸発です(図10.25)。非常に暑い気候では、私たちは1日に1.5Lもの汗をかくことがあります。汗は純粋な水ではありませんが、水であると仮定することで蒸発によって取り除かれる熱量のおおよその値が得られます。T=37°C(通常の体温)で1.5Lの水(1.5kg)を蒸発させるのに必要な熱量はどれだけですか?37°Cでは、ΔH蒸発=43.46kJ/molです。

図10.25 | 汗の蒸発は体を冷やすのに役立ちます。(credit: “Kullez”/Flickr)
解法
私たちは、既知の汗の量(ただの水と近似します)から始め、与えられた情報を使用して必要な熱量に変換します:
\[ \rm 1.5\ L ×\frac{1000\ g}{1\ L}×\frac{1\ mol}{18\ g}×\frac{43.46\ kJ}{1\ mol}= 3.6 × 10^3\ kJ \]
したがって、1.5Lの水を蒸発させることによって3600kJの熱が取り除かれます。
学習内容の確認
液体アンモニア(NH₃)100.0gをその沸点で蒸発させるのに必要な熱量は、蒸発のエンタルピーが4.8kJ/molの場合では、どれだけですか?
解答:28 kJ
融解と凍結
私たちが結晶性固体を加熱すると、その原子、分子、またはイオンの平均エネルギーが増加し、固体が高温になります。ある時点で、加えられたエネルギーは、固体の分子またはイオンを固定された位置に保持する力を部分的に克服するのに十分な大きさになり、固体は液体状態に移行する過程、すなわち融解を始めます。この時点で、固体の温度は、継続的な熱の投入にもかかわらず上昇を停止し、固体のすべてが融解するまで一定のままに留まります。固体がすべて溶けた後になってようやく、加熱を続けることで液体の温度が上昇します(図10.26)。

図10.26 | (a)このビーカーの氷の温度は-12.0 °Cです。(b)10分後、氷は空気中の熱を十分に吸収して0°Cまで温まっています。少量が融けています。(c)30分後、氷はさらに多くの熱を吸収しましたが、その温度はまだ0°Cのままです。氷は温度を変えることなく融けます。(d)すべての氷が溶けた後になってようやく、吸収した熱で温度が22.2°Cまで上昇します。(credit: modification of work by Mark Ott)
もし私たちが融解中に加熱を止めて、固体と液体の混合物を完全に断熱された容器に入れて熱が出入りしないようにすると、固相と液相は平衡状態を保ったままになります。これは、非常に優れた魔法瓶の中の氷と水の混合物の状況とほぼ同じで、熱はほとんど出入りせず、固体の氷と液体の水の混合物は何時間もそのまま残っています。平衡にある固体と液体の混合物では、融解と凍結の相互変換的な過程が等速で起こり、固体と液体の量は一定に保たれます。ある物質の固相と液相が平衡にあるような温度は、固体の融点または液体の凝固点と呼ばれます。通常、考慮している相転移の方向によってどちらか一方の用語を使用します(たとえば、固体から液体への相転移(融点)や液体から固体への相転移(凝固点))。
結晶性固体の融解のエンタルピーと融点は、結晶中に存在する単位間の引力の強さに依存します。弱い引力を持つ分子は、融点の低い結晶を形成します。より強い引力を持つ粒子からなる結晶は、より高い温度で融解します。
ある物質の1モルが固体状態から液体状態に変化するのに必要な熱量が、その物質の融解のエンタルピーΔH融解です。氷の融解のエンタルピーは0°Cで6.0kJ/molです。融解は吸熱過程です:
\[ {\rm H_2O\ (s) ⟶ H_2O\ (l)} \hspace{20pt} ΔH_{融解} = {\rm 6.01\ kJ/mol} \]
逆の過程である凍結は、0°Cでのエンタルピー変化が-6.0kJ/molの発熱過程です:
\[ {\rm H_2O\ (l) ⟶ H_2O\ (s)} \hspace{20pt} ΔH_{凍結} = -ΔH_{融解} = {\rm -6.01\ kJ/mol} \]
昇華と凝結
固体の中には、昇華として知られる過程を経て、液体状態を迂回して気体状態に直接転移するものもあります。室温と標準圧力では、ドライアイス(固体CO₂)の小片は昇華し、液体を形成することなく徐々に消えていくように見えます。雪や氷は水の融点以下の温度で昇華します。これはゆっくりとしたプロセスですが、風や高地での気圧の低下によって加速されることがあります。固体のヨウ素を温めると、固体が昇華し、鮮やかな紫色の蒸気が発生します(図10.27)。昇華の逆の現象を凝結といい、気体状の物質が液体を介さずに直接固体に凝縮する現象です。霜の形成は凝結の一例です。

図10.27 | 管の底部で固体ヨウ素を昇華させると紫色の気体が発生し、それが管の上部の冷たい部分に固体ヨウ素として凝結します。(credit: modification of work by Mark Ott)
蒸発と同様に、昇華の過程では、分子間の引力を克服するためにエネルギーを投入する必要があります。昇華のエンタルピーΔH昇華は、ある物質の1モルを固体状態から気体状態に変換するのに必要なエネルギーです。たとえば、二酸化炭素の昇華は以下のように表されます:
\[ {\rm CO_2\ (s) ⟶ CO_2\ (g)} \hspace{20pt} ΔH_{昇華} = {\rm 26.1\ kJ/mol} \]
同様に、逆の過程である凝結についてのエンタルピー変化は、昇華の場合と同じ大きさですが、符号は逆です:
\[ {\rm CO_2\ (g) ⟶ CO_2\ (s)} \hspace{20pt} ΔH_{凝結} = -ΔH_{昇華} = {\rm -26.1\ kJ/mol} \]
所定の相転移を達成するために克服しなければならない分子間の引力の程度を考えてみましょう。固体から液体への変換は、それらの引力を部分的にのみ克服する必要があります。気体状態への転移は、それらの引力を完全に克服する必要があります。その結果、物質の融解のエンタルピーは蒸発のエンタルピーよりも小さくなります。この同じ論理を用いて、ある物質のすべての相変化のエンタルピー間の近似的な関係を導き出すことができます。完全に正確な記述というわけではありませんが、昇華は、ヘスの法則を適用するために、融解の後に蒸発するという連続した2段階のプロセスとして簡便な形でモデル化することができます。このように見ると、物質の昇華のエンタルピーは、図10.28に示されているように、融解と蒸発のエンタルピーの合計として推定することができます。たとえば、以下のようになります:
\[ \begin{array}{ll} 固体 ⟶ 液体 \hspace{20pt} ΔH_{融解}\\ 液体 ⟶ 気体 \hspace{20pt} ΔH_{蒸発}\\ \hline 固体 ⟶ 気体 \hspace{20pt} ΔH_{昇華} = ΔH_{融解} + ΔH_{蒸発} \end{array} \]
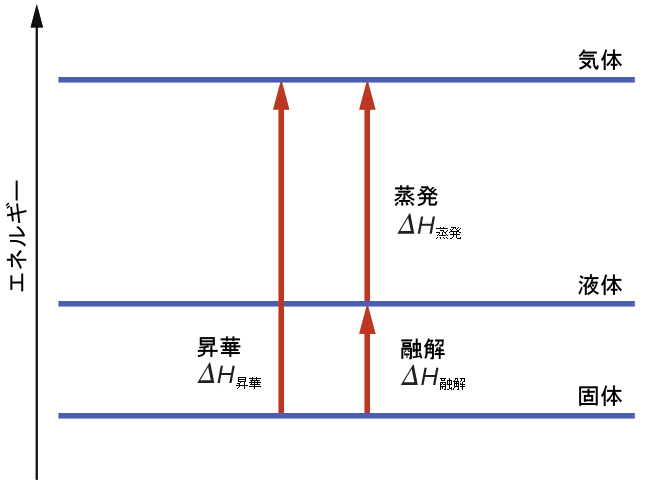
図10.28 | ある物質について、融解のエンタルピーと蒸発のエンタルピーの和は昇華のエンタルピーとほぼ等しくなります。
加熱・冷却曲線
熱化学の章では、物質が吸収または放出する熱量qとそれに伴う温度変化ΔTの関係を導入しました:
\[ q = mcΔT \]
ここで、mは物質の質量であり、cはその比熱です。この関係は、加熱または冷却されているものの、状態変化を起こしていない物質に対して適用されます。加熱または冷却されている物質がその相転移に対応する温度に達すると、熱のさらなる獲得または損失は、分子の運動エネルギーの増減ではなく、分子間引力の減少または増強という結果につながります。物質が状態変化を起こしている間は、その温度は一定のままです。図10.29は、典型的な加熱曲線を示しています。
水の入った鍋を沸騰するまで加熱する例を考えてみましょう。コンロのバーナーはほぼ一定の割合で熱を供給し、最初はこの熱が水の温度を上昇させます。水が沸点に達すると、コンロのバーナーからの熱が継続的に供給されているにもかかわらず温度は一定に保たれます。水が沸騰している間は、この温度が維持されます。バーナーの設定を上げて供給する熱量を増やしたとしても、水温は上昇しませんが、その代わりに沸騰が激しく(急激に)なります。この振る舞いは他の相転移でも観察されます:たとえば、状態変化が進行している間は、温度は一定に保たれています。
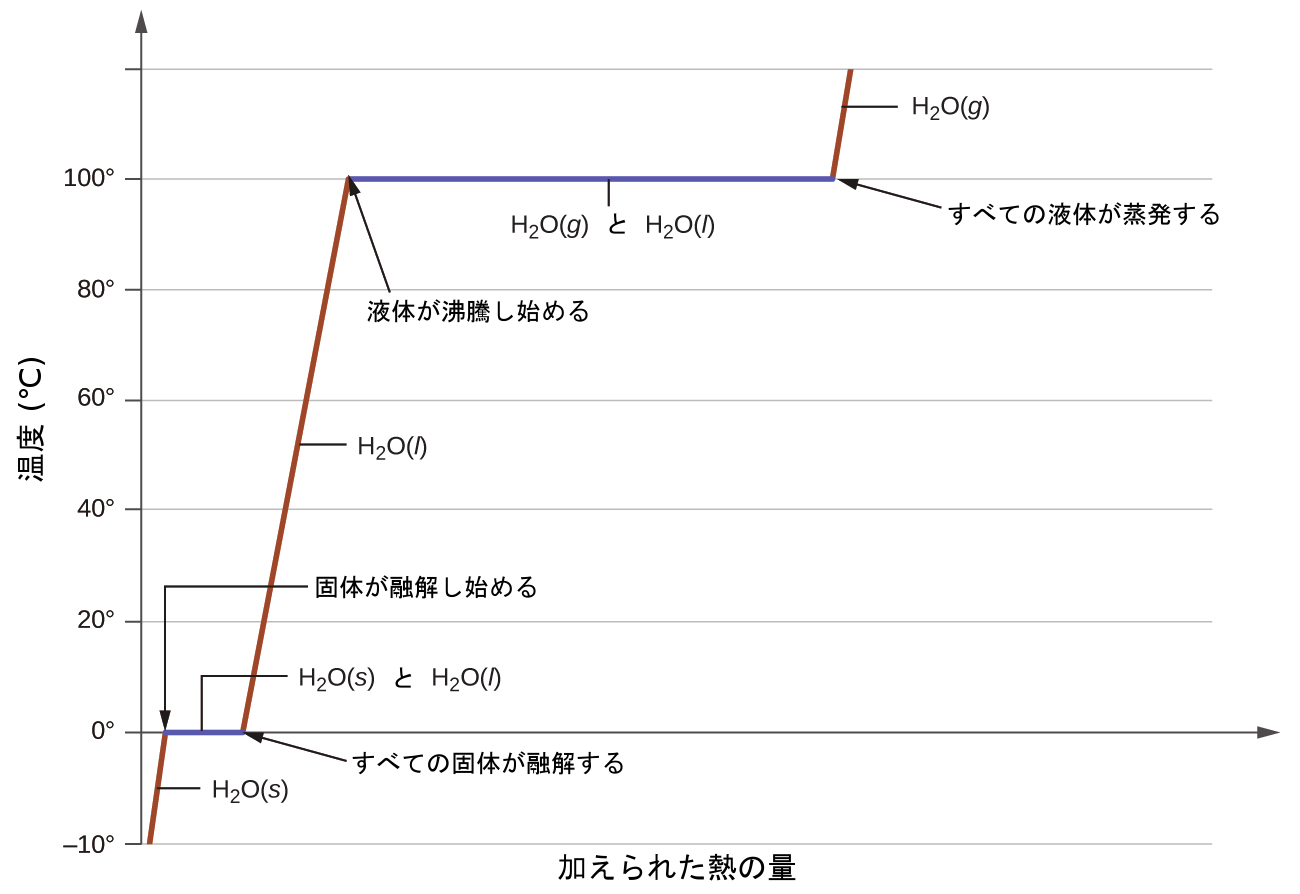
図10.29 | ある物質についての典型的な加熱曲線は、物質が吸収する熱の量が増えるにつれて温度が変化していく様子を表しています。曲線の水平部分(温度が一定の領域)は、物質が相転移しているときに現れます。
例題10.10 物質の温度変化と相変化に必要な熱の総量
-15°Cである135gの氷を、120°Cの水蒸気に変えるためにはどれだけの熱が必要ですか?
解法
記述されている転移は、以下のステップを含みます:
1.氷を-15°Cから0°Cまで加熱する
2.氷を融解する
3.水を0°Cから100°Cまで加熱する
4.水を沸騰させる
5.水蒸気を100°Cから120°Cまで加熱する
ある物質の温度を変化させるのに必要な熱(相変化のない状態で)は、q = m × c × ΔTです(以前の熱化学の章を参照)。相変化を引き起こすのに必要な熱は、q = n × ΔHで与えられます。
これらの式とともに、氷、水、水蒸気の比熱、融解と蒸発のエンタルピーについての適当な値を用いると、以下のようになります:
\[ \begin{array}{ll} q_{\rm total} = (m⋅c⋅ΔT)_{氷} + n⋅ΔH_{融解} + (m⋅c⋅ΔT)_{水} + n⋅ΔH_{蒸発} + (m⋅c⋅ΔT)_{蒸気}\\ \rm =(135\ g⋅2.09\ J/g⋅°C⋅15°C) +\left(135\ g⋅\frac{1\ mol}{18.02\ g} ⋅6.01\ kJ/mol\right)\\ \rm \hspace{8pt} +(135\ g⋅4.18\ J/g⋅°C⋅100°C) +\left(135\ g⋅\frac{1\ mol}{18.02\ g} ⋅40.67\ kJ/mol\right)\\ \rm \hspace{8pt} +(135\ g⋅1.84\ J/g⋅°C⋅20°C)\\ \rm = 4230\ J + 45.0\ kJ + 56,500\ J + 305\ kJ + 4970\ J \end{array} \]
J単位の量をkJ単位に変換すると、それらの量を合計することができ、必要な熱の総量が得られます:
\[ \rm = 4.23\ kJ + 45.0\ kJ + 56.5\ kJ + 305\ kJ + 4.97\ kJ = 416\ kJ \]
学習内容の確認
80.0°Cである94.0gの水を冷却して、-30.0°Cの氷を生成するときに放出される熱の総量は何ですか?
解答:68.7 kJ
10.4 相図
この節が終わるまでに、あなたは次のことができるようになります:
•典型的な相図の構成と使用方法を説明する
•相図を使用して、与えられた温度と圧力での安定した相を特定し、それらの性質の変化に起因する相転移を記述する
•物質の超臨界流体相を記述する
前節では、温度による液体の平衡蒸気圧の変化について説明しました。沸点の定義を考慮すると、蒸気圧と温度の描画は、圧力によって液体の沸点がどのように変化するかを表します。また、物質の融点(または凝固点)を決定するための加熱・冷却曲線の使用についても説明しました。このような測定を広い範囲の圧力で行うと、相図として図的に表示することができるデータが得られます。相図は、ある物質の液体-気体、固体-液体、固体-気体の相転移平衡についての圧力と温度の描画を組み合わせたものです。これらの図は、圧力と温度の特定の条件下で存在する物理状態を示すものであり、また、相転移温度(融点、昇華点、沸点)の圧力依存性を与えるものです。純物質についての典型的な相図が図10.30に示されています。
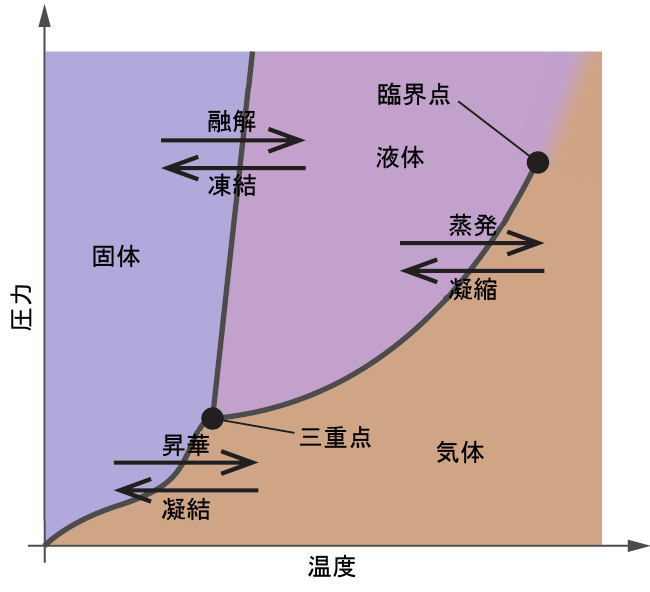
図10.30 | 物質の物理的状態と相転移温度が、相図の中で図的に表現されています。
これらの描画の有用性を説明するために、図10.31に示される水の相図について検討してみましょう。
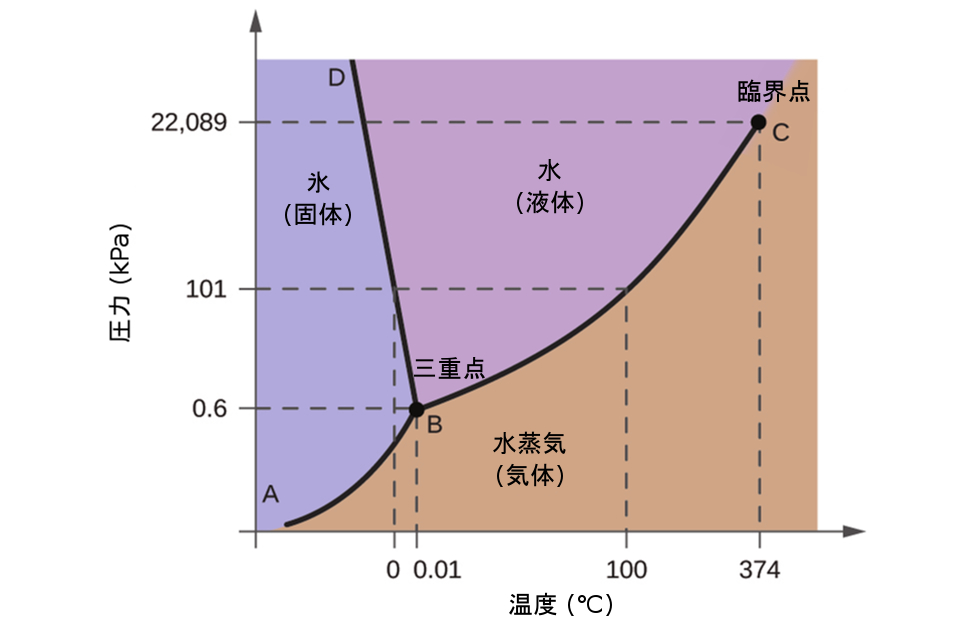
図10.31 | この水についての相図の圧力軸と温度軸は、一定の縮尺で描かれていません(いくつかの重要な性質を説明するためです)。
私たちはこの相図を使って、圧力と温度についての指定された条件下での水の試料の物理状態を特定することができます。たとえば、圧力が50kPa、温度が-10°Cの場合、相図の中で「氷」と表示されている領域に対応します。この条件下では、水は固体(氷)としてしか存在しません。圧力50kPa、温度50°Cでは「水」の領域に対応し、ここでは水は液体としてしか存在しません。圧力25kPa、温度200°Cでは、水は気体の状態でしか存在しません。このH₂O相図では、圧力軸と温度軸は一定の縮尺で描かれていないことに注意してください。これは、ここで記述したようないくつかの重要な特徴を説明できるようにするためです。
図10.31の曲線BCは、この章の前の節で説明した蒸気圧と温度を描画したものです。この「液体-蒸気」曲線は、相図の液体領域と気体領域を分離し、任意の圧力での水の沸点を与えるものです。たとえば、1atmでは、沸点は100°Cです。この液体-蒸気曲線は、温度374 °C、圧力218 atmで終了していることに注意してください。これは、圧力に関係なく、この温度以上では水が液体として存在することができないことを示しています。この条件下での水の物理的性質は、液相と気相の中間的なものです。この独特の物質の状態は超臨界流体と呼ばれ、この節の次の項で説明します。
図10.31でABと表示された固体-蒸気曲線は、氷と水蒸気が平衡にある温度と圧力を示しています。これらの温度-圧力のデータの組は、水の昇華点(凝結点)に対応しています。図10.31の固体-気体の線を拡大して見てみると、氷は-10°Cで約0.20kPaの蒸気圧を持っていることがわかります。したがって、もし私たちが0.20kPa未満の圧力で真空中に凍結した試料を置くと、氷は昇華します。これが、食品の保存によく使われる「凍結乾燥(フリーズドライ)」の基礎となっています(図10.32に示されるアイスクリームのように)。

図10.32 | このアイスクリームのようなフリーズドライ食品は、水の三重点よりも下の圧力で昇華によって脱水されます。(credit: ʺlwaoʺ/Flickr)
BDと表示された固体-液体曲線は、氷と液体の水が平衡にある温度と圧力を示しており、水の融点と凝固点を表しています。この曲線はわずかに負の傾きを示していることに注意してください(わかりやすくするために大きく誇張しています)。これは、圧力が高くなるにつれて水の融点がわずかに低下することを示しています。ほとんどの物質は圧力の上昇に伴って融点が上昇するので、水はこの点では珍しい物質です。この振る舞いは、図10.33に示されるもののような氷河の動きの一端を担っています。氷河の底には、その重さによって巨大な圧力がかかり、氷の一部が融けて液体の水の層ができ、その上では氷河が滑りやすくなっていることがあります。

図10.33 | 氷河の下では膨大な圧力がかかっており、部分的に融けて水の層ができ、この層は氷河の動きを助けるための潤滑を供給します。この衛星写真は、アルゼンチンのペリト・モレノ氷河の先端を示しています。(credit: NASA)
3つの曲線の交点は、図10.31にBで示されています。この点で表される圧力と温度では、水の3つの相はすべて平衡で共存しています。 この温度-圧力のデータの組は三重点と呼ばれます。三重点より低い圧力では、温度に関係なく水は液体として存在することはできません。
例題10.11 水の状態を決定する
図10.31で与えられた水の相図を用いて、以下の温度と圧力での水の状態を決定してください:
(a)−10 °Cおよび50 kPa
(b)25 °Cおよび90 kPa
(c)50 °Cおよび40 kPa
(d)80 °Cおよび5 kPa
(e)−10 °Cおよび0.3 kPa
(f)50 °Cおよび0.3 kPa
解法
水の相図を使うと、私たちは与えられた温度・圧力のそれぞれで水の状態は以下のようになると決定することができます:(a)固体、(b)液体、(c)液体、(d)気体、(e)固体、(f)気体。
学習内容の確認
圧力を0.3kPaに保持した場合、温度が変化するにつれて水はどのような相変化をしますか?また、圧力が50kPaに保持されている場合はどのような相変化をしますか?
解答:0.3kPaの場合:-58 °Cで固体 ⟶ 気体。50 kPaの場合:0 °Cで固体 ⟶ 液体、78 °Cで液体 ⟶ 気体。
もう1つの例として、図10.34に示される二酸化炭素の相図を考えてみましょう。固体-液体曲線は正の傾きを示しており、ほとんどの物質と同様にCO₂の融点が圧力とともに上昇することを示しています(前に説明したように、水は顕著な例外です)。三重点が1atmをはるかに超えていることに注目してください、これは二酸化炭素が常圧条件下では液体として存在できないことを示しています。代わりに、気体の二酸化炭素を1atmで冷却すると、固体状態に凝結します。同様に、固体の二酸化炭素は1atmの圧力では溶けず、代わりに昇華して気体状のCO₂を生成します。最後に、二酸化炭素の臨界点は水に比べて比較的低い温度と圧力で観測されることに注意してください。
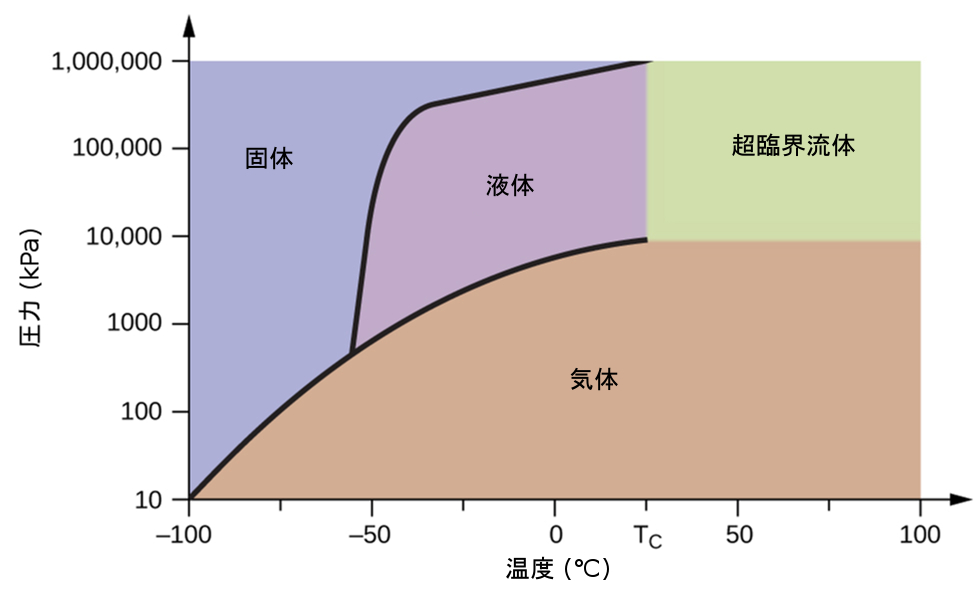
図10.34 | 二酸化炭素の相図が示されています。圧力軸は、大きな値の範囲に対応するために対数スケールで描かれています。
例題10.12 二酸化炭素の状態を決定する
図10.34に示される二酸化炭素の相図を用いて、以下の温度と圧力でのCO₂の状態を決定してください:
(a)−30 °Cおよび2000 kPa
(b)−90 °Cおよび1000 kPa
(c)−60 °Cおよび100 kPa
(d)−40 °Cおよび1500 kPa
(e)0 °Cおよび100 kPa
(f)20 °Cおよび100 kPa
解法
提供された二酸化炭素の相図を使うと、私たちは与えられた温度・圧力のそれぞれでCO₂の状態は以下のようになると決定することができます:(a)液体、(b)固体、(c)気体、(d)液体、(e)気体、(f)気体。
学習内容の確認
圧力を1500kPaで一定に保ちながら、温度を-100°Cから上昇させるときに、二酸化炭素が起こす相変化を特定してください。また、500kPaでも同じことを特定してください。これらの相変化は、おおよそどれくらいの温度で起こりますか?
解答:1500 kPaの場合:-55 °Cで固体 ⟶ 液体、-10 °Cで液体 ⟶ 気体。500 kPaの場合:-60 °Cで固体 ⟶ 気体。
超臨界流体
もし私たちが水の試料を25°Cで密閉容器に入れ、空気を抜き、蒸発-凝縮平衡を確立させると、0.03atmの圧力で液体の水と水蒸気の混合物ができます。密度の高い液体と密度の低い気体の間に明確な境界がはっきりと観察されます。温度を上げると、水の相図(図10.31)の液体-気体曲線によって示されるように、水蒸気の圧力が上昇し、液相と気相の二相平衡が維持されます。温度374°Cでは蒸気圧は218atmまで上昇しており、これ以上温度が上昇すると液相と気相の境界が消失することになります。今や容器内のすべての水は、気体状態と液体状態の中間の物理的性質を持つ単一の相になっています。この物質の相は超臨界流体と呼ばれ、この相が存在するようになる温度と圧力が臨界点となります(図10.35)。臨界温度よりも上では、どれだけ圧力をかけても気体を液化することはできません。臨界温度で気体を液化するのに必要な圧力は、臨界圧力と呼ばれます。いくつかの一般的な物質の臨界温度と臨界圧力が下表に示されています。
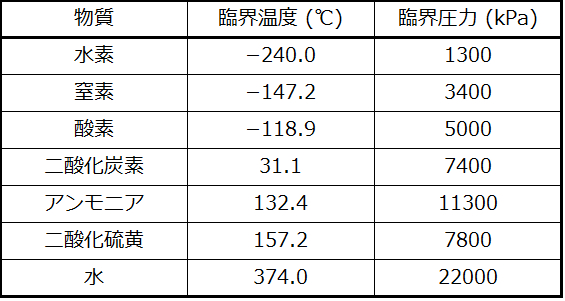
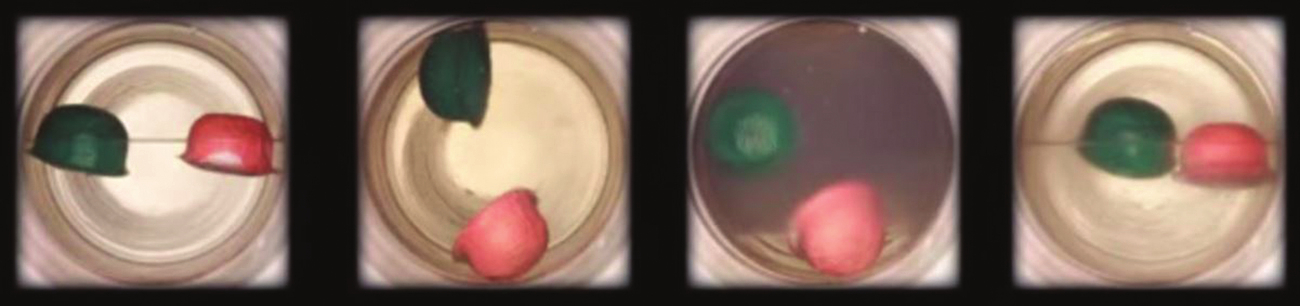
図10.35 | (a)臨界点よりわずかに低い温度の液体の二酸化炭素の密閉容器が加熱されると、(b)超臨界流体相が形成されます。超臨界流体を冷却すると、その温度と圧力が臨界点よりも下に下がり、液体と気体の別々の相(cとd)が再確立されます。色のついたフロートは、液体、気体、超臨界流体の状態の間の密度の違いを示しています。(credit: modification of work by “mrmrobin”/YouTube)
学習へのリンク
二酸化炭素の液体から超臨界流体への転移(http://openstaxcollege.org/l/16supercrit)を観察してください。
気体と同様に、超臨界流体は膨張して容器を満たしますが、その密度は一般的な気体の密度よりもはるかに大きく、一般的には液体の密度に近いです。液体と同様に、これらの流体は不揮発性の溶質を溶解することができます。しかしながら、これらの流体は、基本的に表面張力を示さず、非常に低い粘度を示すので、固体の混合物の非常に小さな開口部をより効果的に貫通し、可溶性成分を除去することができます。これらの性質により、超臨界流体は幅広い用途で非常に有用な溶媒となっています。たとえば、超臨界二酸化炭素は、食品業界で非常に人気のある溶媒であり、コーヒーからカフェインを抜くこと、ポテトチップスから油脂を除去すること、柑橘油から香気成分を抽出することなどに使用されています。それは毒性がなく、比較的安価で、汚染物質とは考えられていません。使用後は、減圧して得られた気体を集めることにより、CO₂を容易に回収することができます。
例題10.13 二酸化炭素の臨界温度
もし私たちが涼しい日(18°C)に二酸化炭素の消火器を振ると、シリンダーの中で液体のCO₂がパチャパチャしている音を聞くことができます。しかしながら、夏の暑い日(35°C)には、同じシリンダーの中には液体が入っていないようです。これらの観察結果を説明してください。
解法
涼しい日には、CO₂の温度はCO₂の臨界温度である304K、すなわち31 °Cよりも下なので(表10.3)、シリンダー内には液体のCO₂が存在しています。暑い日には、CO₂の温度は臨界温度である31 °Cよりも高くなります。この温度よりも上では、いくら圧力をかけてもCO₂を液化させることはできないので、消火器の中には液体のCO₂は存在しません。
学習内容の確認
アンモニアは室温で圧縮することによって液化することができますが、酸素はこのような条件下では液化することができません。2つの気体が異なる振る舞いを示すのはなぜですか?
解答:アンモニアの臨界温度は405.5Kで、室温よりも高いです。酸素の臨界温度は室温よりも低いので、酸素は室温では液化することができません。
日常生活の中の化学
超臨界CO₂を用いたコーヒーの脱カフェイン
コーヒーは石油に次いで世界で2番目に広く取引されている商品です。世界中で、人々はコーヒーの香りと味を愛しています。また、私たちの多くは、朝に活動を始めたり午後に集中を保ったりするのを助けるために、コーヒーの成分であるカフェインに頼っています。しかし、一日の遅い時間になると、コーヒーの刺激作用で眠れなくなることがあるので、夜は脱カフェインのコーヒーを飲むという選択をすることができます。
1900年代初頭以来、コーヒーからカフェインを抜くために多くの方法が使用されています。そのすべてに利点と欠点があり、どれもカフェインの物理的および化学的性質に頼っています。カフェインは、やや極性の分子であるため、それは水(極性の液体)によく溶解します。しかしながら、コーヒーの味と香りに貢献する他の400以上の化合物の多くもまた、H₂Oに溶解するので、熱水での脱カフェインのプロセスはこれらの化合物のいくつかを取り除いてしまうことがあり、カフェイン抜きコーヒーの香りと味に悪影響を与えます。ジクロロメタン(CH₂Cl₂)や酢酸エチル(CH₃CO₂C₂H₅)はカフェインと極性が似ているため、カフェイン抽出に非常に有効な溶媒ですが、どちらもいくつかの風味や香りの成分を除去してしまうとともに、それらの使用には抽出や洗浄に時間がかかります。また、これらの溶媒はいずれも毒性があるため、カフェイン抜きコーヒーに残留する溶媒の健康面での影響が懸念されています。
現在では、二酸化炭素を用いた超臨界流体抽出法が、より効果的で環境に優しい脱カフェイン法として広く利用されています(図10.36)。CO₂は、温度304.2K超、圧力7376kPa超で超臨界流体であり、気体と液体の両方の性質を持ちます。それは気体のようにコーヒー豆の奥深くまで浸透し、液体のように特定の物質を効果的に溶かします。蒸気を当てたコーヒー豆を超臨界二酸化炭素で抽出すると、コーヒーの味と香りの化合物をそのまま残しつつ、カフェインの97~99%が除去されます。CO₂は標準条件下では気体であるため、抽出が行われたコーヒー豆から容易に除去することができ、抽出物からのカフェインの回収も容易です。このプロセスを介してコーヒー豆から回収されたカフェインは、その後、他の食品や医薬品への添加物として利用することができる貴重な生成物です。
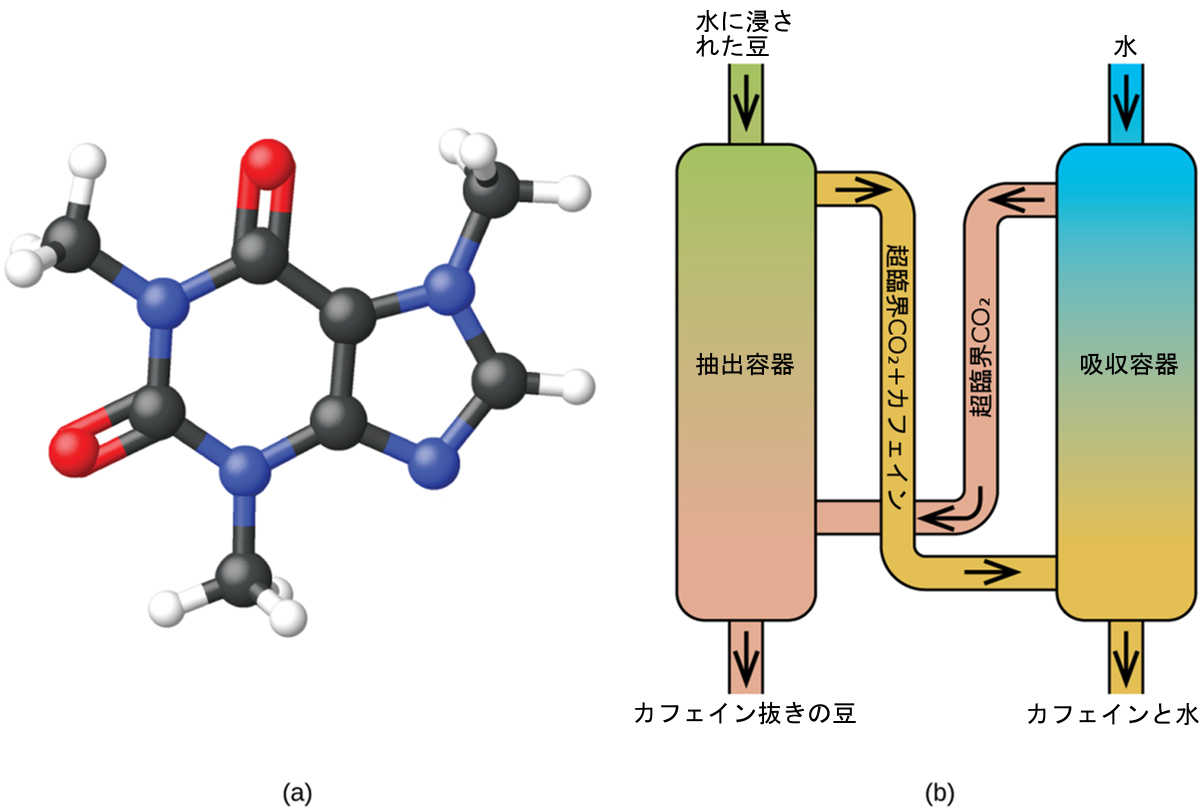
図10.36 | (a)カフェイン分子には極性領域と非極性領域があり、極性の異なる溶媒に対して可溶です。(b)超臨界二酸化炭素を用いた典型的なカフェイン除去プロセスが模式的に示されています。
10.5 物質の固体状態
この節が終わるまでに、あなたは次のことができるようになります:
•イオン性、分子性、金属性、共有結合ネットワーク性といった結晶性固体の結合と性質を定義し、記述する
•結晶性固体の主な種類:イオン性固体、金属性固体、共有結合ネットワーク性固体、分子性固体について記述する
•固体の中で結晶欠陥がどのようにして発生するかを説明する
ほとんどの液体が冷却されるとき、それらは最終的に凍結し、結晶性固体(原子、イオン、または分子が明確な繰り返しパターンで配列されている固体)を形成します。また、その分子が整然としたパターンで配列されるようになる前に液体が凍結することも可能です。このような物質は、非晶質固体または非結晶性固体(または、ときにはガラス)と呼ばれます。このような固体の粒子は、内部構造に秩序がなく、ランダムに配置されています(図10.37)。
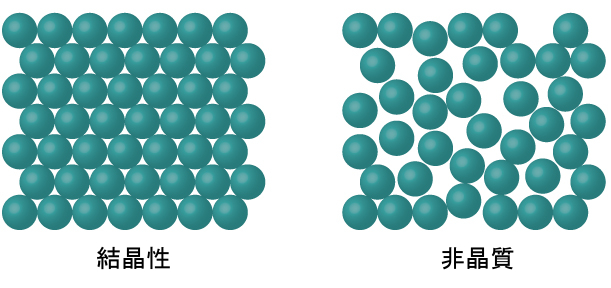
図10.37 | 固相の実体は、規則的で繰り返しのパターンで配置されている場合もあれば(結晶性固体)、ランダムに配置されている場合もあります(非晶質固体)。
金属やイオン化合物は通常、秩序だった結晶性固体を形成します。大きな分子からなる物質、または動きがより制限された分子の混合物は、しばしば非晶質固体を形成します。たとえば、ロウソクのロウは、大きな炭化水素分子からなる非晶質固体です。二酸化ケイ素(図10.38)のようないくつかの物質は、その製造条件によって結晶性固体と非晶質固体のいずれかを形成することができます。また、非晶質固体は、適切な条件下で結晶状態に遷移することがあります。
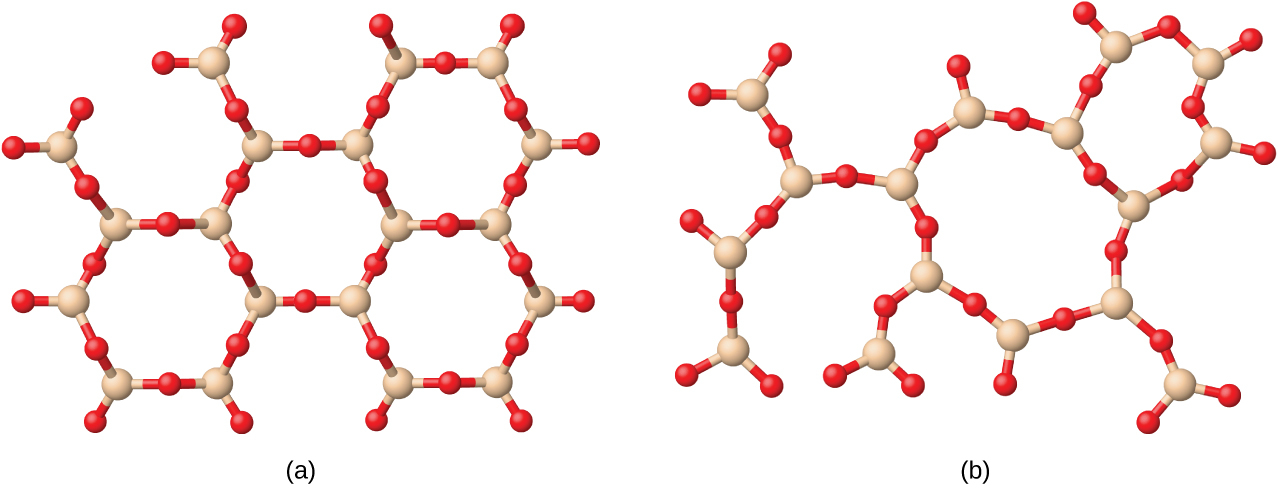
図10.38 | (a)二酸化ケイ素(SiO₂)は、鉱物である石英のいくつかの結晶形態のうちの1つとして自然界に豊富に存在します。(b)溶融したSiO₂を急冷すると、「溶融石英」として知られる非晶質固体が得られます。
結晶性固体は、一般的に粒子をまとめて保持する力の性質に応じて分類されます。これらの力は、バルク固体が示す物理的性質の主な原因となっています。以下の項では、イオン性固体、金属性固体、共有結合ネットワーク性固体、分子性固体といった、結晶性固体の主要なタイプについて説明します。
イオン性固体
塩化ナトリウムや酸化ニッケルなどのイオン性固体は、陽イオンと陰イオンからなり、それらのイオンは静電引力によってまとめて保持されています。静電引力は非常に強くなることがあります(図10.39)。また、多くのイオン性結晶は高い融点を有しています。これはイオン間の非常に強い引力によるものです。イオン化合物では、完全電荷間の引力は、極性分子化合物の部分電荷間の引力よりも(はるかに)大きいです。これについては、後ほど格子エネルギーについての議論の中で詳しく見ていきます。イオン性固体は硬いですが、脆い傾向があり、曲がるというよりは砕けてしまいます。イオン性固体は電気を通しません。しかしながら、溶融したり溶解したりするとイオンが自由に動くようになるので電気を通します。金属元素と非金属元素が反応して形成された単純な化合物の多くはイオン性です。
図10.39 | 塩化ナトリウムはイオン性固体です。
金属性固体
銅、アルミニウム、鉄の結晶のような金属性固体は、金属原子によって形成されています(図10.40)。金属性結晶の構造は、しばしば非局在化した電子の「海」の中に原子核が一様に分布しているものとして表現されることがあります。このような金属性固体の中の原子は、金属結合として知られている独特な力によってまとめて保持されており、この力は多くの有用で多様なバルク特性を生み出しています。それらはすべて高い熱伝導率と電気伝導率、金属光沢、および展性を示します。多くは非常に硬く、非常に強いです。金属性固体は、その展性(圧力やハンマーで叩いたときに変形する能力)のために、砕けることがなく、それゆえに有用な建築材料となります。さまざまな金属の融点は大きく異なります。水銀は室温では液体であり、アルカリ金属は200°C未満で融けます。いくつかのポスト遷移金属も低い融点を持っていますが、遷移金属は1000°C超の温度で溶融します。これらの違いは、金属間の金属結合の強さの違いを反映しています。
図10.40 | 銅は金属性固体です。
共有結合ネットワーク性固体
共有結合ネットワーク性固体には、ダイヤモンド、ケイ素、他のいくつかの非金属、および二酸化ケイ素(砂)や炭化ケイ素(紙やすりの研磨材であるカーボランダム)のようないくつかの共有結合化合物の結晶が含まれます。多くの鉱物は共有結合のネットワークを持っています。図10.41に示されるように、これらの固体の原子は共有結合のネットワークによってまとめて保持されています。共有結合ネットワーク性固体を破壊したり融かしたりするには、共有結合を破壊しなければなりません。共有結合は比較的強いため、共有結合ネットワーク性固体は、典型的には、硬く、強く、高い融点を特徴とします。たとえば、ダイヤモンドは既知の最も硬い物質の1つであり、3500 °C超で融解します。
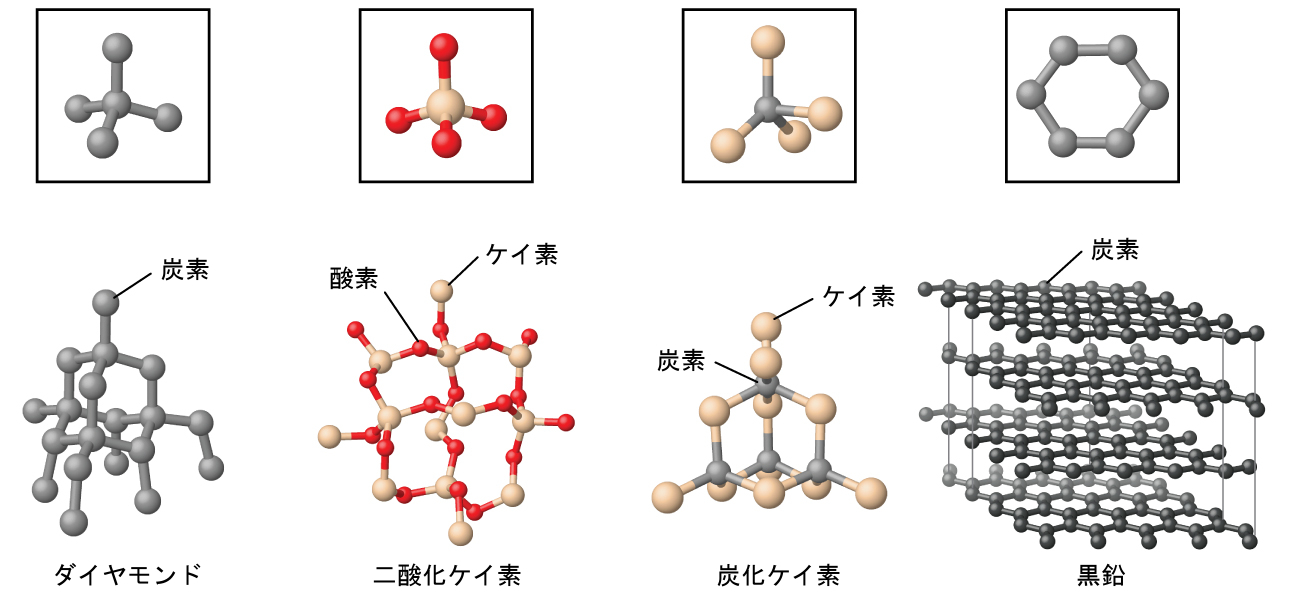
図10.41 | 共有結合性結晶は、ダイヤモンド、二酸化ケイ素、炭化ケイ素、黒鉛の構造で示されるように、共有結合の三次元ネットワークを含んでいます。黒鉛は例外的な例で、非共有結合の力によって層状に保持された共有結合性結晶の平面的なシートで構成されています。典型的な共有結合性固体とは異なり、黒鉛は非常に柔らかく、電気伝導性があります。
分子性固体
図10.42に示されるように、氷、スクロース(食卓の砂糖)、ヨウ素などの分子性固体は、中性分子で構成されています。さまざまな結晶中に存在する単位間の引力の強さは大きく異なります。これは、それぞれの結晶の融点によって示されます。H₂、N₂、O₂、F₂のような小さな対称分子(非極性分子)は弱い引力を持ち、非常に低い融点(-200 °C未満)の分子性固体を形成します。より大きな非極性分子からなる物質は、より大きな引力を持ち、より高い温度で融解します。永久双極子モーメントを持つ分子(極性分子)からなる分子性固体は、さらに高温で融解します。例としては、氷(融点0°C)や食卓の砂糖(融点185°C)などが含まれます。
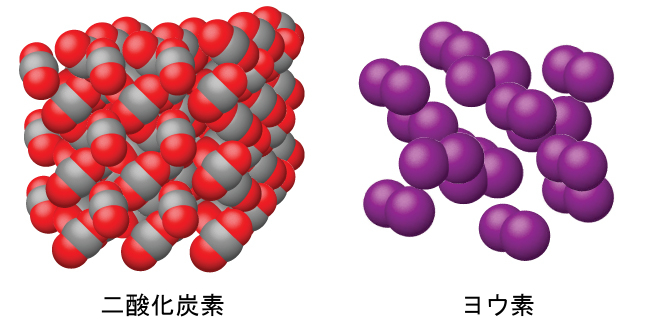
図10.42 | 二酸化炭素(CO₂)は、小さな非極性分子からなり、融点-78 °Cの分子性固体を形成します。ヨウ素(I₂)は、より大きな非極性分子で構成され、114°Cで融解する分子性固体を形成します。
固体の性質
表10.4に記載されているような結晶性固体は、精度の高い融解温度を有しています。なぜなら、同じ種類の原子または分子のそれぞれが同じ力またはエネルギーで定位置に保持されており、したがって、結晶を構成する単位間の引力はすべて同じ強さを持ち、破壊するためにはすべて同じ量のエネルギーを必要とするからです。非晶質物質が緩やかに軟化していくことは、結晶性固体が明確に融解することとは大きく異なります。これは、非晶質固体中の分子の構造的な非等価性に起因しています。いくつかの力は他のものよりも弱いものであり、非晶質材料が加熱されると、最も弱い分子間引力が最初に破壊されます。温度がさらに増加すると、より強い引力が破壊されます。このように非晶質材料は温度の範囲にわたって柔らかくなっていきます。
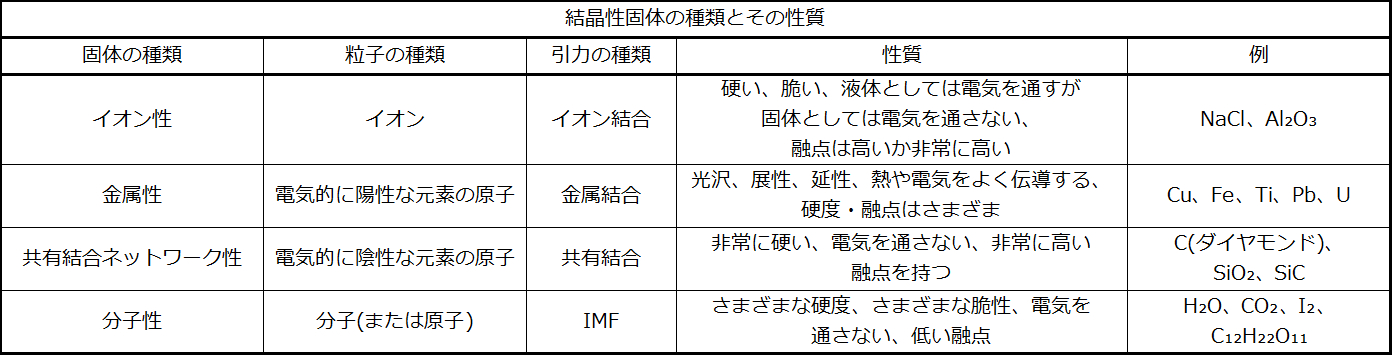
表10.4
さまざまな科学のつながり
グラフェン:未来の素材
炭素は私たちの世界に欠かせない元素です。炭素原子が持つ独特の性質により、私たち自身のような炭素系生命体の存在が可能となっています。炭素は、図10.43に示されるようなものを含め、私たちが日常的に使用しているさまざまな物質を形成しています。あなたは、炭素の最も一般的な2つの同素体であるダイヤモンドと黒鉛のことをよく知っているかもしれません。(同素体とは、同じ元素の異なる構造的形態のことです。)ダイヤモンドは既知の最も硬い物質の1つですが、黒鉛は鉛筆の芯として使用されるほど柔らかい物質です。このように非常に異なる性質を持つのは、異なる同素体の中での炭素原子の配列の違いに起因しています。
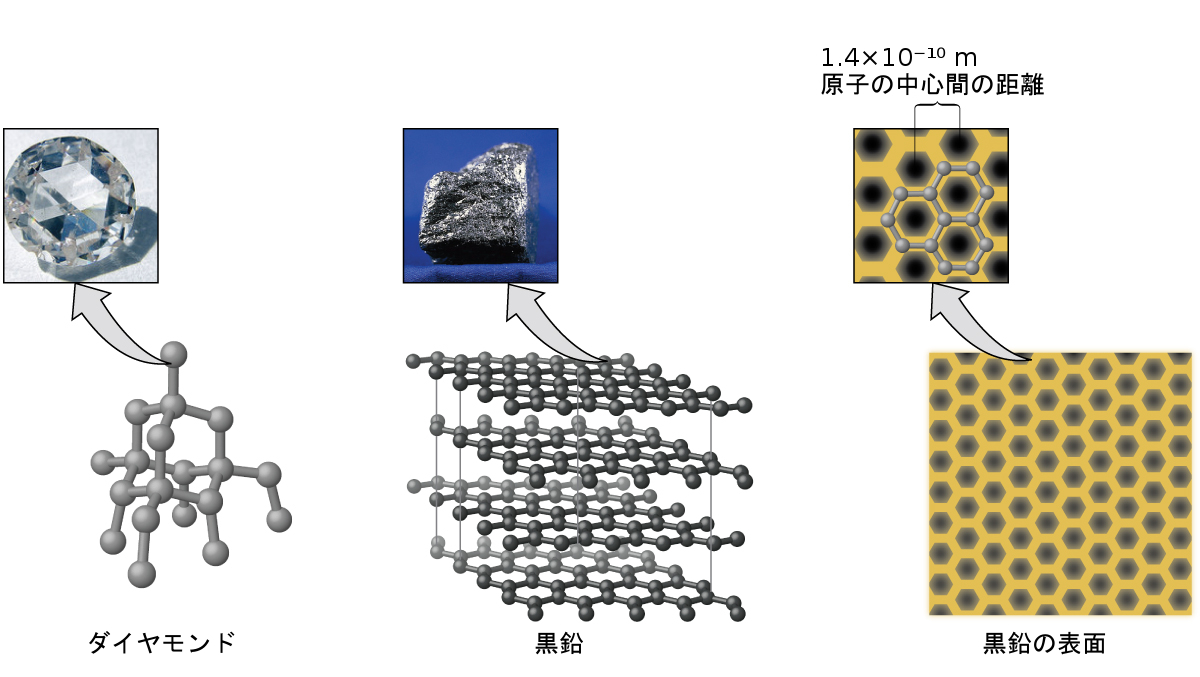
図10.43 | ダイヤモンドが非常に硬いのは、あらゆる方向の炭素原子の間で強い結合があるからです。黒鉛(鉛筆の芯)が紙の上でこすり落とされて付着するのは、炭素層間の弱い引力のためです。黒鉛の表面の画像は、隣り合う炭素原子の中心間の距離を示しています。(credit left photo: modification of work by Steve Jurvetson; credit middle photo: modification of work by United States Geological Survey)
あなたは、最近発見された炭素の一形態であるグラフェンについては、あまりなじみがないかもしれません。グラフェンは2004年に、テープを使って黒鉛からどんどん薄い層をはがすことで初めて単離されました。グラフェンは、本質的には一枚のシート(原子1個分の厚さ)の黒鉛です。図10.44に示されるように、グラフェンは強くて軽いだけでなく、電気や熱の優れた伝導体でもあります。これらの性質は、コンピュータのチップや回路の大幅な改良、電池や太陽電池の高性能化、構造材料の高強度化・軽量化など、さまざまな用途で非常に有用であることが実証される可能性があります。2010年のノーベル物理学賞は、グラフェンについての先駆的な研究により、アンドレ・ガイムとコンスタンチン・ノボセロフに授与されました。
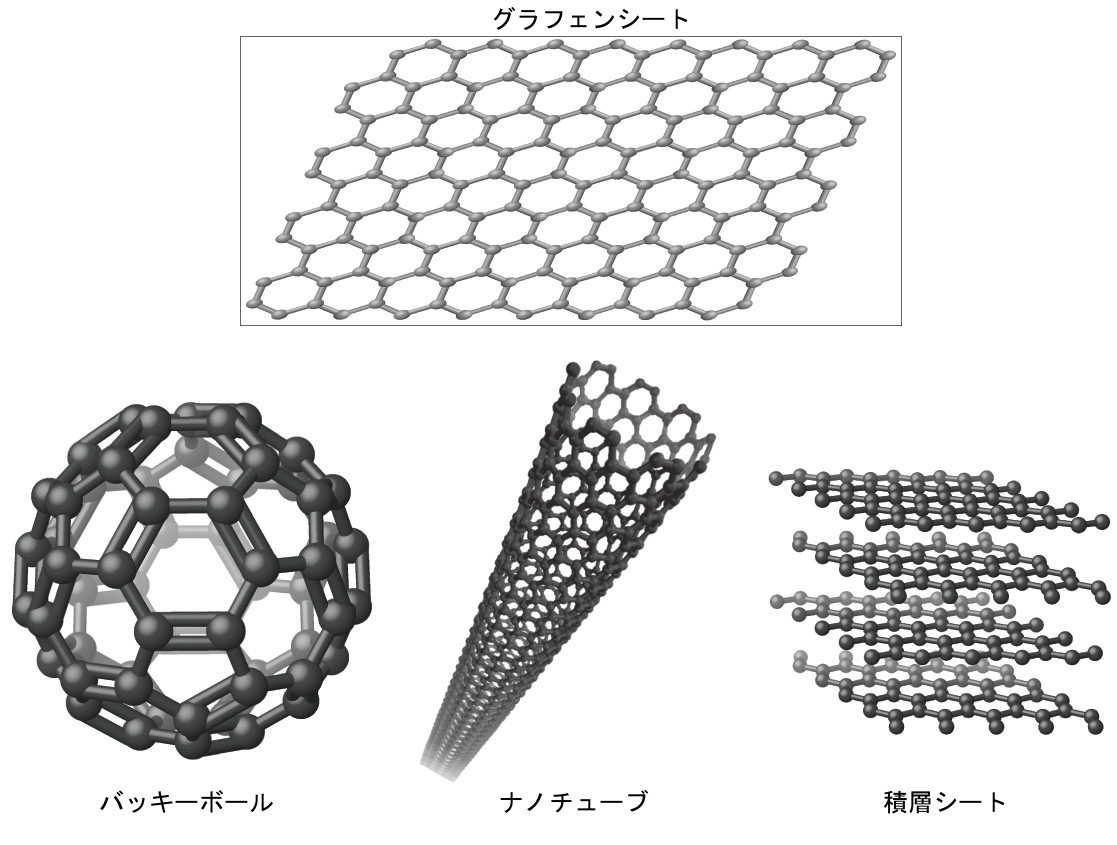
図10.44 | グラフェンのシートは、バッキーボール、ナノチューブ、積層体などに形成することができます。
結晶欠陥
結晶性固体では、原子、イオン、または分子は明確な繰り返しパターンで配置されていますが、時にはパターン内に欠陥が発生することがあります。図10.45に示されるように、いくつかの種類の欠陥が知られています。空孔とは、原子やイオンを含むはずの位置が空になっている場合に発生する欠陥です。あまり一般的ではありませんが、結晶中におけるいくつかの原子やイオンが、原子の通常の位置の間にある格子間サイトと呼ばれる位置を占めることがあります。他の歪みは、不純な結晶で見られます(たとえば、不純物のカチオン、アニオン、または分子が大きすぎて、構造を歪めずに規則的な位置に収まらない場合など)。結晶の性質に望ましい変化をもたらす欠陥を構造の中に作り出すために、微量の不純物が結晶に添加されることがあります(ドーピングとして知られているプロセス)。たとえば、シリコン結晶には、半導体やコンピュータチップの製造に使用するのに適した電気的性質を得るために、さまざまな量の異なる元素がドープされます。
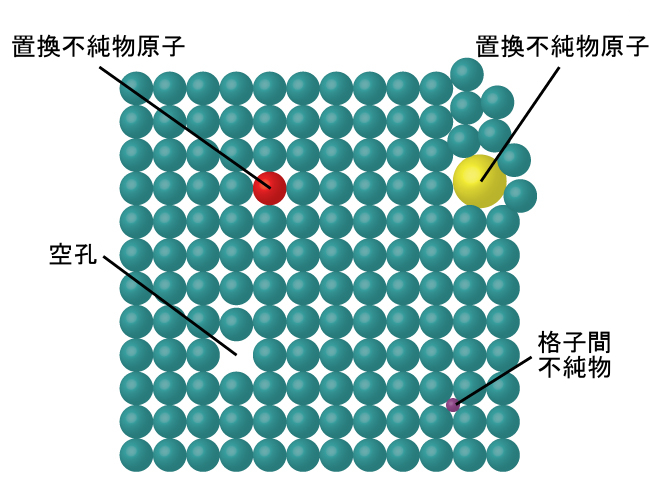
図10.45 | 結晶欠陥の種類には、空孔、格子間原子、置換不純物などがあります。
10.6 結晶性固体の格子構造
この節が終わるまでに、あなたは次のことができるようになります:
•結晶構造における原子とイオンの配置を記述する
•単位胞の寸法を用いてイオン半径を計算する
•結晶構造を決定する際にX線回折測定を使用することを説明する
自然界に存在する固体と人工的に作られた固体の90%超は結晶性です。ほとんどの固体は、その粒子の規則的な配列で形成されます。なぜなら、粒子が最も効率的な形で充填されるときには、粒子間の全体的な引力の相互作用が最大化され、分子間エネルギーの合計が最小化されるからです。原子レベルでの規則的な配列は、しばしば巨視的なレベルに反映されています。この節では、金属性およびイオン性の結晶性固体の構造についての詳細を探り、これらの構造がどのようにして実験的に決定されるかを学びます。
金属の構造
私たちは、元素金属について考えることから結晶性固体の議論を始めることにしましょう。元素金属は、それぞれが1種類の原子を含むために、比較的単純なものです。純金属とは、金属原子が繰り返しパターンで密に詰まった結晶性固体のことです。展性や延性などといった金属の一般的な性質の一部は、同一の原子が規則的なパターンで配列されていることに大部分は起因するものです。ある金属の性質が、他の金属と比較して異なっているのは、部分的にはその原子の大きさや空間的な配置の特殊性に基づいています。私たちは、以下の項の中で、最も一般的な金属結晶の幾何構造のうちの4つについての類似点と相違点を探っていきます。
金属の単位胞
金属であろうとなかろうと、結晶性固体の構造は、その最も単純な繰り返し単位(その単位胞と呼ばれます)を考慮することによって記述するのが最適です。単位胞は、原子やイオンの位置を表す格子点で構成されています。図10.46に示されるように、全体の構造は、この単位胞が三次元的に繰り返されることによって構成されています。
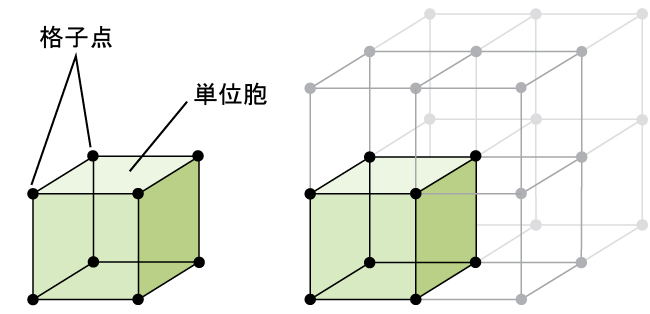
図10.46 | 単位胞は、全方向に繰り返される格子点の位置を示します。
最も簡単な構造と最も基本的な単位胞から、結晶の格子構造と単位胞の調査を始めましょう。これを視覚化するには、まずテニスボールのような同じ球体を大量に手に取り、容器の中に一様に並べることを想像してみてください。これを行うための最も単純な方法は、図10.47に示されているように、ある1つの層の球体が下の層の球体の直上にあるようにして層を重ねていくことでしょう。このような配置は単純立方構造と呼ばれ、単位胞は単純立方単位胞または基本立方単位胞と呼ばれます。
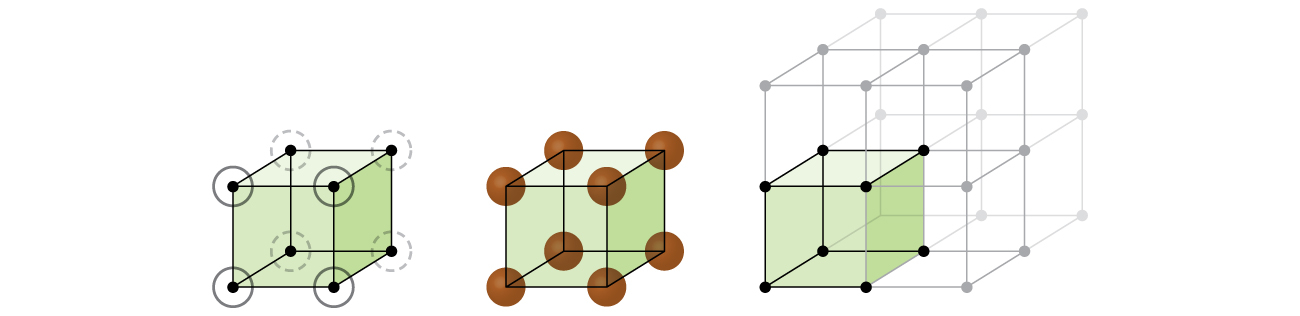
図10.47 | ある層の球体が別の層の球体の真上または真下に配置されるようにして金属原子が配列されている場合、格子構造は単純立方構造と呼ばれます。球体同士は接触していることに注意してください。
単純立方構造では、球体は、本来可能なほどには密に詰め込まれていません。それらは容器の体積の約52%だけを「充填」しています。これは比較的に非効率的な配置であり、たった1つの金属(ポロニウム、Po)のみが単純立方構造で結晶化します。図10.48に示されるように、この種類の配置を持つ固体は、平面(または層)から構成されます。それぞれの原子は、同じ層にある4つの最も近い隣接原子、上の層において真上にある1つの原子、下の層において真下にある1つの原子と接触します。結晶性固体中のそれぞれの粒子が接触する他の粒子の数は、粒子の配位数として知られています。したがって、単純立方配列のポロニウム原子の場合、配位数は6です。
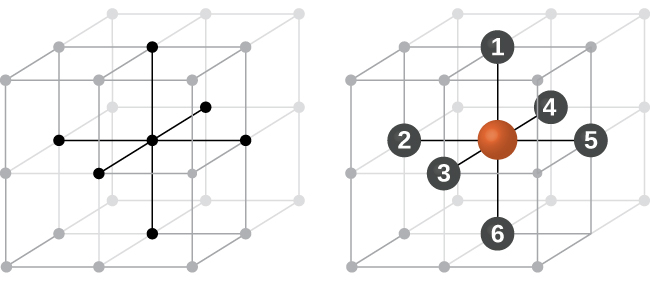
図10.48 | 単純立方格子構造の中にある1つの原子は、他の6つの原子と接触しているので、その配位数は6です。
図10.49に示されるように、単純立方格子では、すべての方向に繰り返される単位胞は、8つの原子の中心によって定義される立方体です。この単位胞の隣接する角にある原子は互いに接触しているので、この単位胞の一辺の長さは2原子半径、つまり1原子直径に相当します。立方体の単位胞には、その中に入っているいくつかの原子の一部分だけが含まれています。単純立方単位胞の角にある原子は、合計8個の単位胞に含まれているので、ある特定の単位胞にはその原子の8分の1だけが含まれていることになります。そして、単純立方構造のそれぞれの単位胞は、その8つの「角」にそれぞれ1つの原子を持っているので、1つの単純立方単位胞内には、8 × 1/8 = 1つの原子が存在します。
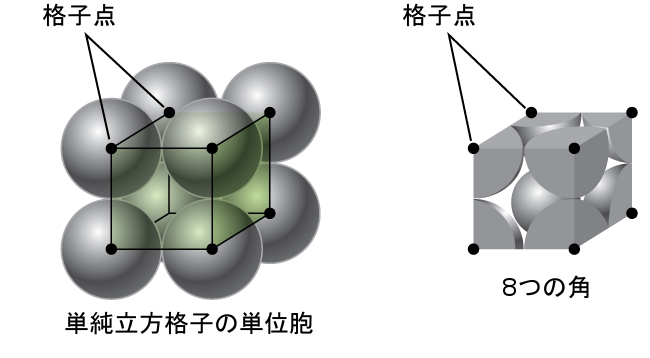
図10.49 | 単純立方格子の単位胞には、8つの角にそれぞれ8分の1の原子が含まれているので、合計で1つの原子が含まれていることになります。
例題10.14 金属の原子半径と密度の計算、その1
αポロニウムの単位胞の一辺の長さは336pmです。
(a)ポロニウム原子の半径を決定してください。
(b)αポロニウムの密度を決定してください。
解法
αポロニウムは単純立方単位胞で結晶化します:
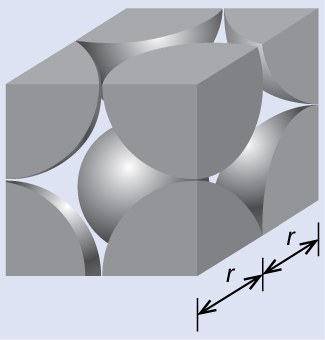
(a)2つの隣接するPo原子が互いに接触するので、この単位胞の一辺の長さは、2つのPo原子の半径に等しいです:l = 2r。したがって、Poの半径は、以下のようになります。
\[ r = \frac{l}{2} =\rm \frac{336\ pm}{2}= 168\ pm \]
(b)密度は密度 = 質量/体積で与えられます。ポロニウムの密度は、その単位胞の密度(単位胞内に含まれる質量を単位胞の体積で割ったもの)を決定することによって求めることができます。ポロニウムの単位胞は、その8つの角のそれぞれに8分の1個のPo原子を含んでいるため、1つの単位胞には1つのPo原子が含まれています。
Po単位胞の質量は以下のように求めることができます:
\[ \rm 1\ Po 単位胞 ×\frac{1\ Po 原子}{1\ Po 単位胞}×\frac{1\ mol\ Po}{6.022 × 10^{23}\ Po 原子}×\frac{208.998\ g}{1\ mol\ Po}= 3.47 × 10^{−22}\ g \]
Po単位胞の体積は以下のように求めることができます:
\[ V = l^3 =\rm (336 × 10^{−10}\ cm)^3= 3.79 × 10^{−23}\ cm^3 \]
(密度についての通常の体積単位を得るために、辺の長さをpmからcmに変換したことに注意してください。)
したがって、Poの密度は:
\[ \rm Poの密度 =\frac{3.471 × 10^{−22}\ g}{3.79 × 10^{−23}\ cm^3}= 9.16\ g/cm^3 \]
学習内容の確認
ニッケルの単位胞の一辺の長さは0.3524nmです。ニッケルの密度は8.90g/cm³です。ニッケルは単純立方構造で結晶化するでしょうか?説明してください。
解答:いいえ。もしニッケルが単純立方構造であれば、その密度は以下で与えられるでしょう:
\[ {\rm 1\ Ni原子×\frac{1\ mol\ Ni}{6.022 × 10^{23}\ Ni原子}×\frac{58.693\ g}{1\ mol\ Ni}= 9.746 × 10^{−23}\ g}\\ V = l^3 = {\rm (3.524 × 10^{−8}\ cm)^3= 4.376 × 10^{−23}\ cm^3} \]
そうすると、Niの密度は以下のようになるでしょう:
\[ {\rm Niの密度 =\frac{9.746 × 10^{−23}\ g}{4.376 × 10^{−23}\ cm^3}= 2.23\ g/cm^3} \]
Niの実際の密度はこれに近いものではないので、Niは単純立方構造を形成しません。
ほとんどの金属結晶は、単位胞の4つの主要なタイプのうちの1つです。ここでは、私たちは、単純立方単位胞(すでに見てきました)、体心立方単位胞、面心立方単位胞という3つの立方単位胞に焦点を当てます。これらはすべて図10.50に示されています。(実際には7つの異なる格子系があり、そのうちのいくつかは複数のタイプの格子を持ち、合計14種類の異なる種類の単位胞があることに注意してください。より複雑な幾何構造については、この節で後述します。)
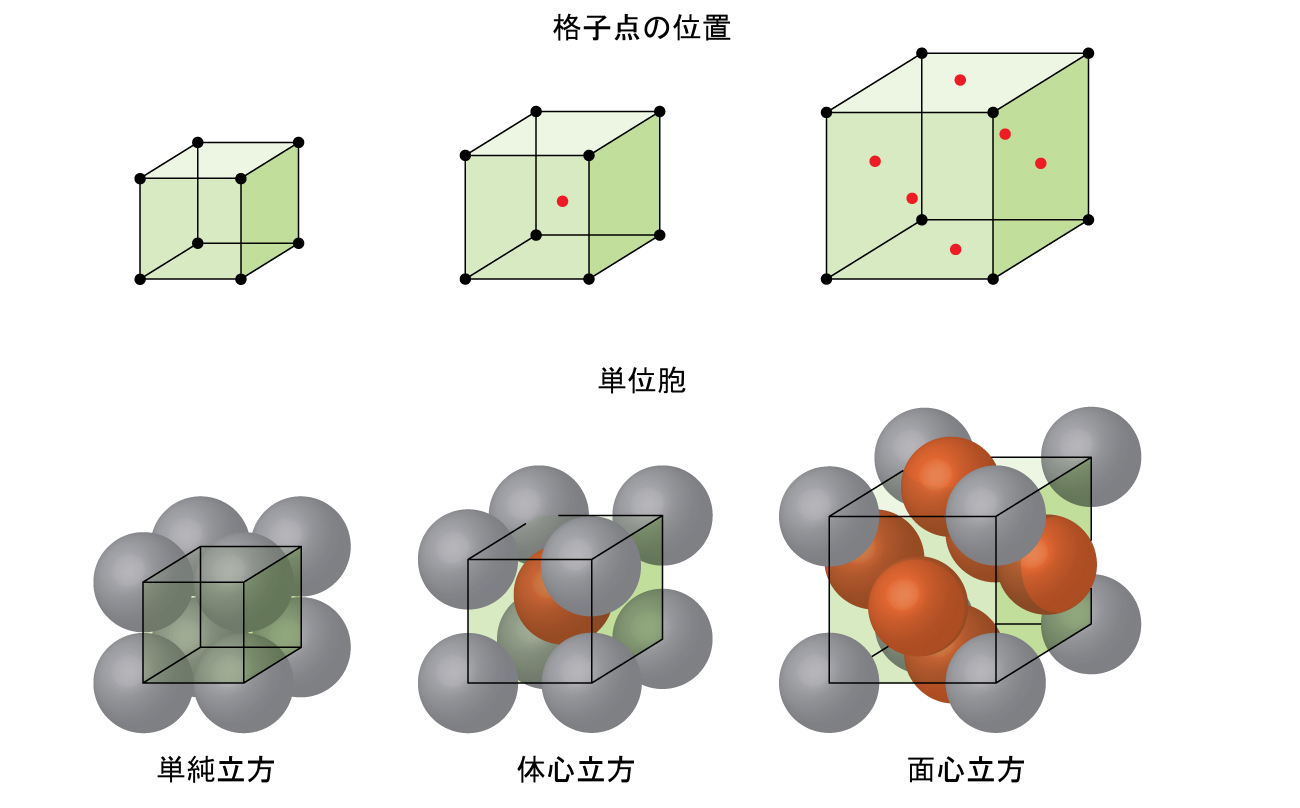
図10.50 | これらの金属の立方単位胞は、格子点の位置(上の図)、および単位胞内にある金属原子(下の図)を示しています。
図10.51に示されるように、いくつかの金属は、すべての角に原子があり、中心に1つの原子があるような立方単位胞を有する配置で結晶化します。これを体心立方(BCC)固体と呼びます。BCC単位胞の角にある原子はお互いには接触せず、中心にある原子に接触します。BCC単位胞には2つの原子が含まれています:8つの角のそれぞれにある8分の1個の原子(8 × 1/8 = 1原子が角にあります)と、中心にある1個の原子です。この構造の中のどの原子も、その上の層にある4つの原子とその下の層にある4つの原子に接触しています。したがって、BCC構造の原子の配位数は8となります。
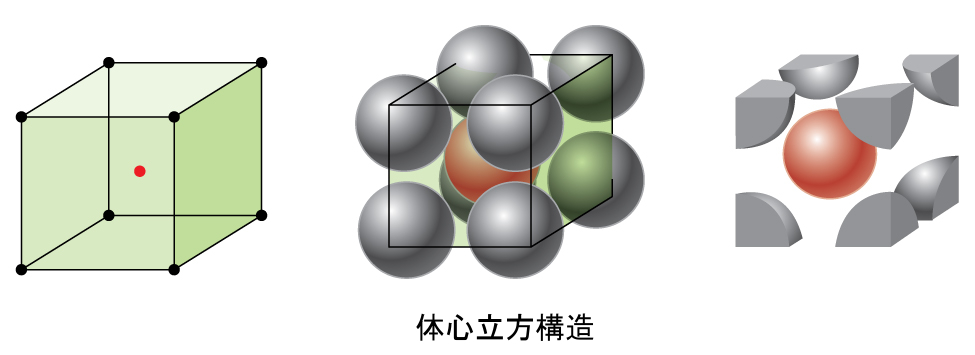
図10.51 | 体心立方構造では、ある特定の層にある原子は互いに接触しません。それぞれの原子は、その上の層にある4つの原子とその下の層にある4つの原子に接触します。
BCC配列の原子は、単純立方構造の原子よりもはるかに効率的に充填されており、全体積の約68%を占めています。BCC構造を持つ同形金属としては、室温でのK、Ba、Cr、Mo、W、Feなどがあります。(同じ構造で結晶化した元素や化合物を同形といいます。)
図10.52に示されるように、アルミニウム、銅、鉛などの他の多くの金属は、すべての角とそれぞれの面の中心に原子があるような立方単位胞を有する配置で結晶化します。この配置を面心立方(FCC)固体と呼びます。FCC単位胞には4つの原子が含まれています:8つの角のそれぞれにある1/8個の原子(8 × 1/8 = 1原子が角にあります)と、6つの面のそれぞれにある1/2個の原子(6 × 1/2 = 3原子が面にあります)です。角にある原子は、立方体の面の対角線に沿って隣接する面の中心にある原子に接触します。どの原子も同じ格子点上にあるので、それらは同じ環境を持っています。
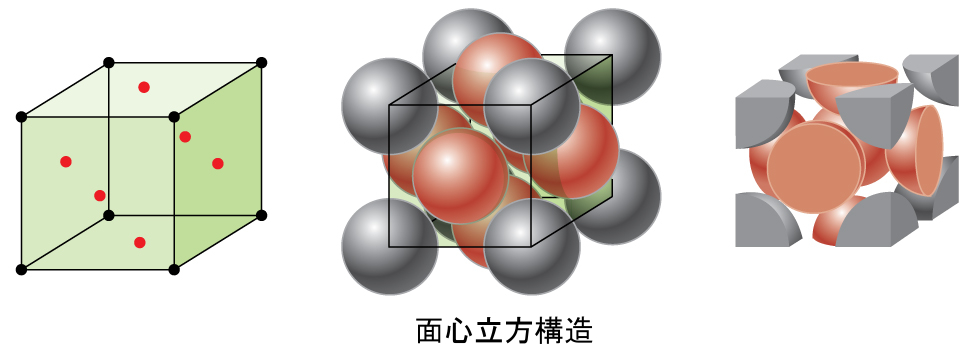
図10.52 | 面心立方固体は、それぞれの角に原子があるとともに、その名前が示す通り、単位胞の面の中心にも原子があります。
FCC配置における原子は可能な限り近接して詰めこまれており、体積の74%を原子が占めています。この構造は、立方最密充填(CCP)とも呼ばれています。CCPでは、六角形に配置された原子の3つの繰り返し層があります。それぞれの原子は、自身の層にある6個の原子、上の層にある3個の原子、下の層にある3個の原子に接触します。この配置では、それぞれの原子は12個の近傍の原子に接触しているので、その配位数は12です。FCC配列とCCP配列が等価であるという事実はすぐには明白ではないかもしれませんが、それらが実際になぜ同じ構造なのかは図10.53に示されています。
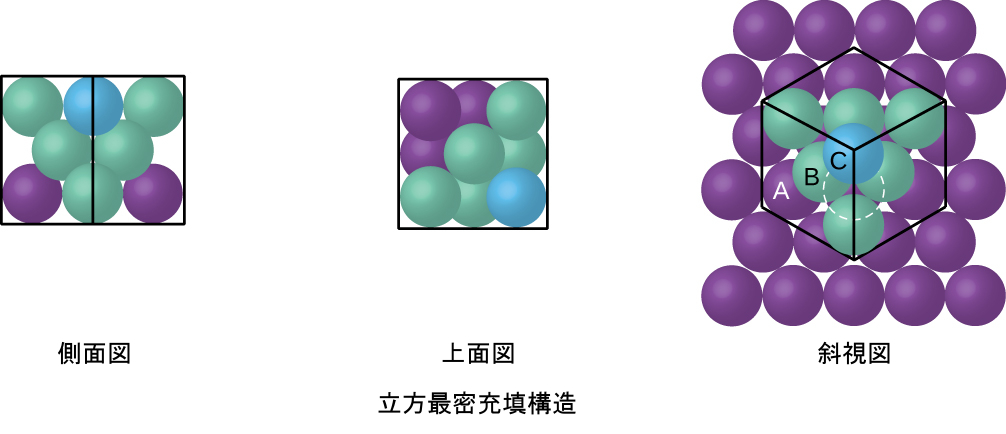
図10.53 | CCP配置は、六角形に配置された原子の3つの繰り返し層(ABCABC…)で構成されています。CCP構造の原子は、自身の層にある6つの原子に加えて、上の層にある3つの原子と下の層にある3つの原子と接触しているので、配位数は12となります。視点を回転させてみると、CCP構造は、面(1つの角にA層の原子を含み、対角線に沿って(2つの角と面の中央に)B層の原子を含み、残りの角にC層の原子を含む)からなる単位胞を持っていることがわかります。これは、面心立方配置と同じです。
より近接して充填することで原子間の全体的な引力が最大化され、合計の分子間エネルギーが最小化されるため、ほとんどの金属の原子はこのやり方で充填されます。私たちは、単純な金属結晶構造において、2つのタイプの最密充填を見つけることができます:1つはすでに見たCCPであり、もう1つは図10.54に示される六方最密充填(HCP)です。どちらも六角形に配置された原子の繰り返し層で構成されています。どちらのタイプでも、第一の層(A)の上に第二の層(B)が配置され、第二の層にあるそれぞれの原子が第一の層にある3つの原子と接触するようになっています。第三の層は、2つのうちのいずれかの方法で配置されます。HCPでは、第三の層の原子は、第一の層の原子の真上にあり(すなわち、第三の層もA型です)、その積層は、A型とB型の最密層を交互に積層する(すなわち、ABABAB…)ように構成されます。CCPでは、第三の層の原子は、第一の層・第二の層のいずれの原子の真上にもなく(すなわち、第三の層はC型です)、その積層は、A型、B型、およびC型の最密層を交互に積層する(すなわち、ABCABCABC…)ように構成されます。すべての金属のうち約3分の2は、配位数12の最密充填配列で結晶化します。HCP構造で結晶化する金属にはCd、Co、Li、Mg、Na、Znがあり、CCP構造で結晶化する金属にはAg、Al、Ca、Cu、Ni、Pb、Ptがあります。
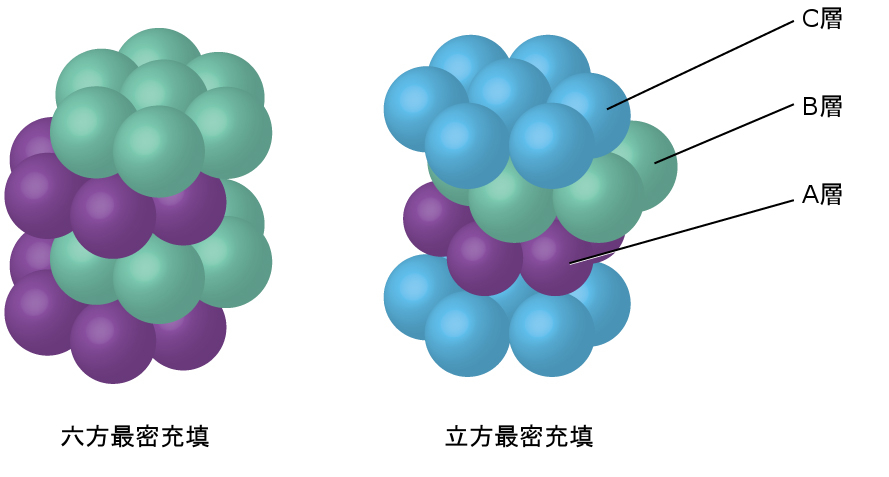
図10.54 | いずれのタイプの最密充填でも、原子は可能な限りコンパクトに充填されています。六方最密充填は、2つの交互の層(ABABAB…)で構成されています。立方最密充填は3つの交互の層(ABCABCABC…)で構成されています。
例題10.15 金属の原子半径と密度の計算、その2
カルシウムは面心立方構造で結晶化します。その単位胞の一辺の長さは558.8pmです。
(a)この構造におけるCaの原子半径は何ですか?
(b)Caの密度を計算してください。
解法
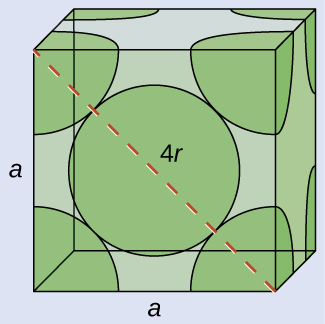
(a)FCC構造では、面の対角線に沿ってCa原子が接触しているので、対角線の長さは4つのCa原子半径 (d=4r) に等しいです。隣接する2つの辺と面の対角線とは直角三角形を形成し、それぞれの辺の長さは558.8pm、斜辺の長さは4つのCa原子半径に等しくなります:
\[ a^2 + a^2 = d^2 ⟶{\rm (558.8\ pm)^2 +(558.5\ pm)^2} = (4r)^2 \]
これを解くと、以下が得られます
\[ r ={\rm \sqrt{\frac{(558.8\ pm)^2 +(558.5\ pm)^2}{16}}= 197.6\ pm} \]
これがCaの半径です。
(b)密度は密度 = 質量/体積で与えられます。カルシウムの密度は、その単位胞の密度を決定することによって求めることができます:たとえば、単位胞内に含まれる質量を単位胞の体積で割ったものです。面心立方構造のCaの単位胞は、8つの角のそれぞれに8分の1個の原子(8 × 1/8 = 1個の原子)、6つの面のそれぞれに2分の1個の原子(6 × 1/2 = 3個の原子)があり、合計4つの原子が単位胞に含まれていることになります。
単位胞の質量は以下のように求めることができます:
\[ {\rm 1 Ca 単位胞×\frac{4\ Ca 原子}{1\ Ca 単位胞}×\frac{1\ mol\ Ca}{6.022 × 10^{23}\ Ca 原子}×\frac{40.078\ g}{1\ mol\ Ca}= 2.662 × 10^{−22}\ g} \]
Ca単位胞の体積は以下のように求めることができます:
\[ V = a^3 ={\rm (558.8 × 10^{−10}\ cm)^3= 1.745 × 10^{−22}\ cm^3} \]
(密度についての通常の体積単位を得るために、辺の長さをpmからcmに変換したことに注意してください。)
したがって、Caの密度は:
\[ \rm Caの密度 =\frac{2.662 × 10^{−22}\ g}{1.745 × 10^{−22}\ cm^3}= 1.53\ g/cm^3 \]
学習内容の確認
銀はFCC構造で結晶化します。その単位胞の一辺の長さは 409 pm です。
(a)この構造におけるAgの原子半径は何ですか?
(b)Agの密度を計算してください。
解答:(a)144 pm、(b)10.5 g/cm³
図10.55に示されるように、一般的に、ある1つの単位胞は、3つの軸(a、b、c)の長さとそれらの間の角度(α、β、γ)によって定義されます。軸は、空間格子内の点の間の長さとして定義されます。したがって、単位胞の軸は、同じ環境にある点を結びます。
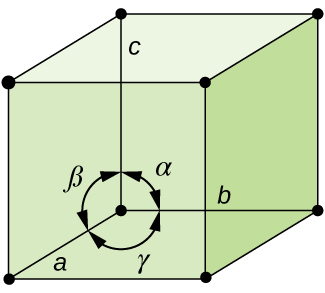
図10.55 | ある1つの単位胞は、その3つの軸(a、b、c)の長さと軸の間の角度(α、β、γ)によって定義されます。
7つの異なる格子系があり、その中には2種類以上の格子を持つものもあり、合計14種類の異なる単位胞があります。それらは、図10.56に示されるような形状をしています。
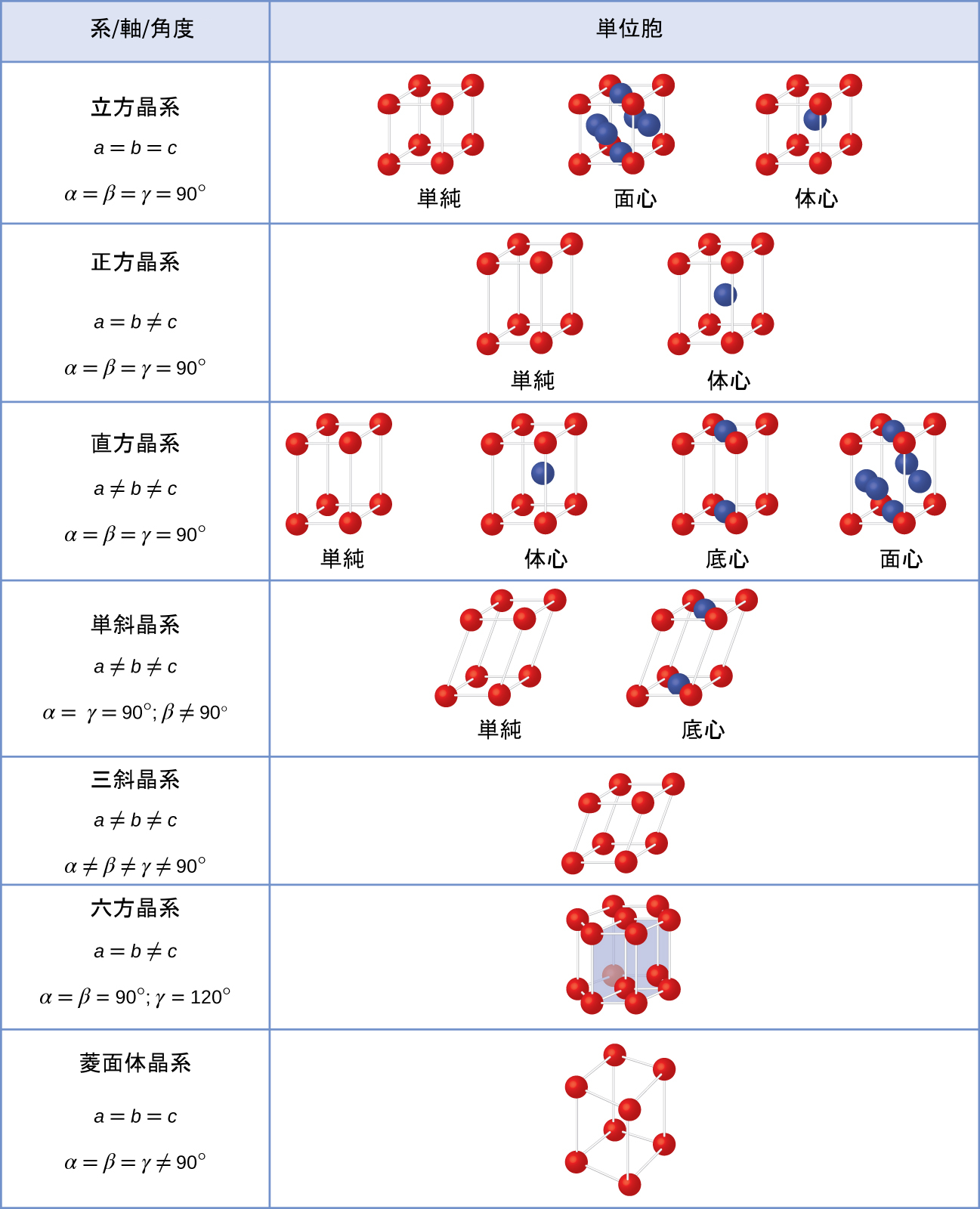
図10.56 | 7つの異なる格子系と14種類の単位胞があります。
イオン性結晶の構造
イオン性結晶は、2つかそれ以上の異なる種類のイオンで構成されています。そのイオンは、通常は異なるサイズを持ちます。これらのイオンの結晶構造への充填は、金属原子(同じサイズを持っています)の充填よりも複雑です。
ほとんどの単原子イオンは電荷を帯びた球体として振る舞い、それらが反対の電荷を帯びたイオンへ及ぼす引力はどの方向であっても同じです。その結果、イオン化合物の安定な構造は、(1)ある電荷のイオンが、可能な限り多くの反対の電荷のイオンに囲まれているとき、および、(2)カチオンとアニオンがお互いに接触しているときに得られます。構造は、イオンの相対的な大きさと、化合物中の陽イオンと陰イオンの数の比率という2つの主要な要因によって決定されます。
単純なイオン構造では、アニオン(通常、カチオンよりも大きいです)が最密充填配置されるように配列されています。(前に見たように、ある原子核から形成される原子と比べると、同じ原子核に引き寄せられる電子が増えればアニオンは大きくなり、同じ原子核に引き寄せられる電子が減ればカチオンは小さくなります。)小さいカチオンは、一般的に、アニオンの間に残っている2種類の正孔(または間隙)のうちの1つを占めています。小さい方の正孔は、ある平面にある3つのアニオンと、隣接する平面にある1つのアニオンの間にあります。この正孔を囲む4つのアニオンは四面体の角に配置されているので、この正孔は四面体孔と呼ばれています。これよりも大きなタイプの正孔は、八面体の角にある6つのアニオン(ある層にある3つと、隣接する層にある3つ)の中心にあり、これは八面体孔と呼ばれます。図10.57は、これらの種類の正孔の両方を示しています。
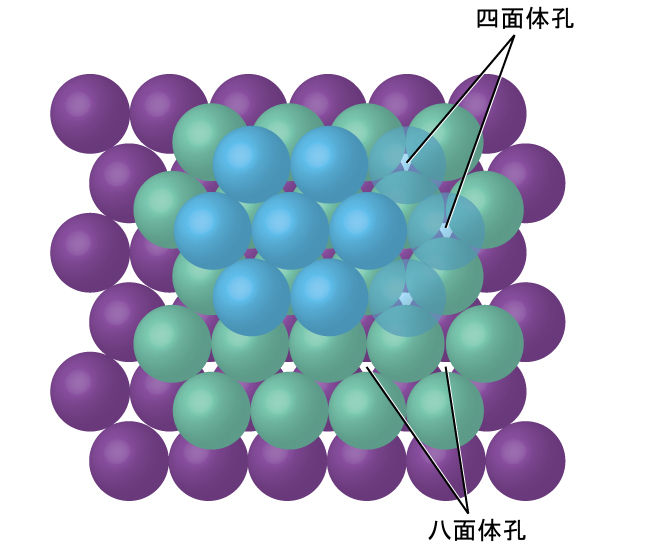
図10.57 | カチオンは、アニオンの間にある八面体孔と四面体孔という2種類の正孔を占めることがあります。
図10.58に示されるように、イオン化合物のカチオンは、カチオンとアニオンの相対的な大きさに応じて、四面体孔または八面体孔を占めることがあります。比較的小さいカチオンは四面体孔を占め、大きいカチオンは八面体孔を占めます。もしカチオンが大きすぎて八面体孔に収まらない場合には、アニオンは単純立方配列のようなより広がった構造をとることがあります。そこでは、より大きなカチオンは、より広がった間隔によって可能となった、より大きな立方体孔を占有することができます。
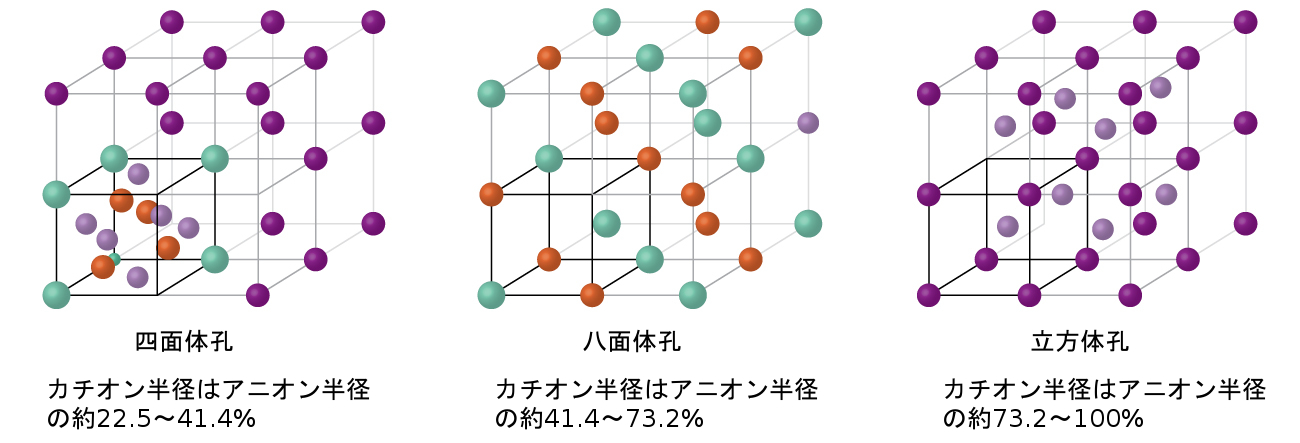
図10.58 | カチオンの大きさと化合物が占める正孔の形状は直接関係しています。
アニオンがHCP配列またはCCP配列のいずれかである場合には、それぞれのアニオンに対して2つの四面体孔があります。アニオンが最密充填配列で結晶化し、カチオンが四面体孔に入る化合物は、最大で2:1のカチオン:アニオンの比率を有することができます。この比率ではすべての四面体孔が充填されます。例としては、Li₂O、Na₂O、Li₂S、およびNa₂Sが含まれます。2:1未満の比率を有する化合物もまた、アニオンが最密充填配列で結晶化し、カチオンが四面体孔内に入ることができます(イオンサイズが適合する場合には)。しかしながら、これらの化合物では、四面体孔の一部が空孔のままです。
例題10.16 四面体孔の占有率
硫化亜鉛は亜鉛の重要な工業的供給源であり、塗料の白色顔料としても使用されています。硫化亜鉛は、硫化物イオンが最密充填された配列で、亜鉛イオンが四面体孔の2分の1を占める状態で結晶化します。硫化亜鉛の化学式は何ですか?
解法
アニオン(硫化物イオン)1個につき四面体孔が2個あり、それらの正孔の半分が亜鉛イオンによって占められているため、硫化物イオン1個につき1/2 × 2、つまり1個の亜鉛イオンが存在しなければなりません。したがって、化学式はZnSとなります。
学習内容の確認
セレン化リチウムは、セレン化物イオンが最密充填配列であり、四面体孔のすべてにリチウムイオンが入っていると表現することができます。セレン化リチウムの化学式は何ですか?
解答:Li₂Se
HCP構造またはCCP構造においては、八面体孔とアニオンの比率は1:1です。したがって、アニオンが最密充填配列であり、カチオンが八面体孔に入る化合物は、最大で1:1のカチオン:アニオンの比率を有することができます。たとえば、NiO、MnS、NaCl、およびKHでは、八面体孔はすべて充填されています。一部の八面体孔が空のままの場合には、1:1未満の比率が観察されます。
例題10.17 イオン化合物の化学量論
サファイアは酸化アルミニウムです。酸化アルミニウムは、酸化物イオンが最密充填された配列で、アルミニウムイオンが八面体孔の3分の2に入った状態で結晶化します。酸化アルミニウムの化学式は何ですか?
解法
アニオン(酸化物イオン)1個につき、八面体孔が1個あり、それらの正孔の3分の2が占有されているので、アルミニウムと酸素の比率は2/3:1でなければならず、これはAl2/3Oを与えることになります。最も単純な整数比は2:3であるため、化学式はAl₂O₃となります。
学習内容の確認
白色の顔料である酸化チタンは、酸化物イオンが最密充填された配列で、チタンイオンが八面体孔の2分の1に入った状態で結晶化します。酸化チタンの化学式は何ですか?
解答:TiO₂
アニオンが単純な立方体配列の場合では、配列中のそれぞれのアニオンに対してカチオンが占有することができる1つの立方体孔が存在します。CsClや同じ構造を持つ他の化合物では、すべての立方体孔が占有されています。SrH₂、UO₂、SrCl₂、CaF₂では、立方体孔の半分が占有されています。
イオンの相対的な大きさと化学量論(構造を決定する2つの主要な特徴)が似ている場合、異なる種類のイオン化合物が同じ構造で結晶化することがしばしばあります。
イオン化合物の単位胞
多くのイオン化合物は立方体の単位胞で結晶化しています。私たちは、これらの化合物を用いてイオン性構造の一般的な特徴を記述していきます。
あるイオン化合物が、同じような大きさのカチオンとアニオン(1:1の比率)で構成されている場合、それは典型的には単純立方構造を形成しています。塩化セシウム(CsCl)(図10.59に図示)はその一例で、Cs⁺は174 pm、Cl⁻は181 pmの半径を持っています。私たちは、塩化物イオンが単純な立方体の単位胞を形成しており、セシウムイオンがその中心にあると考えることができます。または、セシウムイオンが単位胞を形成しており、塩化物イオンがその中心にあると考えることもできます。さらにまた、Cs⁺イオンによって形成された単純な立方体の単位胞が、Cl⁻イオンによって形成された単位胞に重なっているとも考えることができます。セシウムイオンと塩化物イオンは、単位胞の対角線に沿って接触します。1つの単位胞あたりに1つのセシウムイオンと1つの塩化物イオンが存在し、塩化セシウムの化学式で必要とされる1:1の化学量論を与えます。単位胞の中心には格子点がないこと、セシウムイオンは塩化物イオンと同一ではないのでCsClはBCC構造ではないことに注意してください。
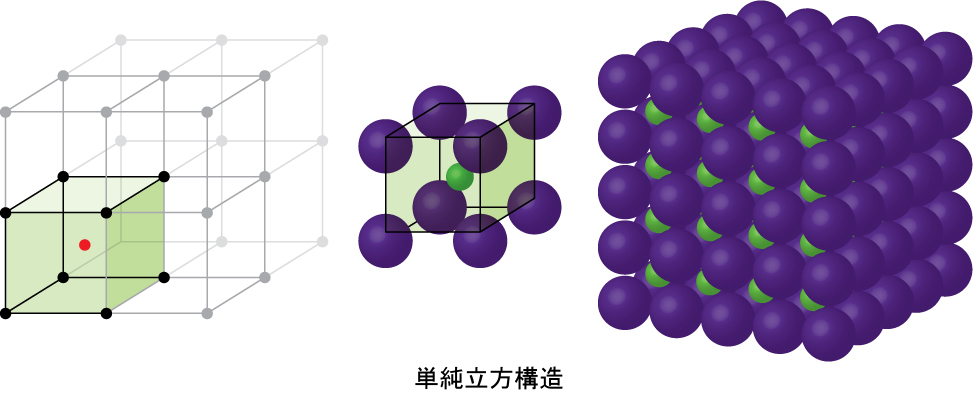
図10.59 | CsClのように似たようなサイズのカチオンとアニオンを持つイオン化合物は、通常、単純立方構造を形成します。これらの化合物は、角にカチオンを持つ単位胞、または角にアニオンを持つ単位胞のいずれかによって記述することができます。
私たちは、格子点の位置は任意であると述べました。これは、CsCl構造の代替的な記述によって説明されます。そこでは、格子点がセシウムイオンの中心に位置しています。この記述では、セシウムイオンは単位胞の角の格子点上に配置され、塩化物イオンは単位胞の中心に配置されています。2つの単位胞は異なりますが、同一の構造を記述しています。
あるイオン化合物が、大きさのまったく異なるカチオンとアニオン(1:1の比率)で構成されている場合、それは典型的には図10.60に示されるようなFCC単位胞で結晶化します。塩化ナトリウム(NaCl)はその一例で、Na⁺は102 pm、Cl⁻は181 pmの半径を持っています。私たちは、塩化物イオンがFCC単位胞を形成しており、ナトリウムイオンが単位胞の辺の真ん中と単位胞の中心にある八面体孔に位置していると考えることができます。ナトリウムイオンと塩化物イオンは、単位胞の辺に沿って互いに接触しています。単位胞には4つのナトリウムイオンと4つの塩化物イオンが含まれており、化学式(NaCl)によって必要とされる1:1の化学量論が得られます。
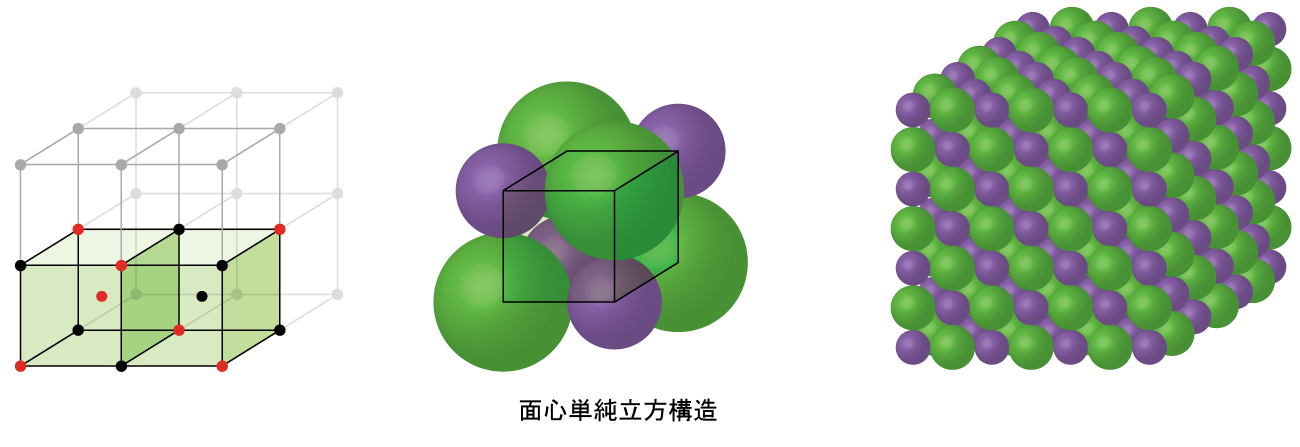
図10.60 | NaClのようにカチオンよりもはるかに大きなアニオンを持つイオン化合物は、通常、FCC構造を形成します。これらの化合物は、八面体孔にカチオンを持つFCC単位胞によって記述することができます。
図10.61に示されるように、硫化亜鉛の立方形態である閃亜鉛鉱もFCC単位胞で結晶化します。この構造は、FCC格子の格子点上に硫化物イオンを含んでいます。(硫化物イオンの配置は塩化ナトリウムにおける塩化物イオンの配置と同じです。)亜鉛イオンの半径は硫化物イオンの半径の40%程度しかないので、これらの小さなZn²⁺イオンは四面体孔に交互に位置します(すなわち四面体孔のうちの半分に入ります)。単位胞には4つの亜鉛イオンと4つの硫化物イオンが存在し、経験式ZnSを与えます。
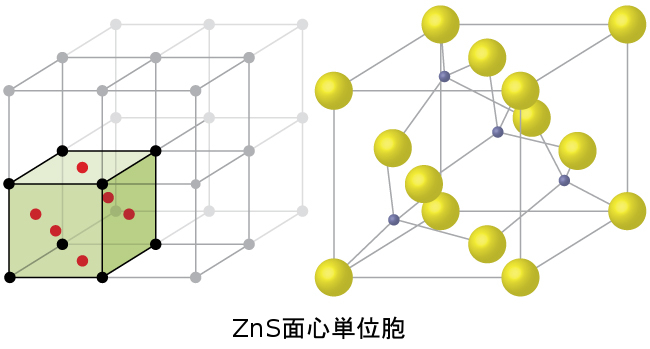
図10.61 | ZnS(硫化亜鉛または閃亜鉛鉱)は、硫化物イオンが格子点にあり、はるかに小さい亜鉛イオンが構造内の四面体孔の半分を占めているようなFCC単位胞を形成します。
図10.62に示されるもののようなフッ化カルシウム単位胞もまたFCC単位胞ですが、この場合では、カチオンが格子点に位置しています。同等のカルシウムイオンはFCC格子の格子点に位置しています。カルシウムイオンのFCC配列の四面体サイトの全てがフッ化物イオンによって占められています。単位胞内に4つのカルシウムイオンと8つのフッ化物イオンがあり、化学式CaF₂で必要とされる1:2のカルシウム:フッ素比率を与えます。図10.62の詳細図は、単純立方配列のフッ化物イオンと立方体孔の半分を占めるカルシウムイオンを明らかにします。この構造は、フッ化物イオンがすべて同一の環境を持っているわけではないので、フッ化物イオンの点の空間格子の観点から記述することはできません。また、フッ化物イオンの周りの4つのカルシウムイオンの配向も異なります。
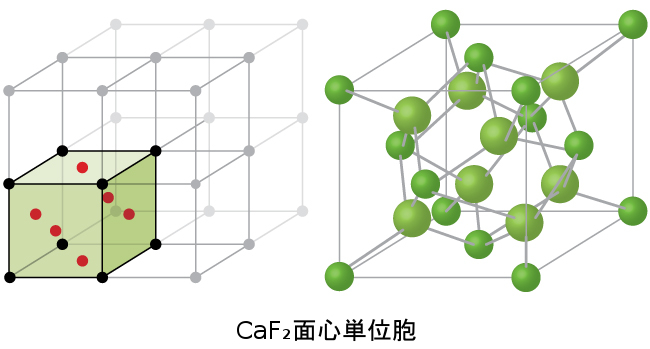
図10.62 | フッ化カルシウムCaF₂は、カルシウムイオン(緑色)が格子点にあり、フッ化物イオン(赤色)がそれらの間の四面体サイトのすべてを占めるようなFCC単位胞を形成します。
イオン半径の計算
もし私たちがイオン化合物の単位胞の辺の長さと単位胞内のイオンの位置を知っており、個々のイオンの形状や接触について仮定を行うならば、化合物に含まれるイオンのイオン半径を計算することができます。
例題10.18 イオン半径の計算
LiCl(NaClに似た構造、FCC)の単位胞の辺の長さは0.514 nm(または5.14Å)です。図10.60のようにリチウムイオンが小さく、塩化物イオンが接触していると仮定して、塩化物イオンのイオン半径を計算してください。
注:長さの単位オングストローム(Å)は原子スケールの寸法を表すのにしばしば使われ、10⁻¹⁰m に相当します。
解法
LiCl単位胞の表面では、塩化物イオンが表面の対角線上で互いに接触しています:
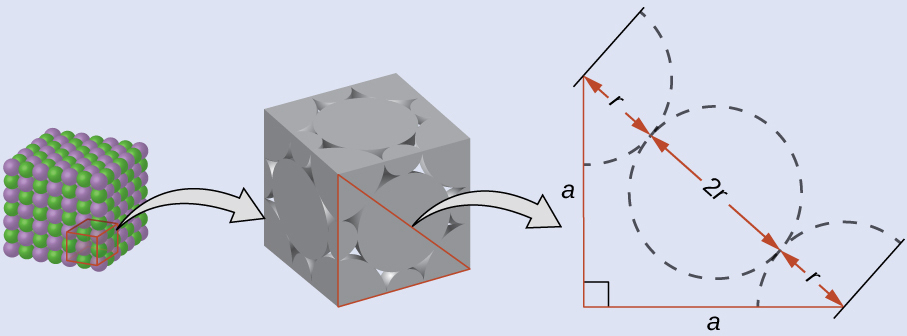
単位胞の面に直角三角形を描くと、対角線の長さが4つの塩化物イオン半径(それぞれの角の塩化物イオンからの半径1つずつと、面の中心にある塩化物イオンからの1つの直径(2つの半径に等しいです))に等しいことがわかりますので、d = 4r。ピタゴラスの定理から、次のようになります:
\[ a^2 + a^2 = d^2 \]
これにより、以下が得られます:
\[ {\rm (0.514\ nm)^2 + (0.514\ nm)^2} = (4r)^2 = 16r^2 \]
これを解くと:
\[ r =\rm \sqrt{\frac{(0.514\ nm)^2 + (0.514\ nm)^2}{16}}=0.182\ nm\ (1.82\ Å) \]
これがCl⁻の半径です。
学習内容の確認
KCl(NaClに似た構造、FCC)の単位胞の辺の長さは6.28Åです。単位胞の辺に沿ってアニオンとカチオンが接触していると仮定して、カリウムイオンの半径を計算してください。塩化物イオンの半径は1.82Åです。
解答:カリウムイオンの半径は1.33Åです。
単位胞の辺の長さから計算されたイオン半径の値は、イオンが完全な球形であるといったような多くの仮定(それはせいぜい近似的なものです)に依存していることを理解しておくことが重要です。したがって、そのような計算値はそれ自体が近似値であり、比較を過度に押し進めることはできません。それでも、この方法は、X線結晶構造解析による決定のような実験的測定からイオン半径を計算するのに有用であることが証明されています。
X線結晶構造解析
単位胞の大きさや結晶内での原子の配置は、結晶によるX線の回折の測定から決定されることがあります。これは、X線結晶構造解析と名付けられています。回折とは、電磁波がその光の波長の大きさに匹敵する大きさの物理的な障壁に遭遇したときに、電磁波の進行方向が変化することです。X線は、結晶中の隣り合う原子間の距離と同じくらいの長さ(数Åのオーダー)の波長を持つ電磁放射です。
単色のX線のビームが結晶に当たると、結晶内の原子によって全方位に散乱されます。同じ方向に飛んだ散乱波が互いにぶつかると、干渉を起こします。干渉とは、波が組み合わさるプロセスのことで、組み合わさる波の最大値がどの程度離れているかによって振幅(強度)が大きくなったり小さくなったりするものです(図10.63参照)。
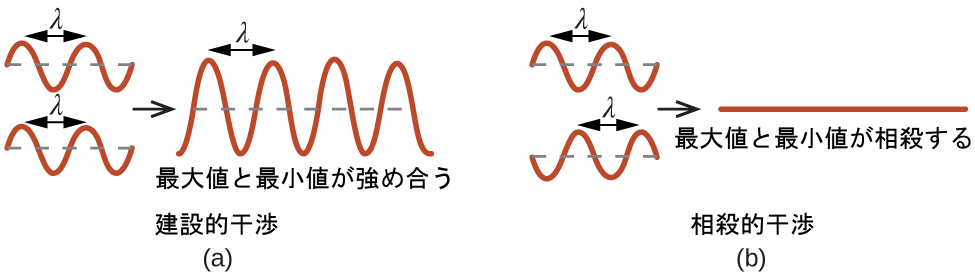
図10.63 | 同じ空間を占有している光の波が干渉を起こし、その最大値と最小値がどれだけ離れているかに応じて、強度の大きい(a)または小さい(b)波が得られます。
ある波長λのX線が、距離dで隔てられた隣接する結晶面の原子によって散乱される場合、それらは、組み合わさる前の2つの波が移動した距離の差が波長の整数因子n倍であるときに、建設的干渉を受けることがあります。この条件は、回折されたビームの角度θが、以下の式によって波長と原子間距離とに関係しているときに満たされます:
\[ nλ= 2d\ {\rm sinθ} \]
この関係は、この現象を最初に説明したイングランドの物理学者W・H・ブラッグにちなんで、ブラッグ方程式として知られています。図10.64は、同じ2つの結晶面からの回折波の2つの例を示しています。上の図はブラッグ角で回折した波が建設的干渉を起こしているところを描いているのに対し、下の図はブラッグ条件を満たさない異なる角度で回折した波が相殺的干渉を起こしているところを示しています。
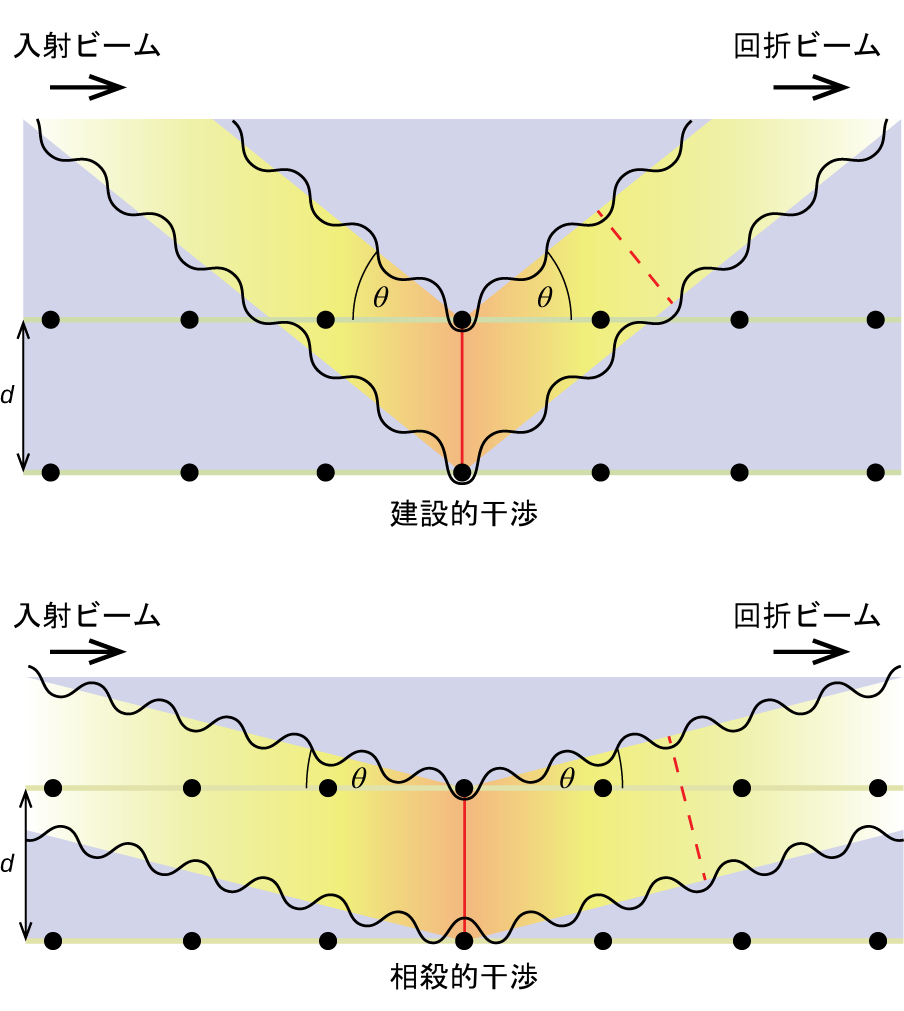
図10.64 | 結晶中の原子によって散乱されたX線の回折により、原子間の距離を決定することができます。上の図は、2つの散乱波の間の建設的干渉と、結果として生じる高強度の回折波を示しています。下の図は、相殺的干渉と低強度の回折波を示しています。
学習へのリンク
ブラッグ方程式の詳細や、回折波の強度に対するそれぞれの変数の影響を調べることができるシミュレータについては、このサイト(http://openstaxcollege.org/l/16bragg)を訪れてみてください。
図10.65に示されるもののようなX線回折計は、前述のように結晶と相互作用したときにX線が回折する角度を測定するために使用することができます。以下の例題で示すように、このような測定値から、ブラッグ方程式を使用して原子間の距離を計算することができます。
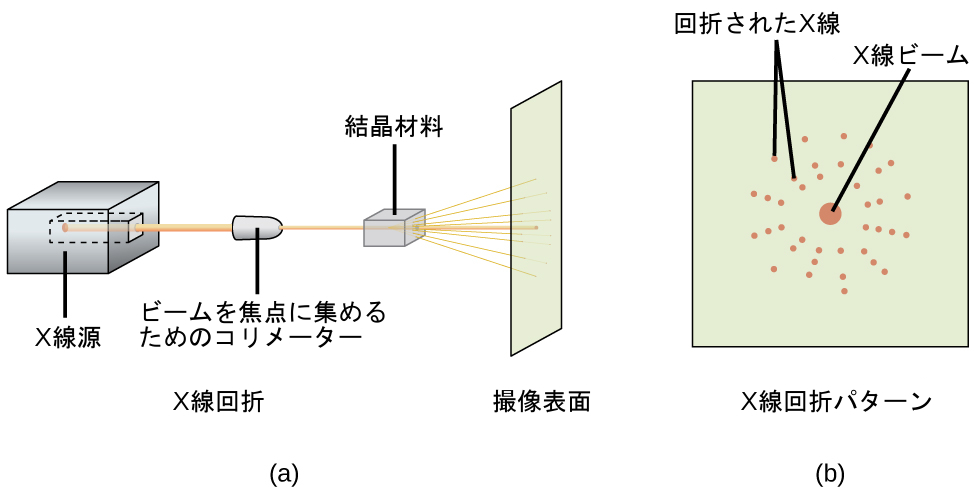
図10.65 | (a)回折計では、X線のビームが結晶材料に当たり、(b)X線回折パターンが得られます。このパターンを分析して結晶構造を決定することができます。
例題10.19 ブラッグ方程式を使用する
回折計で、波長0.1315nmのX線を用いて銅の回折パターンを作成しました。角度θ=25.25°で一次回折(n=1)が発生しました。銅の回折面の間隔を決定してください。
解法
平面の間の距離は、ブラッグ方程式nλ = 2d sinθをdについて解くことによって求められます。これは以下のようになります:
\[ d =\frac{nλ}{\rm 2\ sinθ}=\rm \frac{1(0.1315\ nm)}{2\ sin(25.25°)}= 0.154\ nm \]
学習内容の確認
平面の間の間隔が0.394nmである結晶が、波長0.147nmのX線を回折しました。一次回折の角度は何ですか?
解答:10.8°
化学者の肖像
X線結晶構造解析学者 ロザリンド・フランクリン
1953年にフランシス・クリックとジェームズ・ワトソンがDNAの構造を発見したことは、科学史における偉大な功績の1つです。彼らは、DNAの構造を実験的に証明したモーリス・ウィルキンスとともに、1962年にノーベル医学・生理学賞を受賞しました。イギリスの化学者ロザリンド・フランクリンは、DNAのX線回折像を測定した仕事を通じて、この記念すべき業績に多大な貢献をしました。フランクリンがそのキャリアの初期に行っていた石炭の構造の研究は、イギリスの戦争遂行に役立つことがわかりました。1950年代初頭に生物学的な系に焦点を移した後、フランクリンと博士課程の学生レイモンド・ゴスリングは、DNAには、濡れたときに形成される長く細い繊維(B型)と、乾燥したときに形成される短く幅の広い繊維(A型)の2つの形態があることを発見しました。彼女によるDNAのX線回折像(図10.66)は、DNAが二重らせんを形成していることをワトソンとクリックが確認し、その大きさや構造の詳細を明らかにすることを可能にしてくれるような重要な情報を提供しました。フランクリンはまた、ウイルスとその遺伝情報を含むRNAに関する先駆的な研究も行い、この分野の知識の体系を根本的に変えた新しい情報を発見しました。フランクリンは、卵巣がんを発症した後も、1958年に37歳で亡くなるまで研究を続けました。彼女の業績に対する多くの死後の表彰がなされ、2004年にはフィンチ健康科学大学シカゴ医科大学院はロザリンド・フランクリン医学・科学大学に名称を変更し、彼女の有名なDNAのX線回折画像の図を大学の公式ロゴに採用しました。

図10.66 | この図は、フランクリンが研究の中で発見したものに似たX線回折像を示しています。(credit: National Institutes of Health)
重要用語
接着力:異なる化学的同一性の分子間の引力
非晶質固体(または、非結晶性固体):粒子が秩序のある内部構造を欠いているような固体
体心立方(BCC)固体:角と単位胞の中心に格子点のある、立方体の単位胞を持つ結晶構造
体心立方単位胞:体心立方結晶の最も単純な繰り返し単位。それは、それぞれの角と立方体の中心に格子点を含む立方体である
沸点:液体の蒸気圧がその上にある気体の圧力に等しくなる温度
ブラッグ方程式:X線が結晶内の原子によって回折される角度を関係付ける方程式
毛管現象:液体分子が材料の表面や他の液体分子に引き寄せられることによる多孔質材料内の液体の流れ
クラウジウス-クラペイロン方程式:物質の温度、蒸気圧、蒸発のエンタルピーの間の数学的関係
凝集力:同一分子間の引力
凝縮:気体状態から液体状態への変化
配位数:結晶中の任意の原子に最も近い原子の数、または錯体中の中心金属原子に最も近い原子の数
共有結合ネットワーク性固体:粒子が共有結合によってまとめて保持されている固体
臨界点:そこよりも上では気体が液体に凝縮できないような温度と圧力
結晶性固体:粒子が明確な繰り返しパターンで配置された固体
立方最密充填(CCP):密に充填された原子またはイオンの平面が、異なる相対的な配向の3つの層(ABC)として交互に積層された結晶構造
凝結:気体状態から固体状態への直接の変化
回折:電磁放射が適切な寸法の物理的障壁に遭遇したときに発生する、電磁放射の方向転換
双極子-双極子引力:2つの永久双極子間の分子間引力
分散力(または、ロンドン分散力):2つの急速に変動する一時的な双極子の間の引力。粒子が非常に近くにある場合にのみ重要である
動的平衡:相互の過程が等しい速度で起こる系の状態
面心立方(FCC)固体:角とそれぞれの面の中心に格子点のある、立方体の単位胞からなる結晶構造
面心立方単位胞:面心立方結晶の最も単純な繰り返し単位。それは、それぞれの角とそれぞれの面の中心に格子点を含む立方体である
凍結:液体状態から固体状態への変化
凝固点:物質の固相と液相が平衡にある温度。融点も参照
六方最密充填(HCP):密に充填された原子またはイオンの層が、異なる相対的な配向の2つの層(AB)として交互に積層された結晶構造
正孔(または、間隙):結晶内の原子間の空間
水素結合:非常に強い双極子が引き合うときに発生する。3つの最も電気的に陰性な元素:F、O、またはNのうちの1つに水素が結合したときに存在する結合
誘起双極子:原子や分子の電子が隣接する原子や分子の瞬間的な双極子によって歪められたときに形成される一時的な双極子
瞬間的な双極子:原子や分子の電子が非対称に分布しているときに短い時間だけ起こる一時的な双極子
分子間力:原子、分子、および/またはイオンの間の非共有結合的な引力
格子間サイト:原子またはイオンのあらゆる配列の規則的な粒子の位置の間の空間
イオン性固体: 強い静電引力によってまとめて保持された陽イオンと陰イオンからなる固体
同形:同じ結晶構造を持つ
融解:固体状態から液体状態への変化
融点:物質の固相と液相が平衡にある温度。凝固点も参照
金属性固体:金属原子からなる固体
分子性固体:分子間引力によってまとめて保持された中性分子からなる固体
標準沸点:液体の蒸気圧が1 atm (760 torr)に等しくなる温度
八面体孔:八面体の角に位置する6つの粒子の中心にある結晶内の空きスペース
相図:物質の相が存在することのできる条件をまとめた圧力-温度グラフ
分極率:ある電荷が、分子の電荷分布(電子の雲)をどれだけ歪める能力があるかについての尺度
単純立方構造:角のみに格子点のある、立方体の単位胞を持つ結晶構造
単純立方単位胞(または、基本立方単位胞):単純立方構造の単位胞
空間格子:結晶内の同一環境を持つすべての点
昇華:固体状態から気体状態への直接の変化
超臨界流体:臨界点より上の温度と圧力にある物質。気体状態と液体状態の中間的な性質を示す
表面張力:液体表面の面積(または長さ)を所定の量だけ増加させるのに必要なエネルギー
四面体孔:結晶中の4つの原子またはイオンによって形成される四面体空間
三重点:物質の気相、液相、および固相が平衡にある温度と圧力
単位胞:空間格子の最小部分であり、三次元的に繰り返されて格子全体を形成する
空孔:原子やイオンを含むはずの位置が空になっている場合に発生する欠陥
ファン・デル・ワールス力:分子間の引力または反発力であって、双極子-双極子、双極子-誘起双極子、ロンドン分散力を含む。共有結合またはイオン結合、あるいはイオンと分子の間の引力に起因する力を含まない
蒸気圧(または、平衡蒸気圧):所与の温度で固体または液体と平衡になる蒸気によってかけられる圧力
蒸発:液体状態から気体状態への変化
粘度:液体の流れにくさの尺度
X線結晶構造解析:X線が結晶を通過する際に回折する角度を測定することによって、結晶中の原子間の距離を決定する実験技術
重要な方程式
\(•h =\frac{2T cosθ}{rρg}\)
\(•P = Ae^{−ΔH_{蒸発} /RT}\)
\(•{\rm ln}P = −\frac{ΔH_{蒸発}}{RT}+ {\rm ln} A\)
\(•{\rm ln}\left(\frac{P_2}{P_1}\right)=\frac{ΔH_{蒸発}}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right)\)
\(•nλ= 2d\ {\rm sinθ}\)
この章のまとめ
10.1 分子間力
凝縮した物体(液体と固体)の物理的性質は、分子運動論の観点から説明することができます。液体では、分子間引力が分子を接触したまま保持しますが、それらはまだお互いに移動するのに十分なKEを持っています。
集合的にファン・デル・ワールス力と呼ばれるいくつかの分子間引力は、液体と固体の振る舞いの原因であり、静電的な性質です。双極子-双極子引力は、ある極性分子の部分的に負の端部と別の極性分子の部分的に正の端部との間の静電引力に起因します。原子内の電子の運動に起因する一時的な双極子は、隣接する原子に双極子を誘発し、ロンドン分散力を生じさせることができます。ロンドン力は分子サイズが大きくなるにつれて増加します。水素結合は、3つの最も電気的に陰性な元素:F、O、またはNのうちの1つに水素が結合したときに生じる双極子-双極子引力の特別なタイプです。
10.2 液体の性質
液体状態の分子の間の分子間力は、その化学的同一性に応じて変化し、それに対応したさまざまな物理的性質の変化をもたらします。似た分子間の凝集力は、液体の粘度(流れにくさ)と表面張力(液体表面の弾性)の原因となります。液体の分子とその液体に接触する表面を構成する異なる分子との間の接着力は、表面の濡れや毛管上昇などの現象の原因となります。
10.3 相転移
相転移とは、物質をある物理的状態から別の状態に変換する過程のことです。物質の3つの相の間には6つの相転移があります。融解、蒸発、昇華はすべて吸熱過程であり、分子間の引力を克服するために熱の投入を必要とします。逆の転移である凍結、凝縮、および凝結は、すべて発熱過程であり、分子間の引力が確立または強化されるような熱が関与しています。相転移が発生する温度は、分子間引力の相対的な強さによって決定され、したがって、物質の化学的同一性に依存しています。
10.4 相図
ある物質が固体、液体、気体の状態で存在する温度と圧力の条件は、その物質の相図にまとめられています。相図は、固体-液体、液体-気体、固体-気体という3つの圧力-温度平衡曲線の描画を組み合わせたものです。これらの曲線は、相転移温度と圧力の関係性を表しています。3つの曲線の交点は、その物質の三重点、つまり3つの相がすべて平衡にある温度と圧力を表しています。三重点よりも下の圧力では、温度に関係なく、物質は液体状態で存在することはできません。液体-気体曲線の終点は物質の臨界点、すなわちそこから上は液相が存在できないような圧力と温度を表しています。
10.5 物質の固体状態
一部の物質は、非常に秩序だった構造の粒子からなる結晶性固体を形成します。他の物質は、秩序のない内部構造を持つ非晶質(非結晶性)固体を形成します。結晶性固体の主な種類は、イオン性固体、金属性固体、共有結合ネットワーク性固体、および分子性固体です。異なる種類の結晶性固体の性質は、それらが構成されている粒子の種類、粒子の配置、およびそれらの間の引力の強さに起因しています。結晶性固体の粒子は同一の引力を受けているため、結晶性固体ははっきりとした融解温度を有しています。非晶質固体の粒子は幅のある相互作用を受けているため、非晶質固体は徐々に軟化し、幅を持った温度で融解します。結晶性固体の中には、粒子の明確な繰り返しパターンの中に欠陥を持つものもあります。これらの欠陥(空孔、規則的な位置にない原子やイオン、不純物を含みます)は、電気伝導率などの物理的性質を変化させるものであり、コンピュータチップの製造に使用されるシリコン結晶において利用されています。
10.6 結晶性固体の格子構造
結晶性金属や単純なイオン化合物の構造は、球体の充填の観点から記述することができます。金属原子は、六方最密充填構造、立方最密充填構造、体心構造、および単純立方構造で充填することができます。単純なイオン構造のアニオンは、一般的にこれらの構造のいずれかをとり、カチオンはアニオンの間に残っている空間を占有します。小さなカチオンは、通常、アニオンの最密充填配列の中で四面体孔を占有します。大きなカチオンは、通常、八面体孔を占有します。さらに大きなカチオンは、アニオンの単純立方配列の中で立方体孔を占有することができます。固体の構造は、単位胞の大きさと形状、および単位胞の内容を示すことによって記述することができます。単位胞の構造の種類と寸法は、X線回折測定によって決定することができます。
練習問題
10.1 分子間力
1.そのバルク特性の観点では、液体と固体はどのように異なるでしょうか?また、どのように似ているでしょうか?
2.分子運動論の観点では、液体はどのような点で固体と似ているでしょうか?また、液体はどのような点で固体と異なるでしょうか?
3.分子運動論の観点では、液体はどのような点で気体と似ているでしょうか?また、液体はどのような点で気体と異なるでしょうか?
4.液体は注がれた容器の形をとるのに対し、固体は硬くて自らの形状を保っているのはなぜか説明してください。
5.すべての中性の原子や分子がお互いに引力を及ぼすという証拠は何ですか?
6.PhETの物質の状態シミュレーション(http://openstaxcollege.org/l/16phetvisual)を開いて、以下の質問に答えてください:
(a)固体、液体、気体(Solid, Liquid, Gas)タブを選択してください。さまざまな物質を選択し、系を加熱・冷却したり、状態を変化させたりして調査してみてください。4つの物質のそれぞれの相(固体、液体、気体)の間には、どのような類似点があるか気づきましたか?また、どのような相違点があるか気づきましたか?
(b)それぞれの物質について、それぞれの状態を選択し、与えられた温度を記録してください。それぞれの状態についての与えられた温度は、分子間の引力の強さとどのように相関していますか?説明してください。
(c)相互作用ポテンシャル(Interaction Potential)タブを選択し、既定のネオン原子を使用します。Ne原子を右に動かして、ポテンシャルエネルギーがどのように変化するかを観察してください。合計の力(Total Force)ボタンを選択し、先ほどと同じようにNe原子を動かします。それぞれの原子にかかる合計の力が引き寄せる力であり、影響を及ぼすのに十分なほどの大きさになるのはいつでしょうか?次に、力の成分(Component Forces)ボタンを選択して、Ne原子を動かします。引力(ファン・デル・ワールス力)と反発力(電子の重なり合いの力)は、いつバランスが取れるでしょうか?これは、原子間距離に対するポテンシャルエネルギーのグラフとどのように関係していますか?説明してください。
7.以下のものを定義し、それぞれの例を挙げてください:
(a)分散力
(b)双極子-双極子引力
(c)水素結合
8.物質の分子間力の種類は、それが固体であっても液体であっても気体であっても同じです。では、なぜ物質は気体から液体や固体へと相変化するのでしょうか?
9.なぜ貴ガスの沸点はHe < Ne < Ar < Kr < Xeの順に高くなるのでしょうか?
10.ネオンとHFは分子量がほぼ同じです。
(a)ネオンとHFの沸点が異なる理由を説明してください。
(b)Ne、Ar、Kr、Xeの沸点の変化と、HF、HCl、HBr、HIの沸点の変化を比較し、原子質量または分子量の増加によるそれらの変化の違いを説明してください。
11.以下のそれぞれの化合物の集合を、沸点温度が高くなる順に並べてください:
(a)HCl、H₂O、SiH₄
(b)F₂、Cl₂、Br₂
(c)CH₄、C₂H₆、C₃H₈
(d)O₂、NO、N₂
12.ブタノールC₄H₉OHの分子量は74.14、エチレングリコールCH₂(OH)CH₂OHの分子量は62.08ですが、沸点はそれぞれ 117.2 °C、174 °Cです。この違いの理由を説明してください。
13.分子間引力に基づいて、似たようなモル質量を持つn-ブタン(-1 °C)とクロロエタン(12 °C)の沸点の違いを説明してください。
14.双極子モーメントおよび/または水素結合に基づいて、似たようなモル質量を持つアセトン(56.2°C)と1-プロパノール(97.4°C)の沸点の違いを定性的に説明してください。
15.H₂O(s)の融点は0°Cです。H₂S(s)の融点は-85 °C、0 °C、185 °Cのどれになると予想しますか?あなたの答えを説明してください。
16.シラン(SiH₄)、ホスフィン(PH₃)、硫化水素(H₂S)は、それぞれ-185 °C、-133 °C、-85 °Cで融解します。このことは、3つの化合物の極性と分子間の引力について何を示唆しているでしょうか?
17.2つの水分子間の水素結合が2つのフッ化水素分子間の水素結合よりも弱い理由を説明してください。
18.ある条件下では、酢酸(CH₃COOH)の分子は、「二量体」、すなわち強い分子間引力によってまとめて保持された酢酸分子の対を形成します:
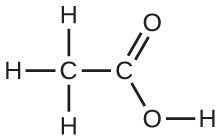
酢酸の二量体を描き、2つのCH₃COOH分子がどのようにまとめて保持されているかを示し、その役割を担うIMFのタイプを述べてください。
19.タンパク質は、さまざまな配置で形成することができるアミノ酸の鎖であり、その配置のうちの1つはらせんです。このような形でタンパク質のストランドを保持しているのは、どのような種類のIMFでしょうか?タンパク質の図上に、タンパク質をまとめて保持しているIMFの位置を示してください:
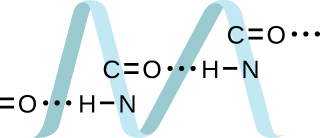
20.液体NH₃の密度は0.64 g/mL、STPでの気体NH₃の密度は0.0007 g/mLです。これらの2つの相の密度の違いを説明してください。
21.以下の固体に存在する分子間力を特定してください:
(a)CH₃CH₂OH
(b)CH₃CH₂CH₃
(c)CH₃CH₂Cl
10.2 液体の性質
22.ここに示されている試験管には、同じ量の特定のモーターオイルが含まれています。同じ金属製の球体をそれぞれの試験管に同時に落下させ、わずかな時間が経った後、球体は図に示される高さまで落下しました。
粘度が高くなる順に順位をつけ、その理由を説明してください:
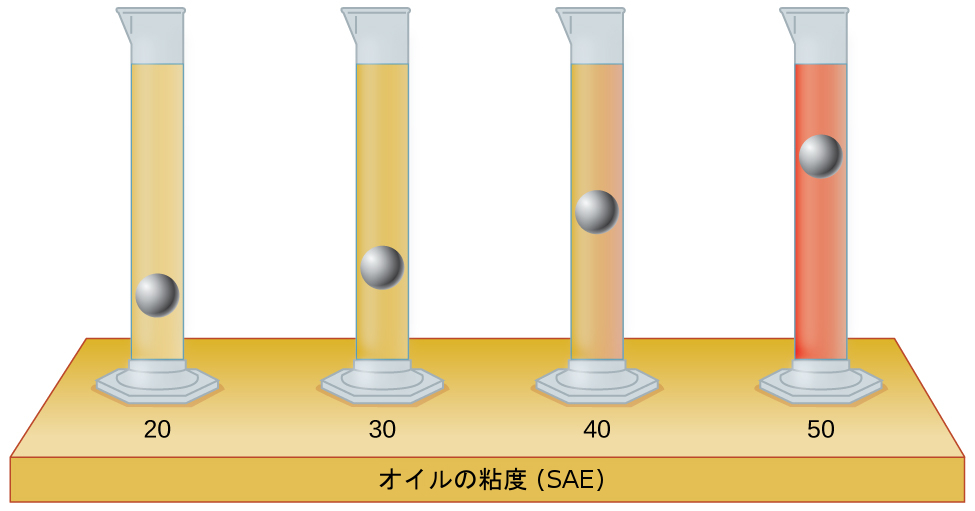
23.スチールは水よりも密度が高いですが、スチールの針やペーパークリップを長さ方向で慎重に静止した水の上に置くことで、それらを水の上に浮かせることができます。これがどのようにして可能になるのか、分子レベルで説明してください。

図10.67 | (credit: Cory Zanker)
24.ジエチルエーテル、アセトン、エタノール、エチレングリコールの表面張力と粘度の値がここに示されています。
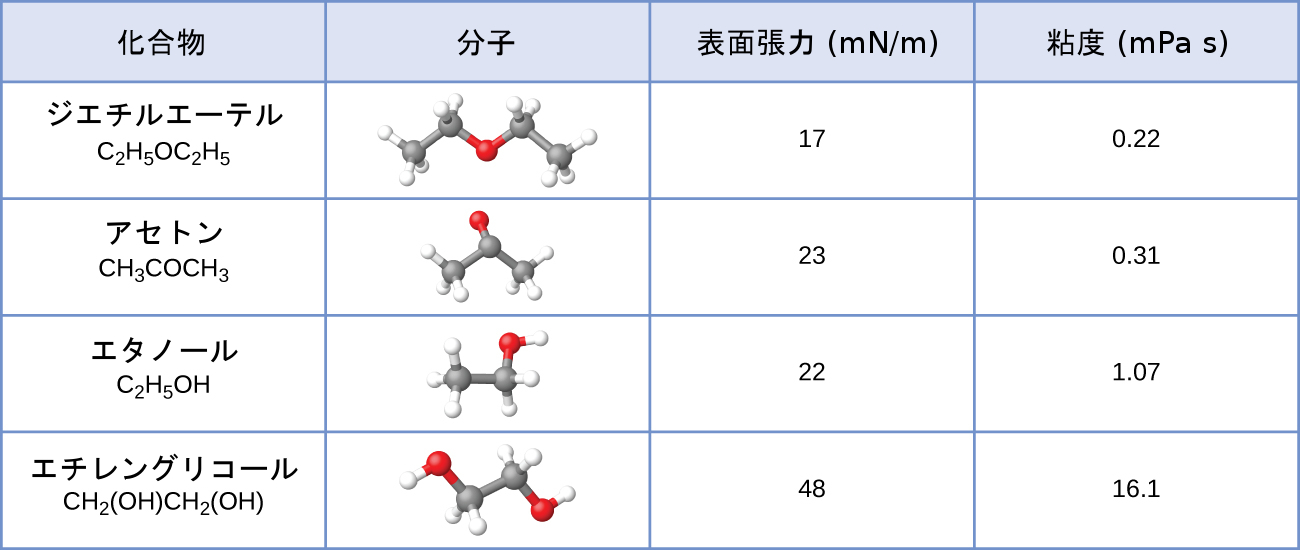
(a)粘度の違いを分子の大きさや形状、およびIMFの観点から説明してください。
(b)表面張力の違いを分子の大きさや形状、およびIMFの観点から説明してください:
25.あなたは、誰かが「冬の糖蜜よりも遅い[遅々として進まないの意味]」という慣用句を使って、ゆっくりと起こるプロセスを表現しているのを聞いたことがあるかもしれません。分子の大きさや形状、分子間の相互作用、および温度変化の影響の概念を用いて、なぜこれが適切な慣用句なのか説明してください。
26.特に冬の寒い日には、運転前に車のエンジンをアイドリング状態にして温めておくことがしばしば推奨されています。長時間のアイドリングの効用は疑わしいですが、暖かいエンジンの方が冷たいエンジンよりも燃費が良いのは確かです。その理由を説明してください。
27.いくつかの異なる温度における水の表面張力と粘度がこの表で与えられています。
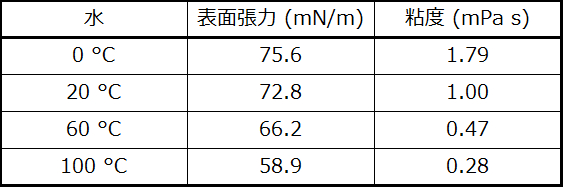
(a)温度が上がるにつれて、水の表面張力には何が起こっていますか?なぜこのようなことが起こるのかを、分子間相互作用と温度変化の影響の観点から説明してください。
(b)温度が上がるにつれて、水の粘度には何が起こっていますか?なぜこのようなことが起こるのかを、分子間相互作用と温度変化の影響の観点から説明してください。
28.25 °Cの場合、内径0.63mmのガラス製の細管の中では水はどれだけの高さに上昇しますか?必要な情報については例題10.4を参照してください。
29.ガラス製の細管の中で水が17cmの高さまで上昇しました。細管の直径は何ですか?
10.3 相転移
30.沸騰したお湯に熱を加えます。沸騰したお湯の温度が変わらない理由を説明してください。変わるものは何ですか?
31.0°Cの氷に熱を加えます。氷の温度が変わらない理由を説明してください。変わるものは何ですか?
32.密閉容器内の液体とその蒸気の間の動的平衡を特徴付けるものは何ですか?
33.いくつかの液体が顕著に蒸発するのに十分な蒸気圧を持っていることを示す2つの一般的な観察を特定してください。
34.ドライアイスや防虫剤のようないくつかの固体が昇華するのに十分な蒸気圧を持っていることを示す2つの一般的な観察を特定してください。
35.液体の中の分子間力とその蒸気圧との間の関係性は何ですか?
36.固体の中の分子間力とその融解温度との間の関係性は何ですか?
37.寒い日よりも暑い日の方がこぼれたガソリンが早く蒸発するのはなぜですか?
38.四塩化炭素(CCl₄)は、かつてドライクリーニング溶剤として使用されていましたが、発がん性があるため、現在では使用されていません。57.8°Cでは、CCl₄の蒸気圧は54.0kPaであり、蒸発のエンタルピーは33.05kJ/molです。この情報を用いて、CCl₄の標準沸点を推定してください。
39.液体の沸点が標準沸点と等しくなるのはいつですか?
40.液体の沸騰は、蒸発とどのように違うでしょうか?
41.図10.24の情報を用いて、大気圧が83.3kPaのときのデンバーにおける水の沸点を推定してください。
42.温度20°Cのシリンジの中に、いかなる蒸気のための空間も存在しないような方法で液体エーテルを入れます。温度を一定に保ち、プランジャーを引き抜いて蒸気が占めることのできる体積を作ると、生成される蒸気のおおよその圧力は何になるでしょうか?
43.以下の観察を説明してください:
(a)テキサス州フォート・デイビス(標高は海面から5000フィート)では、ボストン(海面の高さ)よりも卵を調理するのに時間がかかります。
(b)発汗は体を冷やすためのメカニズムです。
44.水の蒸発のエンタルピーは融解のエンタルピーよりも大きいです。理由を説明してください。
45.以下の物質について、IMFの種類が同じ(分散)であるにもかかわらず、蒸発のモルエンタルピーが、CH₄ < C₂H₆ < C₃H₈の順に増加する理由を説明してください。
46.以下の物質について、3つの物質のモル質量がほぼ同じであるにもかかわらず、蒸発のエンタルピーが、CH₄ < NH₃ < H₂Oの順に増加する理由を説明してください。
47.CO₂(l)の蒸発のエンタルピーは9.8 kJ/molです。CS₂(l)の蒸発のエンタルピーは、28 kJ/mol、9.8 kJ/mol、-8.4 kJ/molのどれになると予想しますか?これらのそれぞれの答えの妥当性について議論してください。
48.フッ化水素分子HFは水分子H₂Oよりも極性が強いです(たとえば、より大きな双極子モーメントを有しています)が、液体フッ化水素の蒸発のモルエンタルピーは水よりも小さいです。説明してください。
49.塩化エチル(沸点13°C)は局所麻酔薬として使用されています。この液体を皮膚に噴霧すると、皮膚を凍らせてしびれるほどに冷却します。液体塩化エチルの冷却効果を説明してください。
50.沸点が高くなる順に正しく記載されている化合物を含むものはどれですか?
(a)N₂ < CS₂ < H₂O < KCl
(b)H₂O < N₂ < CS₂ < KCl
(c)N₂ < KCl < CS₂ < H₂O
(d)CS₂ < N₂ < KCl < H₂O
(e)KCl < H₂O < CS₂ < N₂
51.23.5°Cで422gの液体H₂Oを150°Cの蒸気に変えるのに必要な熱量はどれだけですか?
52.汗の蒸発はエネルギーを必要とするため、余分な熱を体から取り除くことになります。あなたが飲んだ水の一部は、最終的には汗に変換されて蒸発します。3.8°Cの冷蔵庫の中に入っていた20オンスボトルの水をあなたが飲んだ場合、その水をすべて汗に変えて蒸発させるのに必要な熱量はどれだけですか?(注:あなたの体温は36.6°Cです。この問題を解くために、汗の熱的性質が水と同じであると仮定してください。)
53.四塩化チタン(TiCl₄)の融点は-23.2 °Cで、ΔH融解=9.37 kJ/molです。
(a)263.1gのTiCl₄を融解するには、どれだけの量のエネルギーが必要ですか?
(b)TiCl₄の場合、ΔH融解とΔH蒸発のどちらのほうが大きい可能性が高いでしょうか?あなたの推論を説明してください。
10.4 相図
54.水の相図(図10.31)から、以下の条件における水の状態を決定してください:
(a)35 °Cおよび85 kPa
(b)−15 °Cおよび40 kPa
(c)−15 °Cおよび0.1 kPa
(d)75 °Cおよび3 kPa
(e)40 °Cおよび0.1 kPa
(f)60 °Cおよび50 kPa
55.0.005°Cの一定温度で水にさまざまな圧力をかけたとき、どのような相変化が起こるでしょうか?40°Cでは?−40°Cでは?
56.圧力鍋内の圧力が高くなると水の沸騰温度が上がるため、圧力鍋を使うと食品をより早く調理することができます。ある圧力鍋には、圧力が3.4atmを超えると蒸気が抜けるように設定された安全弁が付いています。この圧力鍋の内部で到達できるおおよその最高温度は何ですか?あなたの推論を説明してください。
57.図10.34の二酸化炭素の相図から、以下の条件におけるCO₂の状態を決定してください:
(a)20 °Cおよび1000 kPa
(b)10 °Cおよび2000 kPa
(c)10 °Cおよび100 kPa
(d)−40 °Cおよび500 kPa
(e)−80 °Cおよび1500 kPa
(f)−80 °Cおよび10 kPa
58.(a)-50°Cの一定温度で、(b)50°Cの一定温度で圧力を上げるにつれて、二酸化炭素が起こす相変化を決定してください。温度が-40°Cに保たれている場合ではどうなりますか?20°Cではどうなりますか?(図10.34の相図を参照してください。)
59.初期の圧力65atm、温度20°Cで、気体の二酸化炭素と平衡にある液体の二酸化炭素の混合物が入っているシリンダーを考えてみましょう。一定温度で気体の二酸化炭素が放出されるときのシリンダー圧力の時間変化のプロットを描画してください。
60.CO₂(s)であるドライアイスは大気圧では融解しません。ドライアイスは温度-78°Cで昇華します。CO₂(s)が融解してCO₂(l)を生成する最低圧力は何ですか?これはおおよそどのくらいの温度で起こるでしょうか?(相図は図10.34を参照を参照してください。)
61.もし激しい嵐で停電になった場合には、洗濯物を乾かすために物干し竿を使う必要があるかもしれません。この国の多くの地域の真冬では、洗濯物を物干し竿にかけるとすぐに凍ってしまいます。雪が降っていないのならば、洗濯物はなんとか乾くでしょうか?あなたの答えを説明してください。
62.室温(約25°C)で窒素を液化することは可能ですか?室温で二酸化硫黄を液化することは可能ですか?あなたの答えを説明してください。
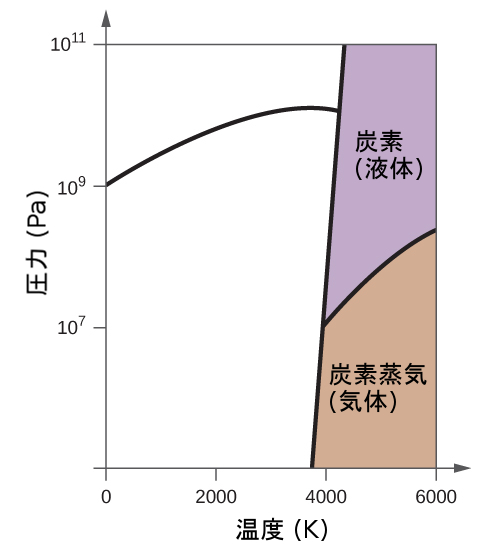
63.元素の炭素は、この相図に示されるように、1つの気相、1つの液相、2つの異なる固相を有しています:
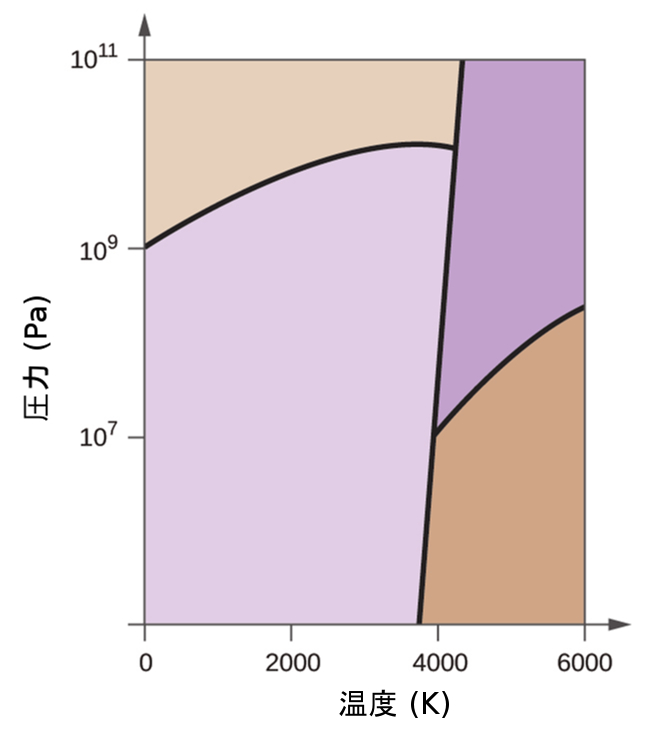
(a)この相図上で、気相と液相の領域に表示を付けてください。
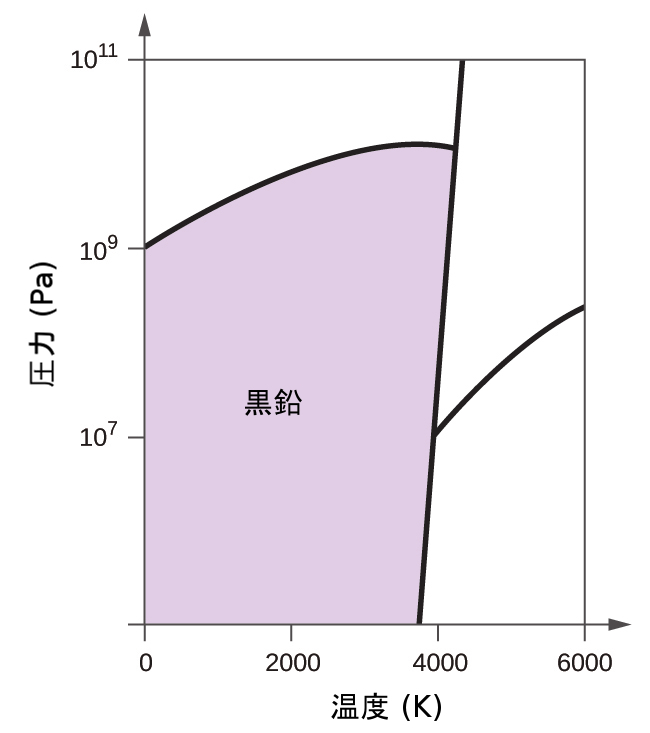
(b)黒鉛は、通常の条件では炭素の中で最も安定な相です。この相図上で黒鉛相に表示を付けてください。
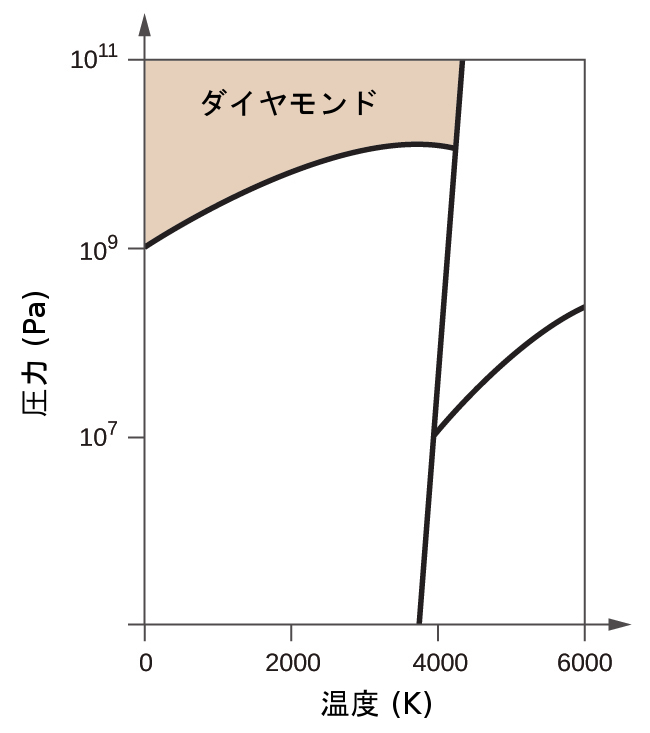
(c)もし通常の条件の黒鉛を2500Kに加熱し、圧力を10¹⁰Paに上げると、それはダイヤモンドに変化します。ダイヤモンド相に表示を付けてください。
(d)相図のそれぞれの三重点を丸で囲んでください。
(e)炭素は、5000 K、10⁸Pa のとき、どのような相に存在していますか?
(f)10⁶Paの一定圧力で炭素の試料の温度が3000Kから5000Kまで上昇した場合、(もし起こるならば)どの相転移が起こりますか?
10.5 物質の固体状態
64.どのような種類の液体が通常は非晶質固体を形成しますか?
65.非常に低温では、酸素(O₂)は凍結して結晶性固体を形成します。これらの結晶を最もよく表しているのはどれですか?
(a)イオン性
(b)共有結合ネットワーク性
(c)金属性
(d)非晶質
(e)分子性結晶
66.オリーブオイルは、冷やしていくとゆっくりと固まり、範囲を持った温度で固体を形成します。この固体を最もよく表しているのはどれですか?
(a)イオン性
(b)共有結合ネットワーク性
(c)金属性
(d)非晶質
(e)分子性結晶
67.結晶性固体である氷は融解温度が0°Cであるのに対し、非晶質固体であるバターは範囲を持った温度で柔らかくなる理由を説明してください。
68.以下のそれぞれの物質によって形成される結晶性固体の種類(金属性、共有結合ネットワーク性、イオン性、分子性)を特定してください:
(a)SiO₂
(b)KCl
(c)Cu
(d)CO₂
(e)C (ダイヤモンド)
(f)BaSO₄
(g)NH₃
(h)NH₄F
(i)C₂H₅OH
69.以下のそれぞれの物質によって形成される結晶性固体の種類(金属性、共有結合ネットワーク性、イオン性、分子性)を特定してください:
(a)CaCl₂
(b)SiC
(c)N₂
(d)Fe
(e)C (黒鉛)
(f)CH₃CH₂CH₂CH₃
(g)HCl
(h)NH₄NO₃
(i)K₃PO₄
70.表中のそれぞれの物質を金属性固体、イオン性固体、分子性固体、共有結合ネットワーク性固体のいずれかに分類してください:

71.表中のそれぞれの物質を金属性固体、イオン性固体、分子性固体、共有結合ネットワーク性固体のいずれかに分類してください:

72.以下の物質をイオン性固体、金属性固体、共有結合ネットワーク性固体、または分子性固体として特定してください:
物質Aは展性と延性があり、電気をよく通し、融点は1135°Cです。物質Bは脆く、固体としては電気を通さないが、溶融すると電気を通し、融点は2072°Cです。物質Cは非常に硬く、電気を通さず、融点は3440 °Cです。物質Dは柔らかく、電気を通さず、融点は185°Cです。
73.物質Aは光沢があり、電気をよく通し、975°Cで融解します。物質Aは以下のどれの可能性が高いですか:
(a)イオン性固体
(b)金属性固体
(c)分子性固体
(d)共有結合ネットワーク性固体
74.物質Bは硬く、電気を通さず、1200°Cで融解します。物質Bは以下のどれの可能性が高いですか:
(a)イオン性固体
(b)金属性固体
(c)分子性固体
(d)共有結合ネットワーク性固体
10.6 結晶性固体の格子構造
75.立方体の単位胞内に2個分の金属原子を持って結晶化する鉄の結晶構造を記述してください。
76.立方体の単位胞内に4個分の金属原子を持って結晶化するPtの結晶構造を記述してください。
77.クロムの体心立方構造におけるクロム原子の配位数は何ですか?
78.アルミニウムの面心立方構造におけるアルミニウム原子の配位数は何ですか?
79.コバルト金属は六方最密充填構造で結晶化します。コバルト原子の配位数は何ですか?
80.ニッケル金属は立方最密充填構造で結晶化します。ニッケル原子の配位数は何ですか?
81.タングステンは、辺の長さが3.165Åの体心立方単位胞で結晶化します。
(a)この構造のタングステンの原子半径は何ですか?
(b)タングステンの密度を計算してください。
82.白金(原子半径1.38Å)は立方体の密に充填された構造で結晶化します。面心立方単位胞の辺の長さと白金の密度を計算してください。
83.バリウムは、辺の長さが5.025Åの体心立方単位胞で結晶化します。
(a)この構造のバリウムの原子半径は何ですか?
(b)バリウムの密度を計算してください。
84.アルミニウム(原子半径=1.43Å)は立方体の密に充填された構造で結晶化します。面心立方単位胞の辺の長さとアルミニウムの密度を計算してください。
85.アルミニウムの密度は2.7g/cm³、ケイ素の密度は2.3g/cm³です。Siの方が重い原子を持っているにもかかわらず、密度が低いのはなぜかを説明してください。
86.金属の中の空いた空間は、単位胞の体積から単位胞内の原子の体積を引くことによって求めることができます。すべての原子が同じ大きさで、最も近い隣接原子に接している場合、3つの立方格子のそれぞれの中の空いた空間の割合を計算してください。これらの構造のうち、最も効率的な充填を表しているのはどれですか?つまり、未使用の空間の量が最も少なくなるように充填されているものはどれですか?
87.芸術家が黄色の顔料として使用することもある硫化カドミウムは、硫化物イオンが最密充填配列で、カドミウムが四面体孔の2分の1を占めるように結晶化します。硫化カドミウムの化学式は何ですか?あなたの答えを説明してください。
88.カドミウム、スズ、およびリンの化合物は、一部の半導体の製造に使用されています。それは、リン化物イオンが最密充填配列で、カドミウムが四面体孔の4分の1を占め、スズが四面体孔の4分の1を占めるように結晶化します。この化合物の化学式は何ですか?あなたの答えを説明してください。
89.記録テープに使われるコバルトの磁性酸化物は、酸化物イオンが密に充填された配列で、コバルト原子が四面体孔の8分の1と八面体孔の2分の1を占めるように結晶化します。この化合物の化学式は何ですか?
90.亜鉛、アルミニウム、および硫黄を含む化合物は、硫化物イオンの最密充填配列で結晶化します。亜鉛イオンは四面体孔の8分の1に、アルミニウムイオンは八面体孔の2分の1に存在します。この化合物の経験式は何ですか?
91.タリウムとヨウ素の化合物は、ヨウ化物イオンが単純立方配列で、タリウムイオンが立方体孔のすべてに存在するように結晶化します。このヨウ化物の化学式は何ですか?あなたの答えを説明してください。
92.以下の元素のうち、硫黄と反応して、硫黄原子が最密充填配列を形成するとともに元素が八面体孔のすべてを占有するように固体を形成するものはどれですか:Li、Na、Be、Ca、またはAl?
93.チタンと酸素を含む鉱物であるルチルを、もし酸化物イオンが最密充填配列でチタンイオンが八面体孔の2分の1に含まれる構造として記述することができるならば、ルチル中のチタンの質量%は何になりますか?チタンの酸化数はいくつですか?
94.化学的に似たアルカリ金属の塩化物であるNaClとCsClは構造が異なるのに対し、化学的に異なるNaClとMnSは構造が同じであるのはなぜかを説明してください。
95.溶融したマグマから鉱物が形成されるにつれて、その結晶中で異なるイオンが同じサイトを占めました。リチウムは、イオンの電荷の違いにもかかわらず、鉱物の中でマグネシウムと一緒に現れることがしばしばあります。説明を提案してください。
96.ヨウ化ルビジウムは、角にヨウ化物イオン、中央にルビジウムイオンを含む立方体の単位胞で結晶化します。この化合物の化学式は何ですか?
97.さまざまなマンガン酸化物のうちの1つは、角と中心にマンガンイオンを含む立方体の単位胞で結晶化します。酸化物イオンは、単位胞のそれぞれの辺の中央に位置しています。この化合物の化学式は何ですか?
98.NaHはNaClと同じ結晶構造で結晶化します。NaHの立方体の単位胞の辺の長さは4.880Åです。
(a)H⁻のイオン半径を計算してください。(Li⁺のイオン半径は0.95Åです。)
(b)NaHの密度を計算してください。
99.ヨウ化タリウム(I)はCsClと同じ構造で結晶化します。TlIの単位胞の辺の長さは4.20Åです。Tl⁺のイオン半径を計算してください。(I⁻のイオン半径は2.16Åです。)
100.ある立方体の単位胞の角にはマンガンイオンが、それぞれの辺の中心にはフッ化物イオンが含まれています。
(a)この化合物の経験式は何ですか?あなたの答えを説明してください。
(b)Mn³⁺イオンの配位数は何ですか?
(c)Mn³⁺イオンの半径が0.65 Aである場合の、単位胞の辺の長さを計算してください。
(d)この化合物の密度を計算してください。
101.波長1.541nmのX線を15.55°の角度θで回折(一次反射)する結晶面の間隔は何ですか?
102.波長0.2287nmのX線を用いた回折計が、結晶角度θ=16.21°で一次回折ピークを生じました。この結晶の回折面の間の間隔を決定してください。
103.平面間の間隔が0.4164 nmである金属が、波長0.2879 nmのX線を回折します。一次回折ピークの回折角度は何ですか?
104.金は面心立方単位胞で結晶化します。単位胞の上面と下面を構成する面によるX線の2次反射(n=2)は、θ=22.20°で生じます。X線の波長は1.54Åです。金属の金の密度は何ですか?
105.励起されたモリブデン原子の電子がL殻からK殻に落ちるとX線が放出されます。これらのX線は2.64Åの間隔で離れた平面によって7.75°の角度で回折されます。 一次回折を仮定した場合、モリブデンのK殻とL殻の間のエネルギーの差は何ですか?
解答のヒント
1.液体と固体は、原子、イオン、または分子からなる物質であるという点で似ています。それらは、非圧縮性であり、似たような密度を有しています。どちらの密度も、気体の密度よりもはるかに大きいです。液体は固定された形状を持たず、固体は硬直しているという点で、液体と固体は異なっています。
3.それらは、原子や分子がある位置から別の位置に自由に移動できるという点で似ています。液体の粒子は入れられた容器の形に限定されていますが、対照的に、気体は置かれた空間を満たすために制限なく拡張していくという点でそれらは異なります。
5.すべての原子や分子は、十分に低い温度では、引力が分子の運動エネルギーを上回る液体や固体へと凝縮します。
7.(a)ある原子における電子が原子核の周りに非対称的に分布しているときに、その原子で一時的な双極子モーメントが生じることで分散力が発生します。この構造は、アルゴンやラドンのような大きな原子により多く見られます。第二の原子は、第一の原子における双極子の出現により歪められます。第二の原子の電子は第一の原子の正の端部に引き寄せられ、それにより第二の原子に双極子が生じます。正味の結果として、急速に変動する一時的な双極子がお互いに引き寄せ合うことになります(例:Ar)。(b)双極子-双極子引力とは、ある極性分子の正の端部が別の極性分子の負の端部に対して静電的に引力を持つことから生じる力です(たとえば、ICl分子は双極子-双極子相互作用によって互いに引き寄せ合います)。(c)水素結合は、水素原子が、フッ素原子、酸素原子、または窒素原子などのより電気的に陰性な原子のうちの1つに結合している場合にはいつでも形成されます。ある分子の部分的に正の水素原子と別の分子の部分的に負の原子との間の静電引力は、水素結合と呼ばれる強い双極子-双極子相互作用を生じさせます(例: HF…HF)。
9.ロンドン力は通常、電子の数が増えるにつれて増加します。
11.(a)SiH₄ < HCl < H₂O、(b)F₂ < Cl₂ < Br₂、(c)CH₄ < C₂H₆ < C₃H₈、(d)N₂ < O₂ < NO
13.C-H結合からのかなり小さな双極子-双極子相互作用だけが液体状態のn-ブタンを保持するために利用されています。しかしながら、クロロエタンはCl-C結合のために双極子相互作用がかなり大きく、したがって相互作用が強くなり、沸点が高くなります。
15.−85 °C。水は強い水素結合を有するので、より高い温度で融解します。
17.2つのフッ化水素分子間の水素結合は、2つの水分子間の水素結合よりも強いです。なぜなら、Fの電気陰性度がOの電気陰性度よりも大きいからです。その結果、Fにある部分的に負の電荷はOにある部分的に負の電荷よりも大きくなります。部分的に正のHとより大きな部分的に負のFとの間の水素結合は、HとOとの間に形成される水素結合よりも強くなります。
19.H結合は、タンパク質のストランドをまとめて保持する主要なIMFです。H結合は、N-HとC=Oの間にあります。
21.(a)水素結合、双極子-双極子引力、分散力、(b)分散力、(c)双極子-双極子引力と分散力
23.水分子は水素結合という強い分子間力を持っています。したがって、水分子は互いに強く引きつけ合い、比較的大きな表面張力を示し、その表面に一種の「皮」を形成しています。この皮は、水の上にそっと置かれた虫や紙クリップを支えることができます。
25.温度は分子間力に影響を与えます:温度が高いほど、分子の運動エネルギーが大きく、克服することのできる分子間力の範囲が大きくなるため、液体が流動的になります(粘度が低いです)。温度が低いほど克服することのできる分子間力が小さいので、粘度の低い液体になります。
27.(a)水が高温になると、分子の運動エネルギーの増加が水素結合を克服するのにより有効となるため、表面張力が低下します。表面張力と分子間力は直接関係があります。(b)粘度と同じ傾向が表面張力でも見られます。これも同じ理由です。
29.1.7 × 10⁻⁴m
31.熱は氷に吸収され、固体の分子間の引力を部分的に克服するために必要なエネルギーを提供し、液体の水への相転移を引き起こします。溶液は、すべての氷が溶けるまで0°Cのままです。氷がなくなるまでは、氷として存在する水の量だけが変化します。その後、水の温度は上昇することができるようになります。
33.私たちは、開いた容器の中の液体の量が減っていくのを見ることができるとともに、いくつかの液体の蒸気の匂いを嗅ぐことができます。
35.液体の蒸気圧は、分子間力の強さが増すと低下します。
37.温度が高くなると、ガソリンの分子の平均運動エネルギーが増加するので、低温時よりも多くの割合の分子が液体から脱出するのに十分なエネルギーを持つことになります。
39.液体の上にある気体の圧力がちょうど1atmのとき、それらは等しくなります。
41.約95 °C
43.(a)標高5000フィートでは、海面よりも気圧が低いため、水はより低い温度で沸騰します。この低い温度のために、卵の調理に関わる物理的・化学的変化がよりゆっくりと進行し、卵を完全に調理するにはより長い時間が必要となります。(b)身体を取り囲む空気が、その温度で空気が保持できる最大量よりも少ない水蒸気を含んでいる限り、汗が蒸発し、それによって水を蒸発させるのに必要な蒸発熱が除去されて身体が冷却されます。
45.分散力は分子量や分子の大きさによって大きくなります。この同族列の分子を構成する原子の数が増えると、分散力を介した分子間引力の程度が大きくなり、その結果、これらの力を克服して液体を蒸発させるのに必要なエネルギーも大きくなります。
47.CS₂の沸点は、CO₂の沸点よりも高いです。それは、部分的にはCS₂の分子の重さが大きいからです。その結果、引力はCS₂のほうがより強いです。したがって、蒸発熱はCO₂の9.8 kJ/molよりも大きくなるだろうと予想されます。28 kJ/mol が妥当に見えるでしょう。−8.4 kJ/molという値は、蒸発時にエネルギーが放出されることを示してしまいますが、これは明らかにあり得ないことです。
49.液体を蒸発させるのに必要な熱エネルギー(熱)が皮膚から取り除かれます。
51.1130 kJ
53.(a)13.0kJ。(b)蒸発の場合は分子間相互作用を完全に克服しなければならないのに対し、融解の場合は分子間相互作用の一部だけを弱めたり破壊したりするので、蒸発熱の方がより大きな程度を有する可能性が高いです。
55.低い圧力と0.005°Cでは、水は気体です。圧力が4.6torrまで上昇すると、水は固体になり、圧力がさらに上昇すると液体になります。40°Cでは、低圧の水は蒸気ですが、約75torrより大きな圧力になると液体に変化します。−40°Cでは、圧力が非常に低い値を超えるように上昇すると、水は気体から固体になります。
57.(a)気体、(b)気体、(c)気体、(d)気体、(e)固体、(f)気体
59.
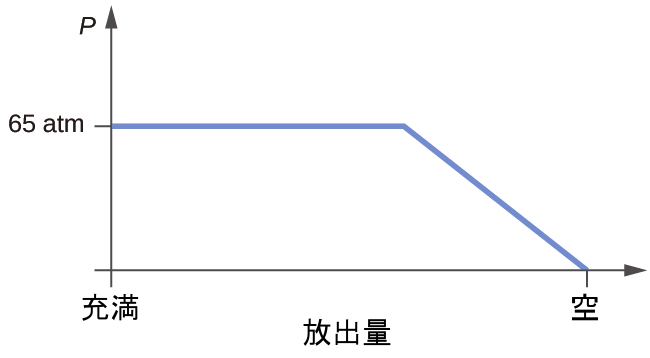
61.はい、氷は昇華します(ただし、数日かかるかもしれませんが)。氷は蒸気圧が小さく、一部の氷の分子が気体を形成して氷の結晶から脱出します。時間が経つにつれ、より多くの固体が気体に変換され、最終的に衣類が乾きます。
63.(a)
(b)
(c)
(d)
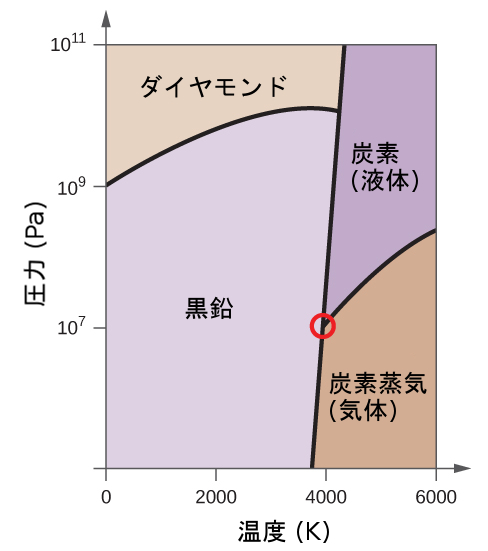
(e)液相(f)昇華
65.(e)分子性結晶
67.氷は水素結合によって安定化された結晶構造を有しています。これらの分子間力は同等の強さであるため、克服するには同じ量のエネルギーを必要とします。その結果、氷は単一の温度で融解するのであって、範囲を持った温度範囲で融解することはありません。バターを構成するさまざまな種類の非常に大きな分子は、さまざまな温度で克服されるようなさまざまな強さのさまざまなファン・デル・ワールス引力を経験するので、融解プロセスは広い温度範囲にわたって発生します。
69.(a)イオン性、(b)共有結合ネットワーク性、(c)分子性、(d)金属性、(e)共有結合ネットワーク性、(f)分子性、(g)分子性、(h)イオン性、(i)イオン性
71.X = イオン性、Y = 金属性、Z = 共有結合ネットワーク性
73.(b)金属性固体
75.鉄のこの低温形態(910°C未満)の構造は、体心立方構造です。立方体の8つの角のそれぞれに8分の1の原子があり、立方体の中心には1つの原子があります。
77.8
79.12
81.(a)1.370 Å、(b)19.26 g/cm³
83.(a)2.176 Å、(b)3.595 g/cm³
85.Siの結晶構造は、Al(配位数12)に比べるとSiが固体中で密に詰め込まれていない(配位数4)ことを示しています。
87.最密充填配列では、それぞれのアニオンに対して2つの四面体孔が存在します。四面体孔の半分だけが占有されている場合、アニオンとカチオンの数は等しいです。硫化カドミウムの化学式はCdSです。
89.Co₃O₄
91.単純立方配列では、配列内のそれぞれのアニオンについて、1つの立方体孔だけがカチオンにより占有されます。タリウムとヨウ素の比率は1:1でなければなりません。したがって、タリウムの化学式はTlIです。
93.59.95%。チタンの酸化数は+4です。
95.両方のイオンの大きさは似ています:Mgは0.65で、Liは0.60です。この類似性により、両者はかなり容易に入れ替わることができます。電荷の違いは、一般的にSi⁴⁺をAl³⁺に置き換えることで補われます。
97.Mn₂O₃
99.1.48 Å
101.2.874 Å
103.20.2°
105.1.74 × 10⁴eV
この訳文は元の本のCreative Commons BY 4.0ライセンスに従って同ライセンスにて公開します。問題がありましたら、可能な限り早く対応いたしますので、ご連絡ください。また、誤訳・不適切な表現等ありましたらご指摘ください。この本は、https://openstax.org/details/books/chemistry-2eで無料でダウンロードできます。