第5章 熱化学

図5.1 | マッチの頭を粗い表面に沿って滑らせると、燃焼反応が始まり、熱と光の形態でエネルギーが発生します。(credit: modification of work by Laszlo Ilyes)
この章の概要
5.1 エネルギーの基本
5.2 熱量測定
5.3 エンタルピー
はじめに
あなたがマッチに火をつけたときに起こるもののような化学反応は、物質だけでなくエネルギーの変化も伴います。発展のいかなるレベルにある社会であっても、化学反応によって放出されるエネルギーがなければ機能できないでしょう。2012年のアメリカのエネルギー消費量の約85%は、石油製品、石炭、木材、ゴミの燃焼によるものでした。私たちはこのエネルギーを、電気の発生(38%)、食品、原材料、製造物、および人の輸送(27%)、工業生産(21%)、私たちの家庭や事業所の暖房や電力供給(10%)に使用しています[1]。これらの燃焼反応は、私たちの必須のエネルギー需要を満たすのに役立つ一方で、それらは地球規模の気候変動に対する主要な要因であると、科学界の大多数の人々によって認識されています。
有用な形態のエネルギーは、燃焼以外のさまざまな化学反応からも得られます。たとえば、携帯電話や自動車、懐中電灯などの中にある電池が生み出すエネルギーは、化学反応の結果です。この章では、熱エネルギーへと焦点を合わせ、化学的変化とエネルギーとの間の関係性を探るために必要な基本的な考え方の多くを紹介します。
5.1 エネルギーの基本
この節が終わるまでに、あなたは次のことができるようになります:
•エネルギーを定義し、エネルギーの種類を区別し、化学的および物理的変化に伴うエネルギーの変化の性質を記述する
•熱、熱エネルギー、温度という、関連する性質を区別する
•比熱と熱容量を定義して区別するとともに、両者の物理的な意味合いを記述する
•熱、比熱、温度変化が関係する計算を行う
化学的変化とそれに伴うエネルギーの変化は、私たちの日常的な世界の重要な部分を占めています(図5.2)。食べ物に含まれる主要栄養素(タンパク質、脂肪、炭水化物)は代謝反応を経て、私たちの体の機能を維持するためのエネルギーを供給しています。私たちはさまざまな燃料(ガソリン、天然ガス、石炭)を燃やして、輸送、暖房、発電などのエネルギーを作り出しています。工業的な化学反応では、原材料(鉄やアルミニウムなど)を生産するために膨大なエネルギーが使われます。そして、これらの原材料を自動車や高層ビル、橋などの有用な製造物へと作り上げるためにエネルギーが使われています。

図5.2 | 化学的変化に伴うエネルギーは、私たちの日常生活にとって重要なものです:(a)昼食のチーズバーガーは、あなたが1日の残りの時間を過ごすために必要なエネルギーを与えてくれます。(b)ガソリンの燃焼は、あなたの車(とあなた)が家、職場、学校の間を移動するためのエネルギーを供給します。(c)石炭の加工形態であるコークスは、鉄鉱石を鉄に変換するために必要なエネルギーを供給しています。鉄は、私たちが日常的に使用する多くの製品を作るために不可欠なものです。(credit a: modification of work by “Pink Sherbet Photography”/Flickr; credit b: modification of work by Jeffery Turner)
私たちが使用しているエネルギーの90%以上は、もともと太陽からもたらされたものです。太陽は毎日、その日の世界のエネルギー需要のすべてを満たすために必要な量の約1万倍ものエネルギーを地球に供給しています。私たちの課題は、やって来る太陽エネルギーを変換して貯蔵し、便利で汚染のない反応や化学プロセスに利用できるようにする方法を見つけることです。植物や多くの細菌は、光合成を通じて太陽エネルギーを捕まえます。私たちは、木材やエタノールなどの植物製品を燃やすときに、植物に蓄えられたエネルギーを放出します。また、私たちは、直接採取した植物や、植物を食べてエネルギーを得た動物からなる食物を食べることにより、このエネルギーを私たちの体の燃料として利用しています。石炭や石油を燃やすこともまた、蓄えられた太陽エネルギーを放出するものです:これらの燃料は、化石化した植物や動物です。
この章では、化学的および物理的変化の際に吸収されたり放出されたりする熱の量に関係する科学の重要な分野、すなわち熱化学と呼ばれる分野の基本的な考え方を紹介します。この章で紹介する概念は、ほとんどすべての科学・技術分野で広く使われています。食品科学者は、食品のエネルギー含有量を決定するためにそれらの概念を使用しています。生物学者は、糖が二酸化炭素と水へと代謝的に燃焼することなどの、生物のエネルギー論を研究しています。石油・ガス・輸送業界、再生可能エネルギー供給業者、その他多くの企業は、私たちの商業的および個人的な必要性に対してエネルギーを生産するためのより良い方法を見つけることを試みています。エンジニアは、エネルギー効率を改善すること、すなわち、私たちの家屋を暖房や冷房したり、食品や飲料を冷蔵したり、コンピュータや電子機器におけるエネルギーや冷却のニーズを満たしたり、その他多くの用途のためのより良い方法を見つけることのために努力しています。熱化学の原理を理解することは、化学者、物理学者、生物学者、地質学者、あらゆる種類のエンジニア、そしてあらゆる種類の科学を研究している、あるいは行っているどのような人にとっても必要不可欠なことです。
エネルギー
エネルギーは、熱を供給したり、仕事をしたりする能力として定義することができます。仕事(w)の1つのタイプは、物質を反対の力に逆らって動かすようにするプロセスです。たとえば、私たちは自転車のタイヤに空気を入れるときに仕事をしていますが、このとき私たちは、すでにタイヤの中に入っている空気による反対の力に逆らって物質(ポンプの中の空気)を動かしています。
物質と同じように、エネルギーにもさまざまな種類があります。ある方式では、エネルギーを2つの種類に分類しています:それは、物体の相対的な位置、組成、または状態によって物体が持つエネルギーであるポテンシャルエネルギーと、物体が運動によって持つエネルギーである運動エネルギーです。滝やダムの上部にある水は、その位置によってポテンシャルエネルギーを持ちます。その水が発電機を通過して下に流れるときには、水は運動エネルギーを持っており、その運動エネルギーは仕事をしたり水力発電所で発電したりするために使われます(図5.3)。電池は、電池の中にある化学物質が、仕事をすることのできるような電気を作り出すことができるため、ポテンシャルエネルギーを持っています。

図5.3 | (a)ビクトリアの滝の上部など、高いところにある水は、低いところにある水よりも大きなポテンシャルエネルギーを持っています。水が落ちると、そのポテンシャルエネルギーの一部が運動エネルギーに変換されます。(b)ここに示されるフーバーダムのように、ダムの下部にある発電機を通過するように水が流れると、その運動エネルギーは電気エネルギーに変換されます。(credit a: modification of work by Steve Jurvetson; credit b: modification of work by “curimedia”/Wikimedia commons)
エネルギーはある形態から別の形態に変換することができますが、変化が起こる前に存在していたエネルギーのすべては、変化が完了した後も常に何らかの形態で存在しています。この観察は、エネルギーの保存の法則で表現されます:化学的または物理的な変化の間、エネルギーは形態を変えることができますが、作られたり破壊されたりすることはできません。(これは、あなたが後に学ぶ熱力学の第一法則の1つのバージョンでもあります。)
ある物質が別の物質に変換されるとき、関連したエネルギーのある形態から別の形態への変換が常に存在しています。熱は通常、放出されたり吸収されたりしますが、時には光や電気エネルギー、あるいは他の何らかのエネルギーの形態に変換されることもあります。たとえば、ガソリンを構成する分子には、化学エネルギー(ポテンシャルエネルギーの一種)が貯蔵されています。自動車のエンジンのシリンダー内でガソリンを燃焼させると、この化学反応による気体状の生成物が急激に膨張し、シリンダーのピストンを動かして機械的エネルギー(運動エネルギーの一種)を発生させます。
以前の章で見た物質の保存の法則によれば、化学的変化の間には物質の総量には検出可能な変化はありません。化学反応が起こるときには、エネルギーの変化は比較的小さく、質量の変化は測定できないほど小さいので、物質とエネルギーの保存の法則がよく成り立ちます。しかしながら、核反応では、エネルギーの変化ははるかに大きく(百万倍といった程度)、質量の変化は測定可能であり、物質-エネルギー変換が顕著になります。このことについては、後の核化学の章でより詳しく調べます。
熱エネルギー・温度・熱
熱エネルギーは、原子や分子のランダムな運動に関連する運動エネルギーです。温度は「熱い」か「冷たい」かについての定量的な尺度です。物体の中の原子や分子が速く動いたり振動したりしているときは、それらの平均運動エネルギー(KE)は高く、私たちはその物体が「熱い」と言います。原子や分子がゆっくり動いているときは、それらの平均運動エネルギーは低く、私たちはその物体が「冷たい」と言います(図5.4)。化学反応や相変化(融解や蒸発など)が起こらないと仮定すると、物質の試料の中の熱エネルギー量が増大すれば、その温度が上昇します。また、化学反応や相変化(凝縮や凝固など)が起こらないと仮定すると、物質の試料の中の熱エネルギー量が減少すれば、その温度が低下します。
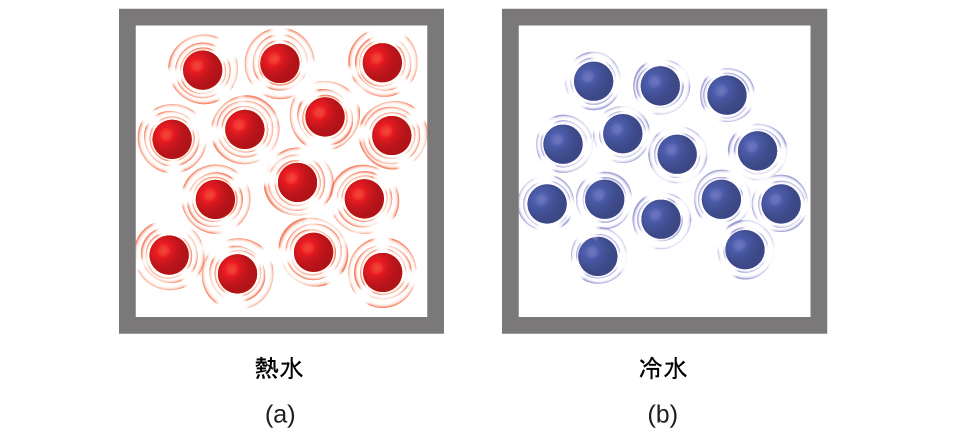
図5.4 | (a)熱水の試料の中の分子は、(b)冷水の試料の中の分子よりも速く動いています。
学習へのリンク
このインタラクティブシミュレーション(http://openstaxcollege.org/l/16PHETtempFX)をクリックして、温度が分子運動に与える影響を見てください。
ほとんどの物質は温度が上がると膨張し、温度が下がると収縮します。この性質を利用して、図5.5に示されるように、温度変化を測定することができます。多くの温度計の動作は、温度変化に対する物質の膨張・収縮に依存しています。
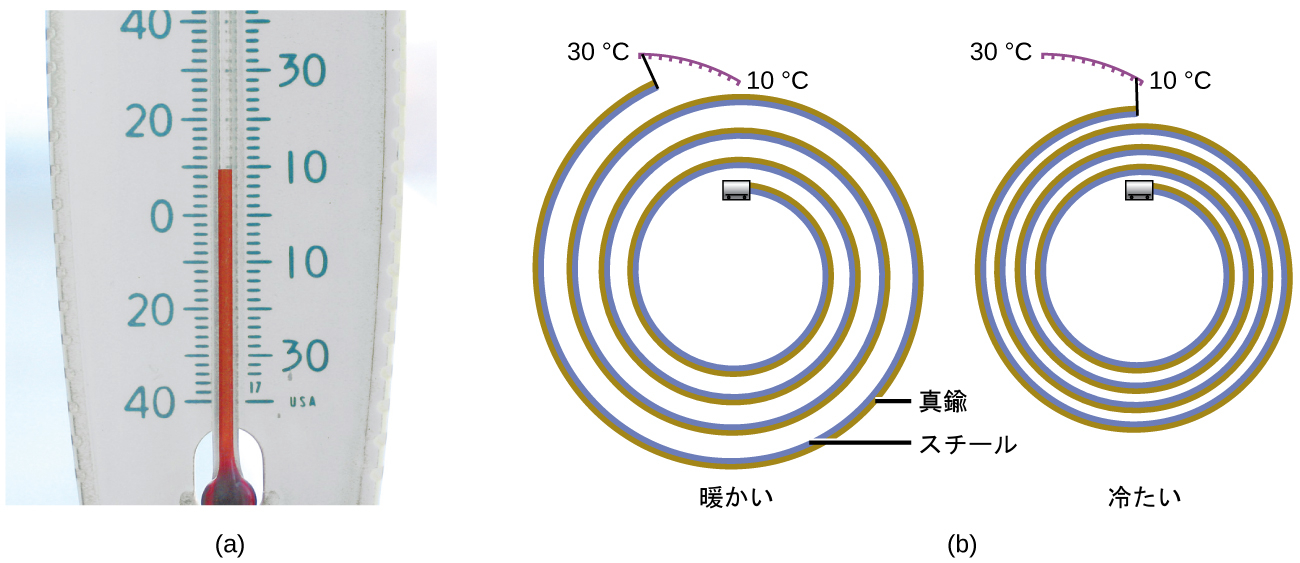
図5.5 | (a)アルコールや水銀の温度計では、加熱されると液体(視認性のために赤く染められています)が膨張し、冷却されると収縮しますが、これは液体が収容されているガラス管よりもはるかに大きなものです。(b)バイメタル温度計では、2つの異なる金属(真鍮とスチールなど)が2層の帯を形成しています。加熱または冷却されると、一方の金属(真鍮)が他方の金属(スチール)よりも大きく膨張または収縮し、帯のコイル状の巻きがきつくなったり緩くなったりします。どちらのタイプの温度計にも、温度を示す目盛りが付いています。(credit a: modification of work by “dwstucke”/Flickr)
学習へのリンク
以下のデモンストレーション(http://openstaxcollege.org/l/16Bimetallic)では、コイル状に巻かれたバイメタルの帯の加熱と冷却の効果を見ることができます。
熱(q)は、温度が異なる2つの物体間の熱エネルギーの移動です。熱流(冗長な用語ですが、一般的に使われる用語です)は、一方の物体の熱エネルギーを増加させ、他方の物体の熱エネルギーを減少させます。まず最初に、高温(高い熱エネルギー)の物質(H)と低温(低い熱エネルギー)の物質(L)があるとします。Hの中の原子や分子は、Lの中の原子や分子よりも高い平均KEを有しています。もし私たちが物質Hと物質Lを接触させるように置いたならば、熱エネルギーは物質Hから物質Lに自然に流れるでしょう。物質Hの温度は低下し、その分子の平均KEも低下します。物質Lの温度は上昇し、その分子の平均KEも上昇します。2つの物質が同じ温度になるまで熱流は続きます(図5.6)。
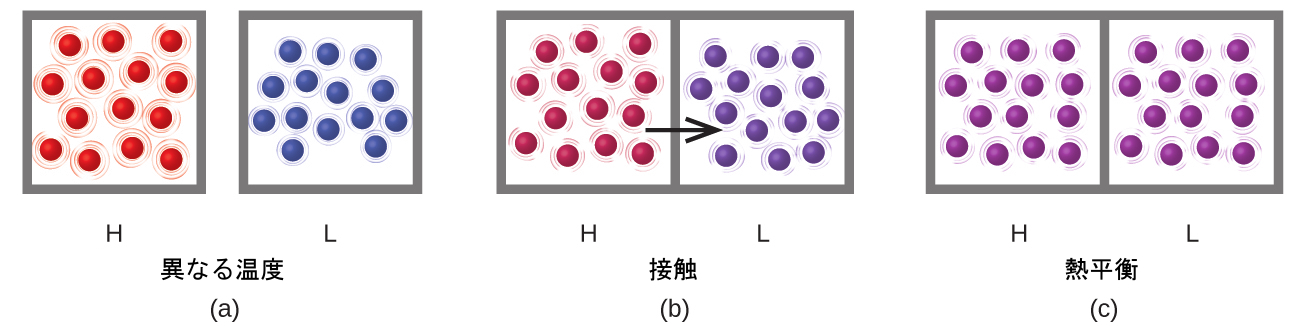
図5.6 | (a)物質Hと物質Lは最初は異なる温度であり、それらの原子は異なる平均運動エネルギーを有しています。(b)物質同士が接触すると、分子間の衝突により、高温の物質から低温の物質へと運動(熱)エネルギーの移動が生じます。(c)両方の物質が同じ温度にあり、その分子の平均運動エネルギーが同じであるとき、2つの物体は「熱平衡」に達します。
学習へのリンク
PhETシミュレーション(http://openstaxcollege.org/l/16PHETenergy)をクリックして、エネルギーの形態と変化を探求してください。エネルギーシステム(Energy Systems)タブに移動して、エネルギー源、変換方法、出力の組み合わせを作成してください。エネルギーシンボル(Energy Symbols)をクリックすると、エネルギーの移動を見ることができます。
化学反応や物理的な変化を受けた物質は、熱を放出したり吸収したりすることがあります。熱を放出する変化は発熱過程と呼ばれます。たとえば、酸素アセチレンのトーチを使ったときに起こる燃焼反応は発熱過程です。また、この過程では、トーチの炎が示すように、光という形態でエネルギーが放出されます(図5.7)。熱を吸収する反応や変化は吸熱過程です。痛めた筋肉の治療に使用される冷却パックは、吸熱過程の一例です。冷却パックの中の物質(水と硝酸アンモニウムなどの塩)が一緒になると、結果として起こる過程が熱を吸収して、冷たさの感覚を引き起こします。

図5.7 | (a)酸素アセチレントーチは、酸素の中でアセチレンを燃焼させることにより熱を発生させます。この発熱反応で放出されたエネルギーが金属を加熱し、融解させて切断します。火花は溶融した金属の小さな破片が飛び散ったものです。(b)冷却パックは、吸熱過程を利用して冷たさの感覚を作り出しています。(credit a: modification of work by “Skatebiker”/Wikimedia commons)
歴史的には、エネルギーはカロリー(cal)という単位で測定されていました。1カロリーは、1グラムの水を摂氏1度(1ケルビン)だけ上げるのに必要なエネルギーの量のことです。しかしながら、この量は大気圧や開始点の水の温度に依存します。カロリーはエネルギーの変化を簡単に測定できることから、現在でも頻繁に使用されています。大文字のCが付いたカロリー、つまり大カロリーは、食品のエネルギー含有量を定量化する際に一般的に用いられており、キロカロリーのことです。熱・仕事・エネルギーについてのSI単位はジュールです。1ジュール(J)とは、1ニュートンの力で物体を1メートル移動させたときに使われるエネルギー量と定義されています。これは、イングランドの物理学者ジェームズ・プレスコット・ジュールにちなんで名付けられました。1ジュールは 1 kg m²/s²に相当し、1ニュートンメートルとも呼ばれます。1キロジュール(kJ)は1000ジュールです。その定義を標準化するために、1カロリーは4.184ジュールに等しいとされています。
ここで、熱流や温度変化を記述するのに便利な2つの概念を紹介します。物体の熱容量(C)は、摂氏1度(すなわち1ケルビン)の温度変化(ΔT)を経験したときに吸収したり放出したりする熱(q)の量のことです:
\[ C =\frac{q}{ΔT} \]
熱容量は、熱を吸収したり放出したりする物質の種類と量によって決まります。したがって、それは示量性です。その値は物質の量に比例します。
たとえば、2つの鋳鉄製フライパンの熱容量を考えてみましょう。大きいフライパンの熱容量は小さいフライパンの熱容量の5倍です。なぜなら、両方とも同じ素材でできているにもかかわらず、大きいフライパンの質量が小さいフライパンの質量の5倍であるからです。質量が大きいということは、大きいフライパンの中に存在する原子が多いということを意味しており、その原子をすべて速く振動させるためには、より多くのエネルギーを必要とします。鋳鉄製の小さなフライパンの熱容量は、フライパンの温度を50.0°C上げるのに18150Jのエネルギーが必要であるという観察によってわかります:
\[ C_{小さなフライパン} ={\rm \frac{18140\ J}{50.0\ °C}= 363\ J/°C} \]
鋳鉄製の大きなフライパンは、同じ物質で作られているにもかかわらず、その温度を50.0 °C上げるために90700Jのエネルギーを必要とします。同じ温度変化をもたらすためには、素材の量が多い方が(比例して)大きな量のエネルギーを必要とするため、大きいフライパンの方が(比例して)大きな熱容量を持っています:
\[ C_{大きなフライパン} ={\rm \frac{90700\ J}{50.0\ °C}= 1814\ J/°C} \]
物質の比熱容量(c)は、一般に「比熱」と呼ばれており、物質1グラムの温度を摂氏1度(すなわち1ケルビン)だけ上げるのに必要な熱の量のことです:
\[ c =\frac{q}{mΔT} \]
比熱容量は、熱を吸収したり放出したりする物質の種類にのみ依存します。それは示強性です。重要なのは物質の種類であって量ではありません。たとえば、鋳鉄製の小さなフライパンの質量は808gです。したがって、鉄(フライパンを作るのに必要な物質)の比熱は:
\[ c_{鉄} ={\rm \frac{18140\ J}{(808\ g)(50.0\ °C)}= 0.449\ J/g °C} \]
大きなフライパンの質量は4040gです。私たちは、このフライパンのデータを使って鉄の比熱を計算することもできます:
\[ c_{鉄} ={\rm \frac{90700\ J}{(4040\ g)(50.0\ °C)}= 0.449\ J/g °C} \]
大きなフライパンは小さなフライパンよりも重いですが、どちらも同じ素材で作られているため、それらの比熱は同じ値(構築材料である鉄についての比熱)になります。比熱は、質量あたり温度あたりのエネルギーという単位で測定され、2つの示量性(熱と質量)の比から導き出される示強性であることに注意してください。モル熱容量とは、特定の物質の1モルあたりの熱容量であり、単位はJ/mol °Cです。モル熱容量も示強性です(図5.8)。

図5.8 | 大きなフライパンは質量が大きいので、小さなフライパンよりも大きな熱容量を有しています。それらは同じ素材でできているため、どちらのフライパンも同じ比熱を持っています。(credit: Mark Blaser)
水は比較的高い比熱(液体では約4.2 J/g °C、固体では約2.09 J/g °C)を持っています。ほとんどの金属は、はるかに低い比熱(通常1 J/g °C未満)を持っています。物質の比熱は温度によっていくらか変化します。しかしながら、この変動は通常は十分に小さく、この章で検討する温度範囲の中では、私たちは比熱を一定のものとして扱っていきます。いくつかの一般的な物質の比熱が表5.1に列挙されています。
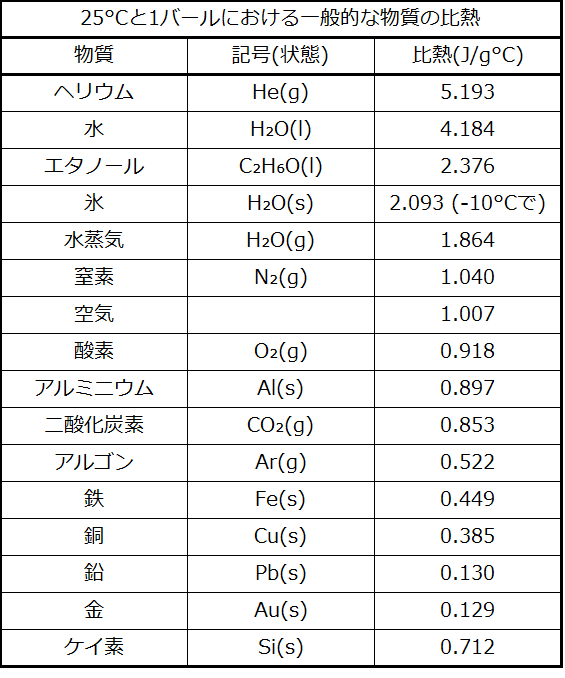
表5.1
もし私たちが物質の質量と比熱を知っていれば、熱を得たり失ったりする前後の温度変化を測定することによって、物質に出入りする熱の量(q)を決定することができます:
\[ q = (比熱)× (物質の質量)× (温度変化)\\ q = c× m× ΔT = c× m× (T_{\rm final} − T_{\rm initial}) \]
この式において、cは物質の比熱、mは物質の質量、ΔT(「デルタ・ティー」と読みます)は温度変化Tfinal - Tinitialです。物質が熱エネルギーを得る場合には、その温度は上昇し、最終温度は初期温度よりも高くなり、Tfinal - Tinitialは正の値を持ち、qの値は正の値となります。物質が熱エネルギーを失う場合には、その温度は低下し、最終温度は初期温度よりも低くなり、Tfinal - Tinitialは負の値を持ち、qの値は負の値となります。
例題5.1 熱を測定する
8.0×10²gの水を入れたフラスコを加熱し、水の温度を21°Cから85°Cまで上昇させました。この水はどれだけの熱を吸収しましたか?
解法
この質問に答えるためには、これらの因子を考えてください:
• 加熱される物質(この場合は水)の比熱
• 加熱される物質の量(この場合は8.0×10²g)
• 温度変化の大きさ(この場合は21°Cから85°C)
水の比熱は4.184J/g °Cなので、1gの水を1°Cだけ加熱するには4.184Jが必要です。1gの水を1°Cだけ加熱するには4.184Jが必要なので、8.0×10²gの水を1°Cだけ加熱するには800倍の量が必要になることに注意してください。最後に、1gの水を1°Cだけ加熱するのに4.184Jが必要なので、64°Cだけ加熱する(つまり、21°Cから85°Cまで加熱する)には64倍の量が必要になります。
これは、次の式でまとめることができます:
\[ \begin{eqnarray} q &=& c× m× ΔT = c× m× (T_{\rm final} − T_{\rm initial})\\ &=&{\rm (4.184\ J/g °C)× (8.0 × 10^2\ g)× (85 − 21)°C}\\ &=&{\rm (4.184\ J/g °C)× (8.0 × 10^2\ g)× (64)°C}\\ &=&{\rm 210000\ J\ ( = 2.1 ×10^2\ kJ)} \end{eqnarray} \]
温度が上がっているため、水は熱を吸収しており、qは正の値になります。
学習内容の確認
502gの鉄製スキレットの温度を25 °Cから250 °Cに上昇させるには、どれだけの熱(ジュールで)を加えなければなりませんか? 鉄の比熱は0.449J/g °Cです。
解答:5.12 × 10⁶J
熱、比熱、質量、および温度変化の間の関係性は、これらの量のうち3つが既知であるか、または推定できる場合には、残りの1つのどれでも(熱だけではなく)を決定するために使用できることに注意してください。
例題5.2 他の量を決定する
ある未知の金属片は、重さが348gあります。この金属片が6.64 kJの熱を吸収すると、その温度は22.4 °Cから43.6 °Cに上昇しました。この金属の比熱を決定してください(それは金属の正体を知る手がかりになるかもしれません)。
解法
この金属の質量、熱、温度変化がわかっているため、私たちはこの関係性を用いて比熱を決定することができます:
\[ q = c× m× ΔT = c× m× (T_{\rm final} − T_{\rm initial}) \]
既知の値を代入すると:
\[ {\rm 6640\ J} = c× {\rm (348\ g)× (43.6 − 22.4)\ °C} \]
これを解くと:
\[ c =\rm \frac{6640\ J}{(348\ g)× (21.2\ °C)}= 0.900\ J/g °C \]
この値を表5.1の値と比較すると、この値はアルミニウムの比熱と一致しており、未知の金属がアルミニウムであるかもしれないことを示唆しています。
学習内容の確認
ある未知の金属片は、重さが217gあります。この金属片が1.43 kJの熱を吸収すると、その温度は24.5 °Cから39.1 °Cに上昇しました。この金属の比熱を決定して、その正体を予測してください。
解答:c = 0.451 J/g °C。この金属は鉄である可能性が高いです。
日常生活の中の化学
太陽熱エネルギー発電所
地球に届く太陽光には、私たちが現在捕らえているエネルギーの何千倍ものエネルギーが含まれています。太陽熱システムは、太陽からのエネルギーを私たちが利用可能なエネルギーへと変換するという問題への1つの可能な解決策を与えてくれます。大規模な太陽熱発電所の設計仕様はさまざまですが、すべての太陽熱発電所は太陽光を集めて物質を加熱し、その物質の中に「蓄えられた」熱を電気に変換します。
アリゾナ州ソノラ砂漠にあるソラナ発電所では、280メガワットの電力を生産しています。この発電所では、パラボラ状の鏡を使って、熱伝達流体(HTF)で満たされたパイプに太陽光を集光します(図5.9)。HTFは2つの働きをします:HTFは、水を蒸気に変え、この蒸気がタービンを回転させ、それが今度は電気を発生させます。またHTFは、塩類の混合物を溶かして加熱し、その混合物は熱エネルギー貯蔵システムとして機能します。日が沈んだ後、溶融した塩類の混合物は、蒸気を発生させてタービンを6時間稼働させるのに十分なほどの熱を放出することができます。溶融した塩類は、高い熱容量と熱伝導率など、多くの利点を持っているために使用されています。
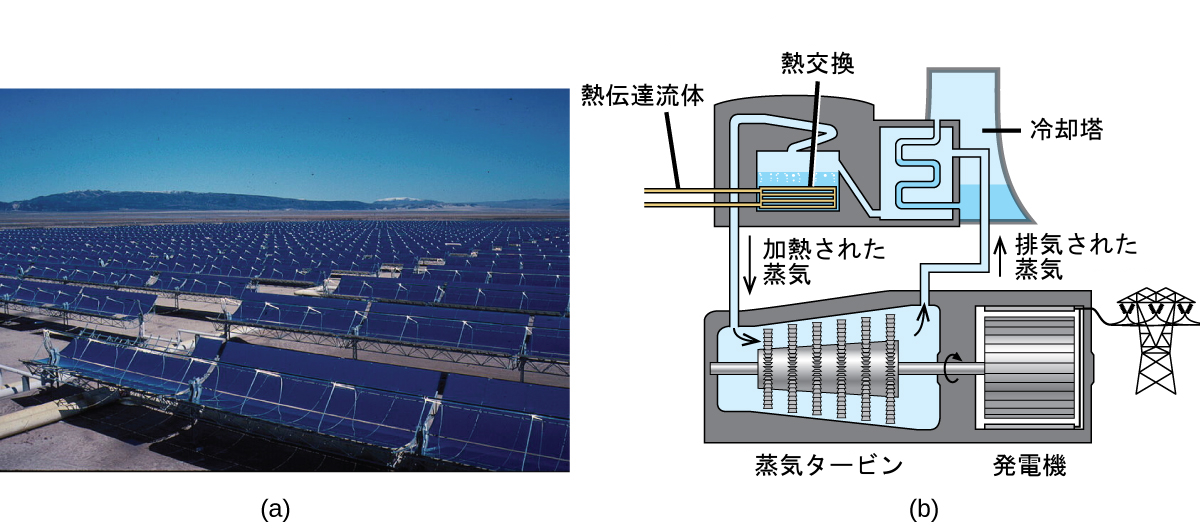
図5.9 | この太陽熱発電所では、パラボラ状のU字型の鏡を用いて太陽光を集光しています。(credit a: modification of work by Bureau of Land Management)
カリフォルニア州モハーベ砂漠にある377メガワットを発電するイヴァンパ太陽熱発電システムは、世界最大の太陽熱発電所です(図5.10)。17万枚の鏡が水で満たされた3本の塔に大量の太陽光を集め、538°C以上の蒸気を発生させ、それが発電用タービンを駆動させています。そこは、14万軒の家庭に電力を供給するのに十分なエネルギーを生み出しています。水は熱容量と蒸発熱が大きいため、運用上の流体として使用されています。

図5.10 | (a)イヴァンパ太陽熱発電所では、17万枚の鏡を使って水で満たされた塔に太陽光を集中させています。(b)この発電所は、モハーベ砂漠付近およびカリフォルニア州とネバダ州の境界付近にある4000エーカーの公有地に広がっています。(credit a: modification of work by Craig Dietrich; credit b: modification of work by “USFWS Pacific Southwest Region”/Flickr)
5.2 熱量測定
この節が終わるまでに、あなたは次のことができるようになります:
•熱量測定の技術を説明する
•典型的な熱量測定データを使用して熱と関連する性質を計算し、解釈する
私たちが化学的または物理的なプロセスに関与する熱の量を測定するために使用することができる技術の1つは、熱量測定として知られています。熱量測定は、物質へと伝達される、または物質から伝達される熱の量を測定するために使用されます。そのためには、あらかじめ調整された物体(熱量計)と熱を交換します。熱量計で測定された温度変化から、研究対象のプロセスによって伝達される熱の量を導き出します。このアプローチを使って熱伝達を測定するには、系(化学的または物理的変化を受ける物質)とその周囲(系に熱を供給するか、系から熱を吸収するかのいずれかの役割を果たす、測定装置の構成要素を含む他のすべての物質)を定義する必要があります。
熱量計は、化学的または物理的プロセスに関与する熱の量を測定するために使用される装置です。たとえば、ある熱量計の中の溶液中で発熱反応が起こると、反応によって生じた熱が溶液によって吸収され、溶液の温度が上昇します。吸熱反応が起こると、必要な熱が溶液の熱エネルギーから吸収され、溶液の温度が低下します(図5.11)。この温度変化と溶液の比熱や質量を使って、両方の場合において関連する熱の量を計算することができます。
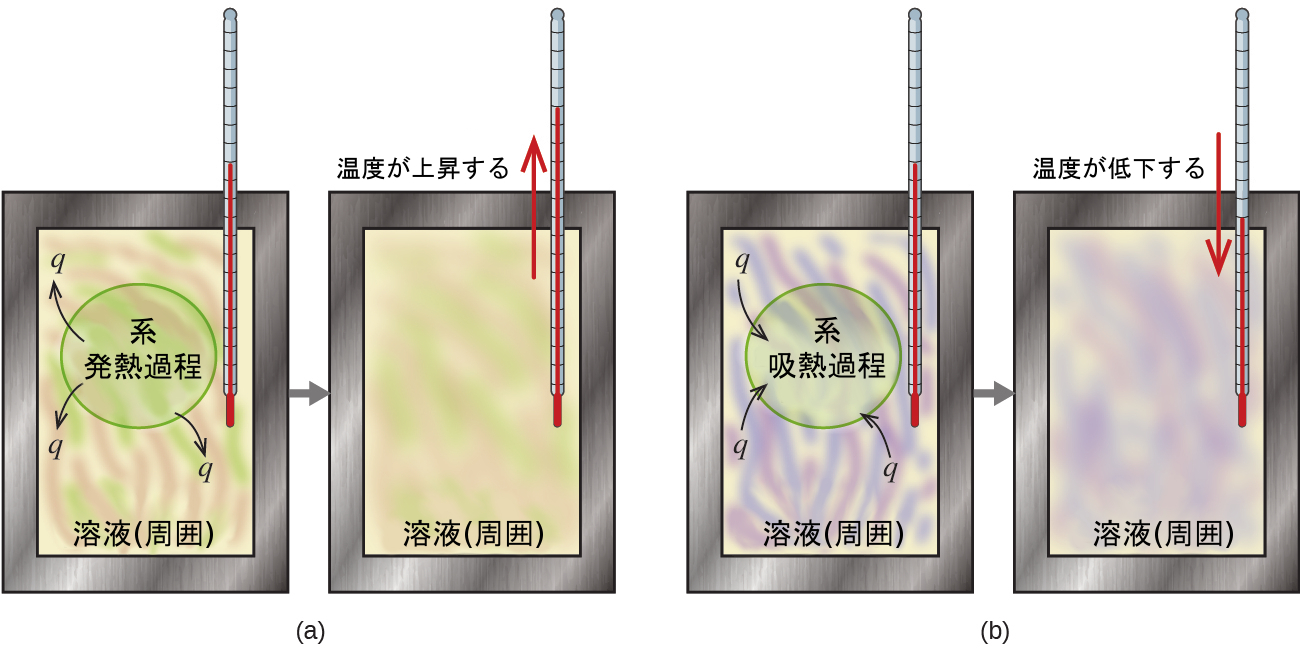
図5.11 | 熱量測定では、(a)発熱過程が発生して熱qが負となる(熱エネルギーが系からその周囲に移動していることを示します)か、または、(b)吸熱過程が発生して熱qが正となる(熱エネルギーが周囲から系に移動していることを示します)かのいずれかです。
科学者は、熱量計とその環境との間の熱の移動をすべて防ぐことができる、十分に断熱された熱量計を使用しています。これは、「周囲」を、実質的に熱量計の系以外の構成要素(および熱量計自体)に限定します。これにより、化学プロセスに関与する熱や、食品のエネルギー含有量などを正確に決定することができます。一般的な化学の学生は、しばしばポリスチレン製のカップからなる簡単な熱量計を使います(図5.12)。このような使いやすい「コーヒーカップ」型の熱量計は、外部環境との熱交換が多いため、さほど正確でないエネルギー値しか得られません。
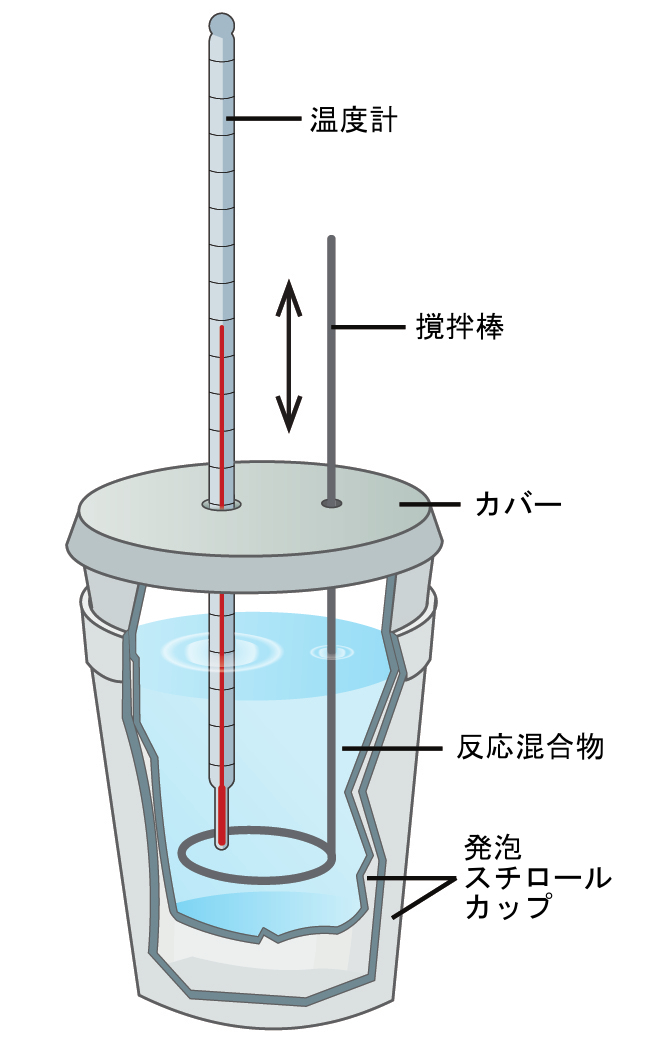
図5.12 | 2つのポリスチレンカップから簡単な熱量計を作ることができます。温度計と撹拌棒がカバーを通って反応混合物の中へと伸びています。
市販の溶液熱量計も利用できます。比較的安価な熱量計は、しばしば、使用中の熱接触を最小限に抑えるように入れ子状に配置された2つの薄肉のカップと、断熱カバー、手で動かす撹拌棒、および単純な温度計で構成されています。より高価な、産業用や研究用に使用される熱量計は、一般的によく断熱された完全密閉型の反応容器、電動撹拌機構、より正確な温度センサーを備えています(図5.13)。
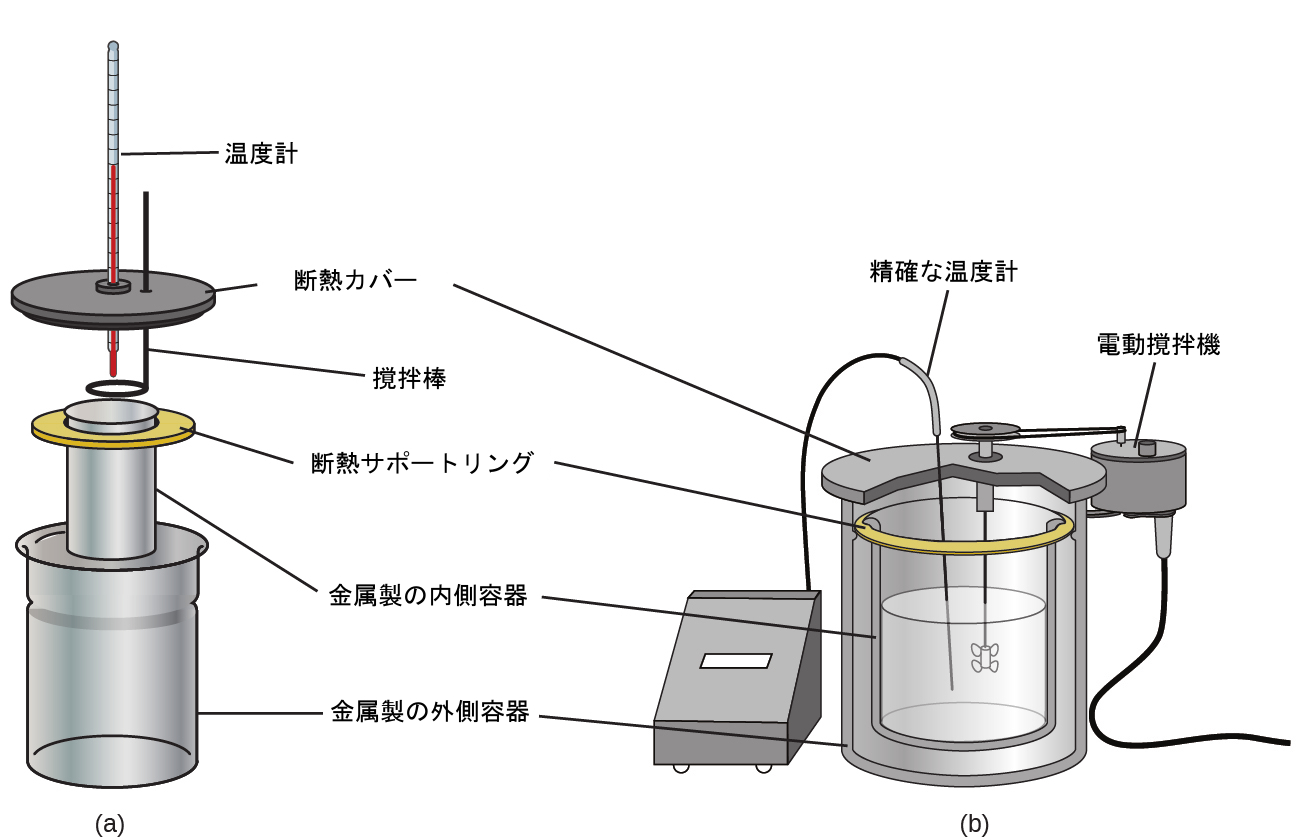
図5.13 | 市販の溶液熱量計には、(a)学生用のシンプルで安価なモデルから、(b)産業用や研究用の高価で高精度なモデルまでさまざまな種類があります。
化学反応の熱量測定を議論する前に、熱量測定の背後にある核となる考え方を説明してくれる簡単な例を考えてみましょう。最初に、高温の金属片(M)などといった高温物質と、低温の水(W)などといった低温物質があるとします。もし私たちが金属を水の中に入れると、MからWに熱が移動します。2つの物質が同じ温度になるまで、すなわち、それらが熱平衡に達するまで、Mの温度は下がり、Wの温度は上がります(図5.14)。これが熱量計の中で行われる場合、理想的には2つの物質間ですべての熱伝達が起こり、その外部環境によって熱が得られたり失われたりすることはありません。この理想的な状況下では、正味の熱変化はゼロです:
\[ q_{\rm 物質 M} + q_{\rm 物質 W} = 0 \]
この関係性は、物質Mによって得られる熱が物質Wによって失われる熱に等しいことを示すように並べ替えることができます:
\[ q_{\rm 物質 M} = −q_{\rm 物質 W} \]
したがって、熱(変化)の大きさはどちらの物質にとっても同じであり、負の符号は単にq物質Mとq物質Wが熱流の方向(獲得または損失)が逆であることを示しているだけで、どちらか一方のqの値の算術的な符号を示すものではありません(それは、定義に従って、問題となっている物質が熱を得るか失うかによって決定されます)。ここで記述された特定の状況では、熱はMからWに移動するので、q物質Mは負の値であり、q物質Wは正の値です。
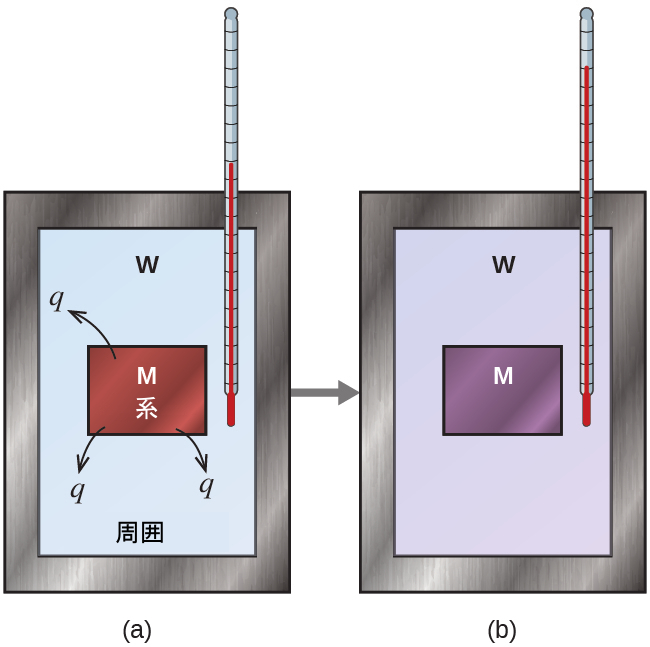
図5.14 | 単純な熱量測定プロセスでは、(a)熱qは、高温の金属Mから低温の水Wに伝わり、(b)両者が同じ温度になります。
例題5.3 温度の異なる物質間の熱伝達
360.0gの鉄筋(コンクリートの補強に使用するスチールの棒)の一片を24.0°Cの水425mLの中に沈めます。水の最終的な温度は42.7°Cと測定されました。鉄筋の一片の初期の温度を計算してください。スチールの比熱は鉄の比熱とほぼ同じであり(表5.1)、すべての熱伝達は鉄筋と水の間で起こっている(周囲との熱交換はない)と仮定してください。
解法
水の温度は24.0°Cから42.7°Cに上昇するので、水は熱を吸収します。その熱は、最初はより高い温度であった鉄筋の一片からもたらされました。すべての熱伝達が鉄筋と水の間で行われ、外部環境に「失われた」熱がないと仮定すると、鉄筋によって放出された熱 = -水によって取り込まれた熱、すなわち:
\[ q_{鉄筋} = −q_{水} \]
私たちは熱が他の測定可能な量とどのように関係しているかを知っているため、私たちは以下を得ます:
\[ (c× m× ΔT)_{鉄筋} = −(c× m× ΔT)_{水} \]
f = 最終、i = 初期として、拡張するとこのようになります:
\[ c_{鉄筋} × m_{鉄筋} × (T_{\rm f,鉄筋} − T_{\rm i,鉄筋}) = −c_{水} × m_{水} × (T_{\rm f,水} − T_{\rm i,水}) \]
水の密度は1.0 g/mLなので、水の425 mL = 425 gです。鉄筋と水は両方とも最終温度が42.7 °Cであることに注意して、既知の値を代入すると、以下が得られます:
\[ (0.449\ {\rm J/g °C})(360.0\ {\rm g})(42.7\ {\rm °C} − T_{\rm i,鉄筋}) = −(4.184\ {\rm J/g °C})(425\ {\rm g})(42.7\ {\rm °C} − 24.0\ {\rm °C})\\ T_{\rm i,鉄筋} =\rm \frac{(4.184\ J/g °C)(425\ g)(42.7\ °C − 24.0\ °C)}{(0.449\ J/g °C)(360.0\ g)}+ 42.7\ °C \]
これを解くと、Ti,鉄筋 = 248 °Cとなりますので、鉄筋の初期温度は248 °Cでした。
学習内容の確認
248gの銅片を22.6°Cの水390mLの中に沈めます。水の最終的な温度は 39.9 °Cと測定されました。銅片の初期の温度を計算してください。すべての熱伝達は銅と水の間で起こっていると仮定してください。
解答:銅の初期温度は335.6°Cでした。
学習内容の確認
初期の温度が314 °Cである248gの銅片を、初期の温度が22.6°Cである390mLの水の中に沈めます。すべての熱伝達が銅と水の間で起こると仮定して、最終的な温度を計算してください。
解答:(銅と水の両方が到達する)最終温度は38.7°Cです。
この方法は、未知の金属の比熱のような他の量を決定するために使用することもできます。
例題5.4 比熱測定による金属の特定
沸騰した水に浸けてあった59.7gの金属片を、22.0°Cの水60.0mLの中に素早く移しました。最終的な温度は28.5 °Cとなりました。これらのデータを使用して、この金属の比熱を決定してください。その結果を使用して金属を特定してください。
解法
熱伝達が完全であると仮定すると、金属によって放出された熱 = -水によって取り込まれた熱、すなわち:
\[ q_{金属} = −q_{水} \]
拡張された形では、以下のようになります:
\[ c_{金属} × m_{金属} × (T_{\rm f,金属} − T_{\rm i,金属}) = −c_{水} × m_{水} × (T_{\rm f,水} − T_{\rm i,水}) \]
金属は沸騰した水に浸かっていたので、その初期温度は100.0°Cであり、水は60.0mL=60.0gであることに注目すると、私たちは以下を得ます:
\[ (c_{金属})\rm (59.7\ g)(28.5\ °C − 100.0\ °C) = −(4.18\ J/g °C)(60.0\ g)(28.5\ °C − 22.0\ °C) \]
これを解くと:
\[ c_{金属} =\rm \frac{−(4.184\ J/g °C)(60.0\ g)(6.5\ °C)}{(59.7\ g)(−71.5\ °C)}= 0.38\ J/g °C \]
これを表5.1の値と比較すると、私たちの実験で得られた比熱は銅の値(0.39 J/g °C)に最も近いので、私たちはこの金属が銅であると特定します。
学習内容の確認
92.9gの銀/灰色の金属片を178.0°Cに加熱し、24.0°Cの水75.0mLの中に素早く移しました。5分後、金属と水の両方が同じ温度(29.7 °C)に達しました。比熱と金属の正体を決定してください。(注: 比熱は2つの異なる金属の比熱に近いことがわかるはずです。あなたがどのようにして自信を持って金属の正体を決定できるか説明してください。)
解答:c金属 = 0.13 J/g °C:この比熱は、金または鉛の比熱に近いです。数値だけに基づいてどちらの金属かを判断するのは難しいでしょう。しかしながら、比熱の値に加えて、この金属が銀/灰色であるという観察から、この金属が鉛であることがわかります。
熱量計を使って化学反応に関わる熱を決定する場合も、これまで議論してきたものと同じ原理が適用されます。熱量計が吸収する熱の量はしばしば無視できるほど小さく(ただし後で議論するように、高精度の測定ではそうすることはできません)、熱量計は外部環境とのエネルギー交換を最小限に抑えることができます。化学反応ではエネルギーが作られたり破壊されたりすることはないので、反応(「系」)で生成または消費された熱q反応と、溶液(「周囲」)によって吸収または失われた熱q溶液を足し合わせると、ゼロにならなければなりません:
\[ q_{反応} + q_{溶液} = 0 \]
これは、反応で生成または消費される熱の量が、溶液に吸収または失われる熱の量に等しいことを意味します:
\[ q_{反応} = −q_{溶液} \]
この概念は、すべての熱量測定の問題と計算の中心にあります。
例題5.5 発熱反応によって生成される熱
コーヒーカップ型の熱量計に1.00 MのHCl(aq)50.0 mLと1.00 MのNaOH(aq)50.0 mL(両方とも22.0°C)を加えると、混合物の温度は最高で28.9°Cに達しました。この反応によって発生する熱のおおよその量は何ですか?
\[ \rm HCl\ (aq) + NaOH\ (aq) ⟶ NaCl\ (aq) + H_2O\ (l) \]
解法
何が起こっているのかを明確にするために、2つの溶液が混ざっている間に反応が起こらないように2つの溶液を素早く混ぜ合わせ、混ざった後に反応が起こったと想像してみてください。混合の瞬間には、22.0 °CのHClとNaOHの混合物100.0 mLがあります。その後、溶液の温度が28.9 °Cに達するまでHClとNaOHが反応します。
反応によって放出された熱は、溶液によって取り込まれた熱と等しいです。したがって:
\[ q_{反応} = -q_{溶液} \]
(この関係性は、熱量計が反応からの熱を吸収せず、熱量計と外部環境との間で熱交換がない場合にのみ成立するということを覚えておくことが重要です。)
次に、私たちは、溶液によって吸収される熱は、その比熱、質量、温度変化に依存することを知っています:
\[ q_{溶液} = (c× m× ΔT)_{溶液} \]
この計算を進めるためには、私たちはもういくつかの合理的な仮定や近似を行う必要があります。この溶液は水溶液であるため、私たちは比熱と質量の値に関しては、この溶液を水であるかのようにして計算を進めることができます。水の密度は約1.0g/mLなので、100.0mLの質量は約1.0×10²gとなります(2つの有効数字)。水の比熱は約4.184 J/g °Cなので、私たちはこれを溶液の比熱として使います。これらの値を代入すると:
\[ q_{溶液} =\rm (4.184\ J/g °C)(1.0 × 10^2\ g)(28.9\ °C − 22.0\ °C) = 2.9 × 10^3\ J \]
最後に、私たちは反応の熱を求めようとしているので、以下を得ます:
\[ q_{反応} = −q_{溶液} = \rm −2.9× 10^3\ J \]
負の符号は、反応が発熱性であることを示しています。この反応では2.9 kJの熱が発生します。
学習内容の確認
コーヒーカップ型の熱量計の中で0.200 MのNaCl(aq)100 mLと0.200 MのAgNO₃(aq)100 mL(両方とも21.9°C)を混合すると、温度は23.5°Cまで上昇し、固体のAgClが生成しました。この沈殿反応によってどれだけの熱が発生しましたか?また、どのような仮定をして値を決定しましたか?
解答:1.34 × 10³J。熱量計によって熱が吸収されることがなく、熱量計とその周囲との間で熱の交換がなく、溶液の比熱と質量が水の比熱と質量と同じであると仮定します。
日常生活の中の化学
ハンドウォーマーの熱化学
あなたは寒い日に屋外で仕事をしたり、遊んだりするとき、手を温めるためにハンドウォーマーを使ったことがあるでしょう(図5.15)。一般的な再利用可能なハンドウォーマーには、NaC₂H₃O₂(酢酸ナトリウム)の過飽和溶液と金属製の円盤が入っています。ディスクを曲げると核生成の部位ができ、その周りで準安定なNaC₂H₃O₂が素早く結晶化します(後の溶液に関する章では、飽和と過飽和についてより詳しく調べていきます)。NaC₂H₃O₂(aq)⟶ NaC₂H₃O₂(s) の過程は発熱性であり、この過程で生成された熱はあなたの手に吸収され、手を温めます(少なくともしばらくの間は)。もしこのハンドウォーマーを再加熱すると、NaC₂H₃O₂は再溶解して再利用することができます。

図5.15 | 化学的なハンドウォーマーは、寒い日にあなたの手を温める熱を発生させます。このハンドウォーマーでは、発熱性の沈殿反応を起こす金属の円盤が見えます。(credit: modification of work by Science Buddies TV/YouTube)
もう1つの一般的なハンドウォーマーは、それを開封したときに、ハンドウォーマーの中の鉄と水が空気中の酸素にさらされることで熱を発生させます。この発熱反応を簡略化したものが4Fe(s) + 3O₂(g) ⟶ 2Fe₂O₃(s)です。ハンドウォーマーに含まれる塩が反応を触媒するので、より急速に熱を発生させます。セルロース、バーミキュライト、活性炭は熱を均等に分散させるのに役立ちます。他のタイプのハンドウォーマーには、点火液(白金触媒が点火液の発熱酸化を助けます)、炭(炭は特殊な場合に酸化します)、または電池から抵抗線に電流を流して熱を発生させる電気ユニットが使用されています。
学習へのリンク
このリンク(http://openstaxcollege.org/l/16Handwarmer)は、化学的なハンドウォーマーの中にある円盤を曲げたときに発生する沈殿反応を示しています。
例題5.6 瞬間冷却パックの熱流
固体の硝酸アンモニウムが水に溶解すると、溶液は冷たくなります。これが「瞬間冷却パック」の基本です(図5.16)。熱量計の中で3.21 g の固体NH₄NO₃が50.0 gの水(24.9 °C)に溶解したとき、温度が20.3 °C に低下しました。
この反応のqの値を計算し、その算術符号の意味を説明してください。仮定したことがあれば、それを述べてください。

図5.16 | 瞬間冷却パックは、固体の硝酸アンモニウムの入った袋と水の入った2つ目の袋で構成されています。硝酸アンモニウムの溶解は水から熱エネルギーを奪う吸熱過程であるため、水の袋を破るとパックは冷たくなります。そして、冷えたパックはあなたの体から熱エネルギーを奪います。
解法
私たちは、熱量計が溶液とその外部環境(熱量計自体を含む)との間の熱伝達を阻止していると仮定します。その場合:
\[ q_{\rm rxn} = −q_{\rm soln} \]
であり、「rxn」と「soln」はそれぞれ「反応」と「溶液」の略語として使用されています。
また、溶液の比熱が水の比熱と同じであると仮定すると、以下のようになります:
\[ \begin{array}{ll} q_{\rm rxn} = −q_{\rm soln} = −(c× m× ΔT)_{\rm soln}\\ \rm = −[(4.184\ J/g °C)× (53.2\ g)× (20.3\ °C − 24.9\ °C)]\\ \rm = −[(4.184\ J/g °C)× (53.2\ g)× (−4.6\ °C)]\\ \rm = +1.0 × 10^3\ J = +1.0\ kJ \end{array} \]
qの正の符号は、溶解が吸熱過程であることを示しています。
学習内容の確認
コーヒーカップ型の熱量計の中で3.00gのKCl試料を3.00×10²gの水に加えたとき、温度が1.05°C低下しました。KClの溶解にはどれだけの熱が関与していますか?また、あなたはどのような仮定をしましたか?
解答:1.33 kJ。熱量計が溶液と外部環境(熱量計自体を含む)との間の熱伝達を阻止し、溶液の比熱が水の比熱と同じであると仮定します。
熱量計によって吸収される熱の量が大きすぎて無視できない場合や、私たちがより正確な結果を必要としている場合には、私たちは溶液と熱量計の両方によって吸収される熱の量を考慮しなければなりません。
ここまで説明した熱量計は、定圧(大気圧)で動作するように設計されており、溶液中で発生する過程に伴う熱流を測定するのに便利です。また、燃焼反応のように多量の熱や気体状の生成物が得られる反応によって生じるエネルギーを測定するために、一定の体積で動作する別のタイプの熱量計(通称「ボンベ熱量計」として知られています)が使用されています。(「ボンベ(爆弾)」という用語は、このような反応が、他の熱量計であれば破損してしまうほどの爆発に似た激しい反応であるという観察に由来します。)このタイプの熱量計は、反応物を収容する頑丈な鋼鉄製の容器(「ボンベ」)からなります。この容器自体が水に沈められています(図5.17)。試料はボンベの中に入れられ、ボンベは高圧の酸素で満たされます。小さな電気スパークを使って試料に点火します。反応によって発生したエネルギーは、鋼鉄製のボンベと周囲の水に吸収されます。温度上昇が測定され、すでに分かっている熱量計の熱容量と合わせて、反応によって生成されたエネルギーを計算するために使用されます。ボンベ熱量計は、熱量計の熱容量を決定し、正確な結果を得るために校正が必要です。この校正は、既知のq(安息香酸をニッケル導火線からの火花で点火して反応の前後で重量を測定したときの測定値など)を伴う反応を用いて行われます。既知の反応によって生じる温度変化は、熱量計の熱容量を決定するために使用されます。この校正は、通常、研究データを収集するために熱量計を使用する前に毎回行います。
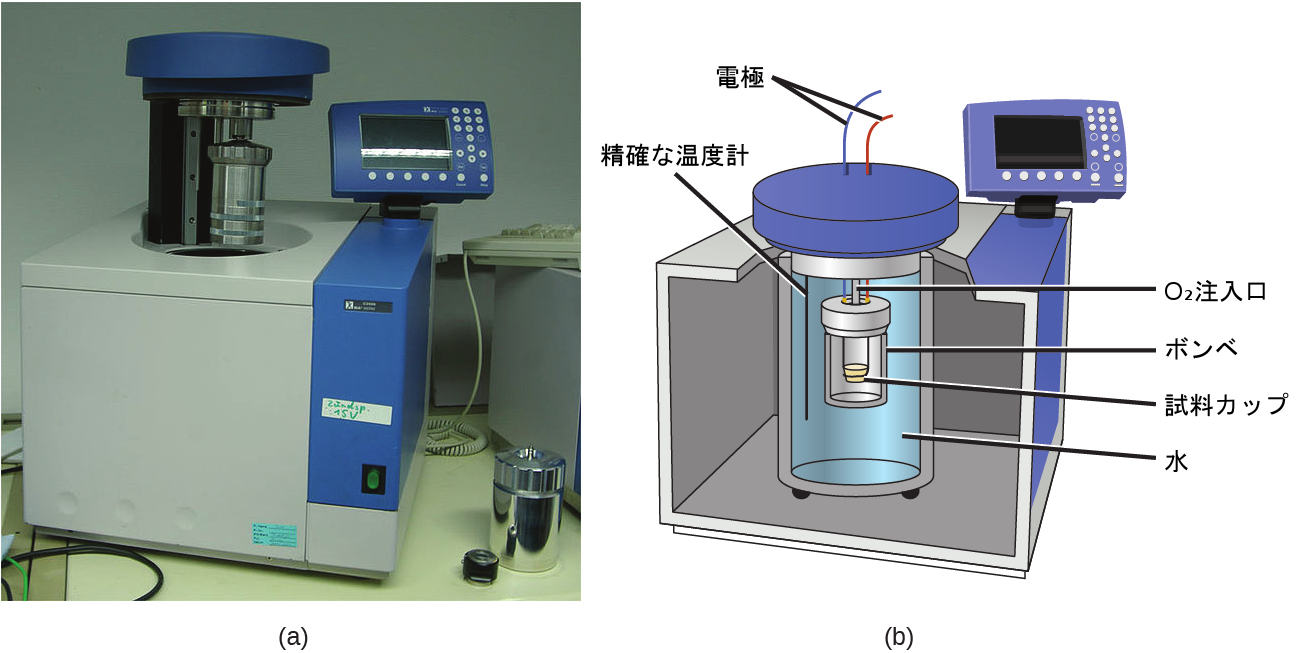
図5.17 | (a)ボンベ熱量計は、燃焼などといった気体状の反応物や生成物を含む反応によって生じる熱を測定するために使用されます。(b)反応物は、水の中に沈められ断熱材料で囲まれた気体密閉型の「ボンベ」の中に入っています。(credit a: modification of work by “Harbor1”/Wikimedia commons)
学習へのリンク
このリンク(http://openstaxcollege.org/l/16BombCal)をクリックすると、ボンベ熱量計を動作させるためにどのように準備をしているかを見ることができます。
このサイト(http://openstaxcollege.org/l/16Calorcalcs)では、サンプルデータを用いた熱量計算方法を示しています。
例題5.7 ボンベ熱量計
3.12gのグルコース(C₆H₁₂O₆)をボンベ熱量計の中で燃焼させると、熱量計の温度が23.8°Cから35.6°Cに上昇しました。熱量計には 775 g の水が入っており、ボンベ自体の熱容量は 893 J/°Cです。グルコース試料の燃焼によってどれだけの熱が発生したでしょうか?
解法
燃焼により発生する熱は、主として水とボンベによって吸収されます。(反応生成物や未反応の過剰な酸素によって吸収される熱の量は比較的小さく、それらを扱うことは、この教科書の範囲を超えています。私たちは計算ではそれらを無視することにします。)
反応によって生じた熱は水とボンベに吸収されます:
\[ \begin{array}{ll} q_{\rm rxn} = −(q_{水} + q_{ボンベ})\\ \rm = −[(4.184\ J/g °C)× (775\ g)× (35.6\ °C − 23.8\ °C) + 893\ J/°C× (35.6\ °C − 23.8\ °C)]\\ \rm = −(38300\ J + 10500\ J)\\ \rm = −48800\ J = −48.8\ kJ \end{array} \]
3.12gのグルコースを燃焼させたとき、この反応は48.8kJの熱を放出しました。
学習内容の確認
0.963gのベンゼン(C₆H₆)をボンベ熱量計の中で燃焼させると、熱量計の温度は8.39°Cだけ上昇しました。このボンベの熱容量は 784 J/°Cで、925 mL の水の中に沈められています。ベンゼン試料の燃焼によってどれだけの熱が発生したでしょうか?
解答:39.0 kJ
1899年に最初のものが作られて以来、生きている人間によって生み出される熱を測定するために35種類もの熱量計が作られてきました。[2]これらのさまざまなデザインの全身熱量計は、人間1人が入るのに十分な大きさがあります。最近では、比較的通常の活動を行うことができる部屋全体の熱量計が登場し、それらの熱量計は、実世界をより密接に反映するようなデータを生み出しています。これらの熱量計は、異なる環境条件、異なる食生活、糖尿病のような異なる健康状態の下での個人の代謝を測定するために使用されています。人間の場合、代謝は通常、1日あたりの大カロリーで測定されます。栄養カロリー(大カロリー)とは、食品の代謝に由来するエネルギー量を定量化するために使われるエネルギー単位です。1大カロリーは1000カロリー(1kcal)に相当し、1kgの水を1°Cだけ加熱するのに必要なエネルギーの量です。
日常生活の中の化学
栄養カロリーを測定する
あなたの日常生活では、食品に含まれるエネルギーの量を数値化するために使用されている大カロリー、つまり栄養カロリーで与えられるエネルギーの方がなじみがあるかもしれません。1カロリー(cal)は正確に4.184ジュールであり、1大カロリー(大文字のCalorieであることに注意)は1000cal、つまり1kcalです。(これは、1kgの水を1°Cだけ加熱するのに必要なエネルギー量に大体相当します。)
食品の主要栄養素は、タンパク質、炭水化物、および、脂肪または油です。タンパク質は1グラムあたり約4大カロリー、炭水化物も1グラムあたり約4大カロリーを与え、脂肪と油は約9大カロリー/gを与えます。食品の包装に貼られている栄養表示ラベルには、1食分のカロリー含有量と、3つの主要栄養素のそれぞれに由来する大カロリーの内訳が示されています(図5.18)。
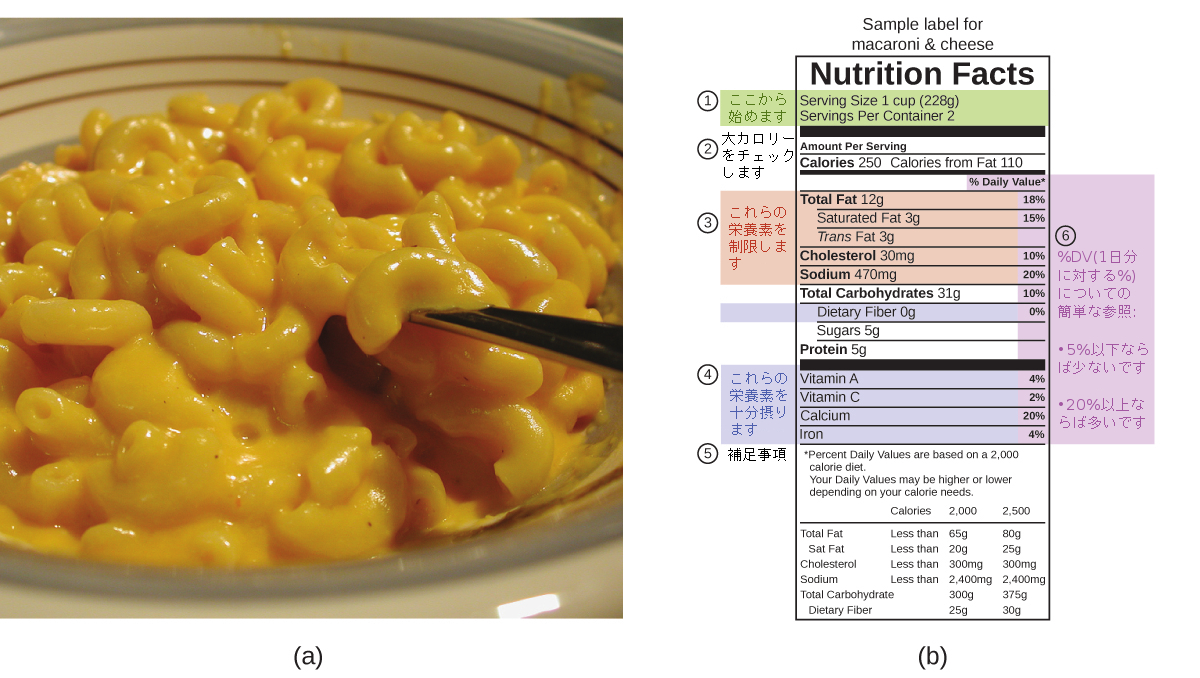
図5.18 | (a)マカロニとチーズには、その食品の中の主要栄養素の形態でエネルギーが含まれています。(b)食品の栄養情報は包装ラベルに記載されています。米国ではエネルギー含有量は大カロリー(1食あたり)で示されていますが、それ以外の国では通常キロジュールが使われています。(credit a: modification of work by “Rex Roof”/Flickr)
(b)に示されている例では、228gの分量あたりの総エネルギーは以下のように計算されます:
\[ \begin{array}{ll} \rm (5\ g\ タンパク質 × 4\ 大カロリー/g)\\ \rm + (31\ g\ 炭水化物× 4\ 大カロリー/g)\\ \rm + (12\ g\ 脂肪 × 9\ 大カロリー/g)\\ = 252\ 大カロリー \end{array} \]
このように、私たちは食品ラベルを使って大カロリーを数えることができます。しかし、その数値はどこから出てくるのでしょうか?そして、どれくらい正確なのでしょうか?食品のカロリー含有量は、ボンベ熱量測定法を使うことによって、すなわち、食品を燃やして、そこに含まれるエネルギーを測定することによって決定できます。食品の試料を計量し、ミキサーで混合し、フリーズドライし、粉末に粉砕してペレット状に形成します。このペレットをボンベ熱量計の中で燃焼させ、温度変化を測定して食品1グラムあたりのエネルギーに換算します。
現在、食品表示ラベルのカロリー含有量は、食品のさまざまな化学成分であるタンパク質、炭水化物、脂肪の平均的なカロリー含有量を使用するアトウォーター方式と呼ばれる方法を用いて算出されています。平均量は式で与えられたもので、食品全体のボンベ熱量測定で得られたさまざまな結果から導き出されたものです。炭水化物の量は、難消化性炭水化物である食物繊維の含有物の所定の量について割り引いたものです。食品のエネルギー量を求めるには、炭水化物、タンパク質、脂肪の量にそれぞれ1グラムあたりの平均大カロリーを掛け合わせ、その積を合計して総エネルギー量を得ます。
学習へのリンク
このリンク(http://openstaxcollege.org/l/16USDA)をクリックすると、8000以上の食品の栄養情報を含む米国農務省(USDA)の国家栄養データベースにアクセスすることができます。
5.3 エンタルピー
この節が終わるまでに、あなたは次のことができるようになります:
•熱力学の第一法則を述べる
•エンタルピーを定義し、その状態関数としての分類を説明する
•熱化学方程式を書いてバランスを取る
•さまざまな化学反応のエンタルピー変化を計算する
•ヘスの法則を説明し、それを使用して反応エンタルピーを計算する
熱化学は化学熱力学の一分野であり、化学的および物理的プロセスの文脈で熱や仕事、その他のエネルギーの関係性を扱う科学です。この章で私たちが熱化学に集中するにあたり、私たちは熱力学で広く使われている概念のいくつかを考える必要があります。
物質はエネルギーの貯蔵庫として機能します。これは、エネルギーは物質に加えられたり、物質から取り除かれたりすることがある、ということを意味します。物質の原子や分子の運動エネルギーが上昇するときに、エネルギーは物質に蓄えられます。より大きな運動エネルギーは、原子や分子の並進(移動すなわち直線運動)、振動、または回転の増加の形であるかもしれません。熱エネルギーが失われると、これらの動きの強さが低下し、運動エネルギーが低下します。物質に存在するあらゆる種類のエネルギーの合計は内部エネルギー(U)と呼ばれます。これは、Eという記号で表されることもあります。
系が変化を受けると、その内部エネルギーが変化し、系から周囲へ、あるいは周囲から系へとエネルギーが移動します。エネルギーは、系が周囲から熱(q)を吸収するとき、または周囲が系に仕事(w)をするときに、系に伝達されます。たとえば、室温の金属線を熱湯に浸すとエネルギーが金属線へと伝達されます(線が熱湯から熱を吸収します)。または、あなたが金属線を素早く前後に曲げるとエネルギーが金属線へと伝達されます(線に仕事がされたため温かくなります)。どちらも線の内部エネルギーを増加させ、それが線の温度上昇に反映されます。逆に、系から熱が失われたり、系が周囲に仕事をしたりすると、エネルギーが系の外へと伝達されます。
内部エネルギー、熱、仕事の間の関係性は、図5.19に示されるように、この方程式によって表すことができます:
\[ ΔU = q + w \]
これは熱力学の第一法則の1つのバージョンであり、系の内部エネルギーは、系に入ったり出たりする熱流を通じて変化すること(正のqは熱の流れ込み、負のqは熱の流れ出し)、または系に対してなされたり系によって行われたりした仕事を通じて変化することを示しています。仕事wは、系に対してなされた場合は正であり、系によって行われた場合は負です。
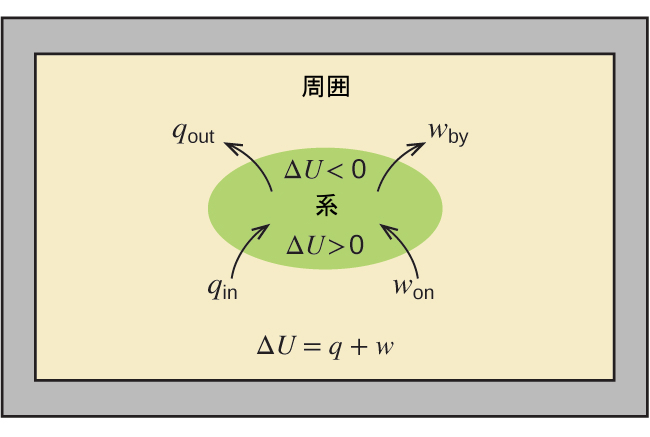
図5.19 | 系の内部エネルギーUは、熱流と仕事によって変化します。もし熱が系に流入した場合(qin)、または系に対して仕事がなされた場合(won)、系の内部エネルギーは増加します(ΔU > 0)。もし熱が系から流出した場合(qout)、または系によって仕事が行われた場合(wby)、その内部エネルギーは減少します(ΔU < 0)。
膨張仕事(または圧力-体積仕事)と呼ばれる仕事の一種は、系が拘束するような圧力に対抗して周囲を押し戻すとき、または周囲が系を圧縮するときに発生します。これの一例は、内燃機関の動作中に発生します。ガソリンと酸素の反応は発熱性です。このエネルギーの一部は熱として放出され、一部はシリンダー内のピストンを押す仕事をします。反応に関与する物質が系であり、エンジンと残りの宇宙全体がその周囲です。系は、加熱することと周囲に仕事をすることの両方によってエネルギーを失い、その内部エネルギーは減少します。(エンジンが動いている間は、このプロセスが1秒間に何度も繰り返されているため、エンジンは車を動かし続けることができます。)私たちは、熱力学の章において、化学的または物理的変化に伴う仕事の量の求め方を検討します。
学習へのリンク
この内燃機関の見取り図(http://openstaxcollege.org/l/16combustion)は、ガソリンなどの燃料の発熱燃焼反応によって生じるエネルギーが運動エネルギーに変換される様子を示しています。
これまで議論してきたように、内部エネルギー、熱、仕事の間の関係性は、ΔU = q + w のように表すことができます。内部エネルギーは状態関数(または状態変数)の一例ですが、熱や仕事は状態関数ではありません。状態関数の値は、系がある状態にのみ依存し、その状態にどのようにして到達したかには依存しません。もしある量が状態関数でない場合、その値はその状態にどのように到達するかに依存します。状態関数の例としては、高度または標高があります。もしあなたがキリマンジャロ山の山頂に立っている場合、あなたは標高5895mにおり、そこに歩いて登ったかパラシュートで降り立ったかは関係ありません。しかしながら、キリマンジャロの頂上までの移動距離は状態関数ではありません。あなたは、キリマンジャロの頂上まで直行ルートで登ることもできますし、もっと遠回りの曲がりくねった道で登ることもできます(図5.20)。移動した距離は異なるでしょうが(距離は状態関数ではありません)、到達した標高は同じです(標高は状態関数です)。
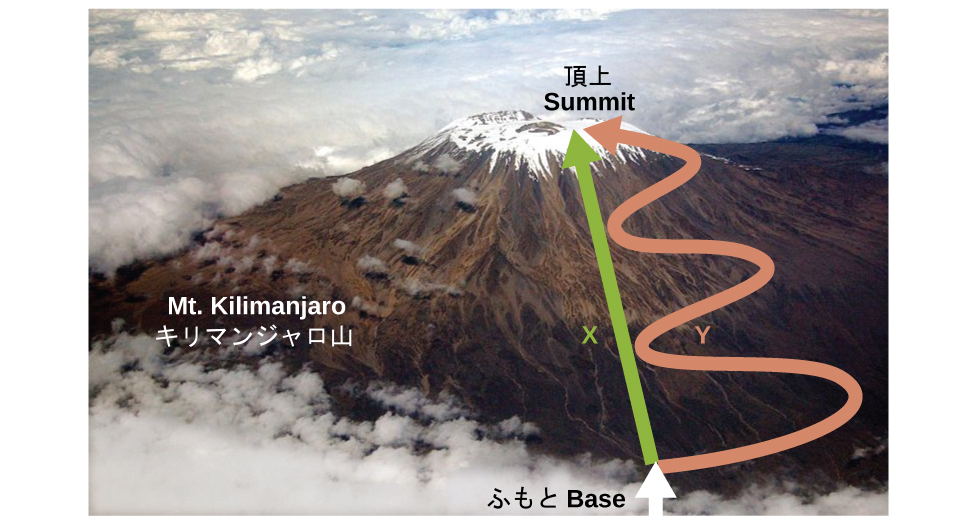
図5.20 | XとYはキリマンジャロ山頂までの2つの異なるルートを表しています。どちらも高度の変化は同じですが(山の高度や標高は状態関数であり、経路には依存しません)、移動距離は大きく異なります(歩いた距離は状態関数ではなく、経路に依存します)。(credit: modification of work by Paul Shaffner)
化学者は通常、化学的および物理的プロセスの熱力学を記述するためにエンタルピー(H)として知られている性質を使います。エンタルピーは、系の内部エネルギー(U)と、系の圧力(P)および体積(V)の数学的積との和として定義されます:
\[ H = U + PV \]
エンタルピーも状態関数です。特定の物質のエンタルピー値を直接測定することはできません。化学的または物理的プロセスのエンタルピー変化のみを決定することができます。定圧で行われるプロセス(多くの化学的および物理的変化に共通の条件)では、エンタルピーの変化(ΔH)は以下のようになります:
\[ ΔH = ΔU + PΔV \]
数学的な積PΔVは、仕事(w)、すなわち、膨張仕事または圧力-体積仕事を表しています。それらの定義により、ΔVとwの算術符号は常に反対になります:
\[ PΔV = −w \]
この式と内部エネルギーの定義をエンタルピー変化の式に代入すると、以下のようになります:
\[ \begin{array}{ll} ΔH = ΔU + PΔV\\ = q_p + w − w\\ = q_p \end{array} \]
ここでqpは定圧条件下での反応の熱です。
このように、もし化学的および物理的なプロセスが一定圧力下で行われ、膨張または収縮によって引き起こされる仕事のみがなされている場合、そのプロセスの熱流(qp)とエンタルピー変化(ΔH)は等しくなります。
ブンゼンバーナーを作動させたときに放出される熱は、そこで行われるメタンの燃焼反応のエンタルピー変化と等しくなります。なぜなら、メタンの燃焼反応が大気圧という実質的に一定の圧力下で発生するからです。一方、ボンベ熱量計(図5.17)の中で測定される反応で発生する熱は、ΔHとは等しくありません。なぜなら、密閉された一定体積の金属容器では圧力が一定のままであることができないからです(反応で得られるガス種の量が増えたり減ったりすると、圧力が増減することがあります)。化学者は通常、一般的な大気圧の条件下で、一定の外圧でq = ΔHとして実験を行うので、化学反応の熱変化を決定するための最も便利な選択肢はエンタルピーとなります。
ΔHを使用する際には、以下の規則が適用されます:
• エンタルピーの変化の負の値(ΔH < 0)は発熱反応を示し、正の値(ΔH > 0)は吸熱反応を示します。化学反応式の方向が逆になると、そのΔHの算術符号が変化します(一方の方向では吸熱性のプロセスであったものが、他方の方向では発熱性のプロセスになります)。
• 化学者は熱化学方程式を使って物質とエネルギーの変化を表現します。熱化学方程式では、反応のエンタルピーの変化は、反応の式に従ってΔHの値として示されます。このΔHの値は、化学反応式に示されるモル数の反応物と生成物が含まれる反応に関連する熱の量を示しています。たとえば、この反応式を考えてみましょう:
\[ {\rm H_2\ (g) +\frac{1}{2} O_2\ (g) ⟶ H_2 O\ (l)} \hspace{20pt} ΔH = −286\rm \ kJ \]
この反応式は、ある温度と圧力にある1モルの水素気体と1/2モルの酸素気体が、同じ温度と圧力にある液体の水1モルに変化するとき、286kJの熱が周囲に放出されることを示しています。もしこの化学反応式の係数に何らかの数を掛けるならば、エンタルピーの変化にもその同じ数を掛けなければなりません(ΔHは示量性です):
\[ \begin{array}{ll} (量が2倍に増加)\\ {\rm 2H_2\ (g) + O_2\ (g) ⟶ 2H_2 O\ (l)} \hspace{20pt} ΔH = {\rm 2 × (−286\ kJ) = −572\ kJ}\\ (量が半分に減少)\\ {\rm \frac{1}{2} H_2\ (g) +\frac{1}{4} O_2\ (g) ⟶\frac{1}{2} H_2 O\ (l)} \hspace{20pt} ΔH ={\rm \frac{1}{2}× (−286\ kJ) = −143\ kJ} \end{array} \]
• 反応のエンタルピー変化は、反応物と生成物の物理状態に依存するので、これらを示さなければなりません。たとえば、1モルの水素気体と1/2モルの酸素気体が、同じ温度と圧力にある液体の水1モルに変化するときには、286kJの熱が放出されます。気体の水が形成される場合は、242kJの熱しか放出されません。
\[ {\rm H_2\ (g) +\frac{1}{2}O_2\ (g) ⟶ H_2 O\ (g)} \hspace{20pt} ΔH = \rm −242\ kJ \]
例題5.8 熱化学方程式を書く
0.0500モルのHCl(aq)が0.0500モルのNaOH(aq)と反応して0.0500モルのNaCl(aq)を生成するとき、2.9 kJの熱が発生しました。1モルのHClの反応についてのバランスの取れた熱化学方程式を書いてください。
\[ {\rm HCl\ (aq) + NaOH\ (aq) ⟶ NaCl\ (aq) + H_2 O\ (l)} \]
解法
0.0500モルの酸(HCl)の反応の場合、q = -2.9 kJです。反応物は化学量論的な量(バランスの取れた反応式と同じモル比)で提供されているので、酸の量は、モルエンタルピーの変化を計算するために使用することができます。ΔHは示量性なので、それは中和される酸の量に比例します:
\[ ΔH =\rm 1\ mol\ HCl ×\frac{−2.9\ kJ}{0.0500\ mol\ HCl}= −58\ kJ \]
そして、熱化学方程式は
\[ {\rm HCl\ (aq) + NaOH\ (aq) ⟶ NaCl\ (aq) + H_2 O\ (l)} \hspace{20pt} ΔH = \rm −58\ kJ \]
学習内容の確認
1.34gのZn(s)を0.750MのHCl(aq)60.0 mLと反応させると、3.14 kJ の熱が発生します。以下の反応について、反応する亜鉛1モルあたりのエンタルピー変化を決定してください:
\[ \rm Zn\ (s) + 2HCl\ (aq) ⟶ ZnCl_2\ (aq) + H_2\ (g) \]
解答:ΔH = −153 kJ
化学反応のΔHを決定する際には、化学量論と限定反応物の両方を確実に考慮に入れるようにしてください。
例題5.9 熱化学方程式を書く
お菓子のグミに2.67 g のスクロース(C₁₂H₂₂O₁₁)が含まれています。これを 7.19 g の塩素酸カリウム(KClO₃)と反応させると、43.7 kJ の熱が発生しました。1モルのスクロースの反応についての熱化学方程式を書いてください:
\[ \rm C_{12} H_{22} O_{11}\ (aq) + 8KClO_3\ (aq) ⟶ 12CO_2\ (g) + 11H_2 O\ (l) + 8KCl\ (aq) \]
解法
前の例題とは異なり、この例題では化学量論的な量の反応物を反応させていないので、限定反応物(これが反応で得られるものと、生成または消費される熱エネルギーの量とを制限します)を特定しなければなりません。
2つの反応物の与えられた量は以下の通りです:
\[ \rm (2.67\ g)(1\ mol/342.3\ g)= 0.00780\ mol\ C_{12} H_{22}O_{11}\\ (7.19\ g)(1\ mol/122.5\ g)= 0.0587\ mol\ KClO_3 \]
与えられた塩素酸とスクロースのモル比は以下の通りです:
\[ \rm 0.0587\ mol\ KClO_3 /0.00780\ mol\ C_{12} H_{22} O_{11} = 7.52 \]
バランスの取れた反応式は、1molのC₁₂H₂₂O₁₁との反応に8molのKClO₃が必要であることを示しています。与えられた量のKClO₃は化学量論的な量よりも少ないので、それは限定反応物であり、エンタルピーの変化を計算するために使用することができます:
\[ ΔH = \rm -43.7\ kJ/0.0587\ mol\ KClO_3 = 744\ kJ/mol\ KClO_3 \]
この反応式は、書かれているように、8molのKClO₃の反応を表しているので、エンタルピーの変化は以下のようになります:
\[ \rm (744\ kJ/mol\ KClO_3)(8\ mol\ KClO_3) = 5960\ kJ \]
この反応のエンタルピー変化は-5960kJであり、熱化学方程式は以下の通りです:
\[ {\rm C_{12} H_{22} O_{11} + 8KClO_3 ⟶ 12CO_2 + 11H_2 O + 8KCl} \hspace{20pt} ΔH =\rm −5960\ kJ \]
学習内容の確認
1.42 g の鉄と 1.80 g の塩素を反応させると、3.22 g の FeCl₂(s) と 8.60 kJ の熱が発生しました。1モルのFeCl₂(s)が生成されたときの反応のエンタルピー変化は何ですか?
解答:ΔH = −338 kJ
エンタルピーの変化は、通常、反応物と生成物の両方が同じ条件にある反応について一覧にされています。標準状態とは、他の異なる条件下での性質を決定するための参照点として使用される一般的に受け入れられている条件のセットです。化学者にとって、IUPACの標準状態とは、1barの圧力下の物質と1Mの溶液のことを指し、温度は指定されていません。多くの熱化学の表では、1atmの標準状態の値が記載されています。圧力の小さな変化(1 bar = 0.987 atm)では反応のΔHはほとんど変化しないので、ΔHの値(最も正確に測定された値を除く)は、両方の標準状態のセットの下で基本的に同じです。私たちは、標準状態を指定するために、エンタルピー変化の記号に上付きの「o」を含めることにします。通常の(厳密には標準ではありません)温度は298.15 Kなので、他の温度が指定されない限り、この温度が想定されます。したがって、これらの条件下で発生するプロセスのエンタルピー変化を示すために、記号(ΔH°)が使用されます。(ΔHという記号は、非標準条件下で起こる反応についてのエンタルピー変化を示すために使用されます。)
多くの種類の化学的および物理的プロセスのエンタルピー変化は、参考文献(燃焼反応、相転移、生成反応についてのものを含む)の中で入手可能です。これらの量を議論するとき、エンタルピーとエンタルピー変化の示量性という性質に注意を払うことが重要です。所与の反応のエンタルピー変化は、関与する物質の量に比例するので、エンタルピー変化はそれに基づいて報告されることがあるかもしれません(すなわち、特定の量の反応物のΔHとして)。しかしながら、ある示量性(ΔH)を別の示量性(物質の量)で割って、量あたりのΔHという示強性の値(しばしば1モルあたりで「正規化」されています)を報告するのがより有用であることに気づくことがよくあります。(これは、前に見たように、示量性の熱容量から示強性の比熱を決定するのと似ていることに注意してください。)
標準燃焼エンタルピー
標準燃焼エンタルピー(ΔHc°)は、1モルの物質が標準状態の条件下で燃焼(酸素と激しく結合)したときのエンタルピーの変化であり、「燃焼熱」と呼ばれることもあります。たとえば、エタノールの燃焼エンタルピー(-1366.8 kJ/mol)は、1モルのエタノールが25 °Cと1気圧で完全燃焼し、やはり25 °Cと1atmで生成物が得られるときに生成される熱の量です。
\[ {\rm C_2 H_5 OH\ (l) + 3O_2\ (g) ⟶ 2CO_2 + 3H_2 O\ (l)} \hspace{20pt} ΔH° = {\rm −1366.8\ kJ} \]
多くの物質の燃焼エンタルピーが測定されています。そのうちのいくつかが表5.2に列挙されています。水素、炭素(石炭や炭など)、およびメタン、プロパン、ガソリンの主要成分などの炭化水素(水素と炭素のみを含む化合物)などといった、燃焼エンタルピーが大きく容易に入手可能な物質の多くが燃料として使用されています。
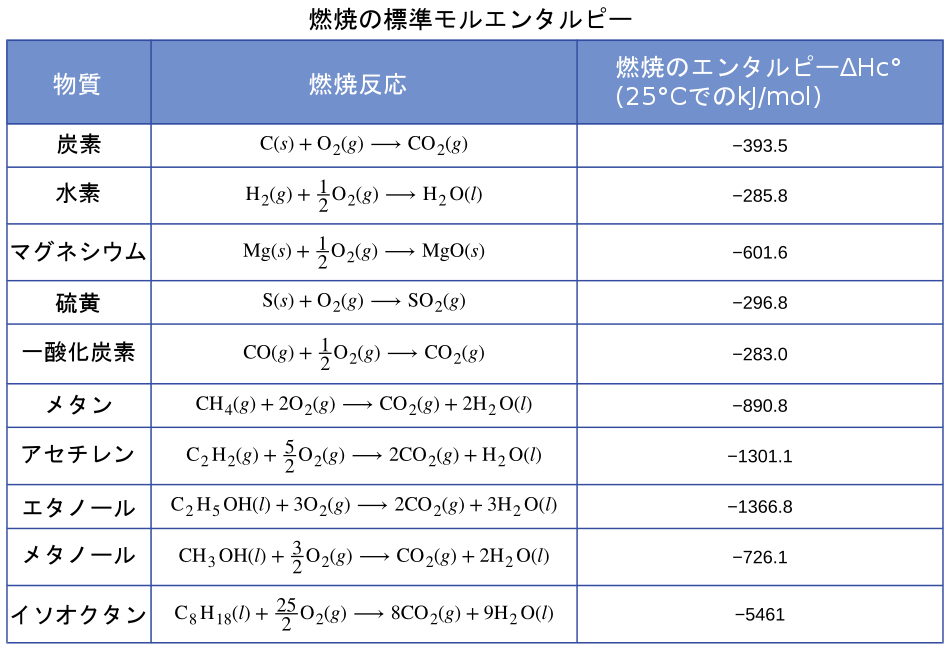
表5.2
例題5.10 燃焼のエンタルピーを利用する
図5.21が示すように、ガソリンの燃焼は非常に発熱性の高いプロセスです。ガソリンの燃焼のエンタルピーがガソリンの一般的な成分であるイソオクタンの燃焼のエンタルピーと同じであると仮定して、1.00Lのガソリンを燃焼させることによって発生する熱のおおよその量を求めてみましょう。イソオクタンの密度は0.692g/mLです。

図5.21 | ガソリンの燃焼は非常に発熱性が高いです。(credit: modification of work by “AlexEagle”/Flickr)
解法
既知の量(1.00 Lのイソオクタン)から始めて、所望の熱の量またはエネルギーに到達するまで、単位間の変換を行うことができます。イソオクタンの燃焼エンタルピーは、必要な変換の1つを提供してくれます。表5.2はこの値を1モルのイソオクタン(C₈H₁₈)あたり-5460 kJとしています。
これらのデータを使用すると
\[ \begin{array}{ll} \rm 1.00\ L\ C_8 H_{18} ×\frac{1000\ mL\ C_8 H_{18}}{1\ L\ C_8 H_{18}}×\frac{0.692\ g\ C_8 H_{18}}{1\ mL\ C_8 H_{18}}×\frac{1\ mol\ C_8 H_{18}}{114\ g\ C_8 H_{18}}×\frac{−5460\ kJ}{1\ mol\ C_8 H_{18}}\\ \rm = −3.31× 10^4\ kJ \end{array} \]
1.00 Lのイソオクタンを燃焼させると33100 kJの熱が発生します。(このエネルギーの量は、99.2kg(約218ポンド)の氷を溶かすのに十分な量です。)
注:もしあなたがこの計算を一度に一段階ずつ行うならば、以下のようになります:
\[ \rm 1.00\ L\ C_8 H_{18} ⟶ 1.00 × 10^3\ mL\ C_8 H_{18}\\ 1.00 × 10^3\ mL\ C_8 H_{18} ⟶ 692\ g\ C_8 H_{18}\\ 692\ g\ C_8 H_{18} ⟶ 6.07\ mol\ C_8 H_{18}\\ 6.07\ mol\ C_8 H_{18} ⟶ −3.31× 10^4\ kJ \]
学習内容の確認
125gのアセチレンを燃焼させることによってどれだけの量の熱が発生するでしょうか?
解答:6.25 × 10³kJ
日常生活の中の化学
藻類を利用した新しいエネルギー技術(バイオ燃料)
化石燃料の埋蔵量が減少し、抽出コストが上昇する中、将来の代替燃料源の探索が進められています。最も有望なバイオ燃料は藻類由来のものです(図5.22)。使用される藻類の種は無毒で生分解性であり、世界で最も急速に成長する生物の1つです。藻類の重量の約50%は油分であり、その油分はバイオディーゼルなどの燃料に容易に変換できます。藻類は、1ヘクタールあたり2万6000ガロンのバイオ燃料を生産することができ、他の作物よりも1エーカーあたりのエネルギー量が多いです。藻類の中には、他の作物の栽培には使えない汽水域でも繁殖できるものもあります。藻類は、バイオディーゼル、バイオガソリン、エタノール、ブタノール、メタン、ジェット燃料さえも生産することができます。

図5.22 | (a)小さな藻類は、(b)大きな量へと生育し、最終的には(c)バイオディーゼルなどの有用な燃料にすることができます。(credit a: modification of work by Micah Sittig; credit b: modification of work by Robert Kerton; credit c: modification of work by John F. Williams)
米国エネルギー省によると、わずか3万9000平方キロメートル(米国の国土の約0.4%、またはトウモロコシの栽培に使用されている面積の1/7以下)の面積で、米国内で使用されているすべての石油系燃料を置き換えるのに十分な藻類燃料を生産することができます。藻類燃料のコストは競争力を増しています - たとえば、アメリカ空軍は1ガロンあたり5ドル以下の総コストで藻類からジェット燃料を生産しています。[3]藻類燃料の製造に利用されるプロセスは以下の通りです:藻類(太陽光をエネルギー源とし、CO₂を原料とします)を生育させ、藻類を収穫し、燃料化合物(または前駆体化合物)を抽出し、必要に応じて加工し(たとえば、バイオディーゼルを製造するためにエステル交換反応を行い)、精製し、流通させます(図5.23)。
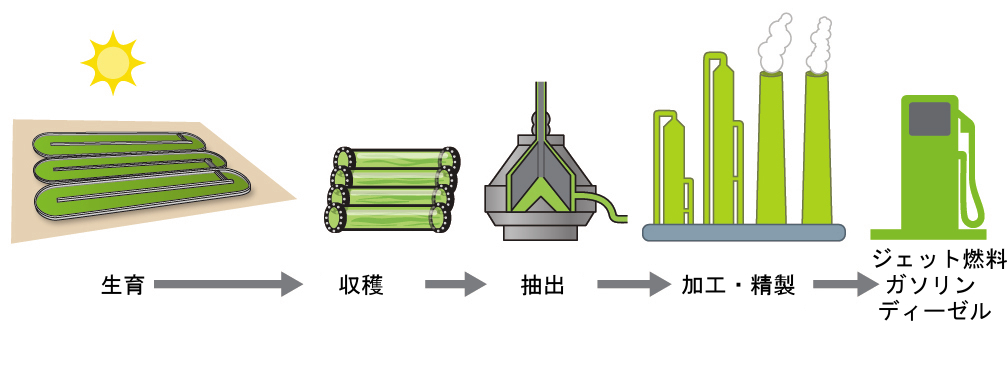
図5.23 | 藻類は太陽光と二酸化炭素を油に変換し、その油は収穫、抽出、精製されてさまざまな再生可能燃料へと変換されます。
学習へのリンク
藻類バイオ燃料の生成過程についてより詳しく学ぶためには、こちら(http://openstaxcollege.org/l/16biofuel)をクリックしてください。
標準生成エンタルピー
標準生成エンタルピーΔHf°とは、標準状態の条件下で、最も安定な状態にある遊離元素からちょうど1モルの純物質が生成される反応のエンタルピー変化のことです。これらの値は、実行することが非現実的であったり危険であったりする化学反応や、測定が困難なプロセスのエンタルピー変化を計算したり、予測したりするのに特に有用です。もし私たちが適切な標準生成エンタルピーの値を持っているならば、私たちはあらゆる反応のエンタルピー変化を求めることができます(私たちは次のヘスの法則に関する項で練習します)。
CO₂(g)の標準生成エンタルピーは-393.5 kJ/molです。これは発熱反応のエンタルピー変化です:
\[ {\rm C\ (s) + O_2\ (g) ⟶ CO_2\ (g)} \hspace{20pt} ΔH_{\rm f} ° = ΔH° = {\rm −393.5\ kJ} \]
1atmの圧力、25°Cにある反応物から開始し(この条件下で最も安定した炭素の形態である黒鉛として炭素が存在している状態で)、同じく1atm、25°Cにある1モルのCO₂でもって終了します。二酸化窒素NO₂(g)の場合、ΔHf°は33.2 kJ/molです。これは吸熱反応のエンタルピー変化です:
\[ {\rm \frac{1}{2} N_2\ (g) + O_2\ (g) ⟶ NO_2\ (g)} \hspace{20pt} ΔH_{\rm f} ° = ΔH° = {\rm +33.2\ kJ} \]
この場合では、1/2モルのN₂と1モルのO₂という反応式が、正しいです。なぜなら、標準生成エンタルピーは常に1モルの生成物NO₂(g)を参照しているからです。
多くの一般的な物質についての標準生成エンタルピーの表が付録Gにあります。これらの値は、非常に発熱性の高いもの(P₄O₁₀の生成についての-2984 kJ/mol のような)から強い吸熱性のもの(アセチレンC₂H₂の生成についての+226.7 kJ/mol のような)に至るまでの範囲の生成反応を示しています。定義により、最も安定的な形態の元素の標準生成エンタルピーは、標準的な条件下(気体では1atm、溶液では1M)ではゼロに等しくなります。
例題5.11 生成エンタルピーの値を求める
オゾンO₃(g)は酸素O₂(g)から吸熱過程によって生成されます。紫外線放射は、上層大気でこの反応を引き起こすエネルギー源です。反応の反応物と生成物の両方が標準状態にあると仮定して、以下の情報からオゾンの標準生成エンタルピーΔHf°を決定してください:
\[ {\rm 3O_2\ (g) ⟶ 2O_3\ (g)} \hspace{20pt} ΔH° = {\rm +286\ kJ} \]
解法
ΔHf°は、標準状態にある元素から、標準状態にある1モルの物質を形成するときのエンタルピー変化です。したがって、O₃(g)のΔHf°は、以下の反応についてのエンタルピー変化です:
\[ \rm \frac{3}{2} O_2\ (g) ⟶ O_3\ (g) \]
2 molのO₃(g)の生成については、ΔH°= +286 kJです。この比(286 kJ/2 mol O₃)は、1モルのO₃(g)が形成されたときに生成される熱(これがO₃(g)の生成エンタルピーです)を求めるための変換係数として使用することができます:
\[ 1モルの{\rm O_3\ (g)}についてのΔH° = \rm 1\ mol\ O_3 ×\frac{286\ kJ}{2\ mol\ O_3}= 143 kJ \]
したがって、ΔHf° [O₃(g)] = +143 kJ/molとなります。
学習内容の確認
水素気体H₂は、気体状の塩素Cl₂と爆発的に反応して塩化水素HCl(g)を生成します。反応物と生成物の両方が標準状態の条件にある場合、1モルのH₂(g)と1モルのCl₂(g)の反応についてのエンタルピーの変化は何ですか?HCl(g)の標準生成エンタルピーは-92.3 kJ/molです。
解答:H₂(g) + Cl₂(g) ⟶ 2HCl(g)の反応について、ΔH° = −184.6kJ。
例題5.12 ΔHf°のための反応方程式を書く
以下について、生成熱のための反応方程式を書いてください:
(a)C₂H₅OH(l)
(b)Ca₃(PO₄)₂(s)
解法
ΔHf°反応方程式は、標準的な条件下で、構成要素の元素から1モルの化合物を形成するためのものであることを思い出すと、私たちは以下を得ます:
\[ \rm (a)\ 2C(s,黒鉛) + 3H_2\ (g) +\frac{1}{2} O_2\ (g) ⟶ C_2 H_5 OH\ (l)\\ (b)\ 3Ca\ (s) +\frac{1}{2} P_4\ (s) + 4O_2\ (g) ⟶ Ca_3 (PO_4 )_2\ (s) \]
注:炭素の標準状態は黒鉛であり、リンはP₄として存在しています。
学習内容の確認
以下について、生成熱のための反応方程式を書いてください:
(a)C₂H₅OC₂H₅(l)
(b)Na₂CO₃(s)
解答: \[ \rm (a)\ 4C\ (s,黒鉛) + 5H_2\ (g) +\frac{1}{2} O_2\ (g) ⟶ C_2 H_5 OC_2 H_5\ (l)\\ (b)\ 2Na\ (s) + C\ (s,黒鉛) +\frac{3}{2} O_2\ (g) ⟶ Na_2 CO_3\ (s) \]
ヘスの法則
化学的変化に関与する熱の量を決定するためには、2つの方法があります:実験的に測定する方法と、実験的に決定された他のエンタルピー変化から計算する方法です。いくつかの反応は、実験的に調べて、正確な測定を行うことが(不可能ではないにしても)難しいです。また、反応の実行や測定が難しくない場合でも、実験を行わずに反応に関与する熱を求めることができれば便利です。
この種の計算では、通常、ヘスの法則を利用します。ヘスの法則は以下のことを述べています:もしあるプロセスがいくつかの段階的なプロセスの総和として書くことができる場合、プロセス全体のエンタルピー変化は、さまざまな段階のエンタルピー変化の総和に等しくなります。エンタルピーが状態関数であるため、ヘスの法則が成り立ちます:エンタルピーの変化は、化学プロセスがどこで始まり、どこで終わるかにのみ依存しますが、開始から終了までの経路には依存しません。たとえば、炭素と酸素から二酸化炭素が生成する反応は、直接的なプロセスまたは2段階のプロセスのいずれかによって起こると考えることができます。直接的な反応は以下のように書かれます:
\[ {\rm C\ (s) + O_2\ (g) ⟶ CO_2\ (g)} \hspace{20pt} ΔH° = {\rm −394\ kJ} \]
二段階のプロセスでは、まず一酸化炭素が生成されます:
\[ {\rm C\ (s) +\frac{1}{2} O_2\ (g) ⟶ CO\ (g)} \hspace{20pt} ΔH° = {\rm −111\ kJ} \]
次に、一酸化炭素はさらに反応して二酸化炭素を生成します:
\[ {\rm CO\ (g) +\frac{1}{2} O_2\ (g) ⟶ CO_2\ (g)} \hspace{20pt} ΔH° = {\rm −283\ kJ} \]
全体の反応を記述する反応式は、これら2つの化学的変化の合計です:
\[ \begin{array}{ll} ステップ1:{\rm C\ (s) +\frac{1}{2} O_2\ (g) ⟶ CO\ (g)}\\ ステップ2:{\rm CO\ (g) +\frac{1}{2} O_2\ (g) ⟶ CO_2\ (g)}\\ \hline 合計:{\rm C\ (s) +\frac{1}{2} O_2\ (g) + CO\ (g) +\frac{1}{2} O_2\ (g)⟶ CO\ (g) + CO_2\ (g)} \end{array} \]
ステップ1で生成されたCOはステップ2で消費されるので、正味の変化は:
\[ {\rm C\ (s) + O_2\ (g) ⟶ CO_2\ (g)} \]
ヘスの法則によれば、反応のエンタルピー変化はそれぞれのステップのエンタルピー変化の合計に等しくなるでしょう。
\[ \begin{array}{ll} {\rm C\ (s) +\frac{1}{2} O_2\ (g) ⟶ CO\ (g)} \hspace{33pt} ΔH° = {\rm −111\ kJ}\\ {\rm CO\ (g) +\frac{1}{2} O_2\ (g) ⟶ CO_2\ (g)} \hspace{20pt} ΔH° = {\rm −283\ kJ}\\ \hline {\rm C\ (s) + O_2\ (g) ⟶ CO_2\ (g)} \hspace{37pt} ΔH° = {\rm −394\ kJ}\\ \end{array} \]
この結果が図5.24に示されています。反応が1つのステップで起こったとしても2つのステップで起こったとしても、反応全体のΔHは同じであることが見て取れます。この結果(反応全体のΔH=反応全体の中における反応の「ステップ」のΔHの値の総和)は、化学的および物理的プロセス全般に当てはまります。
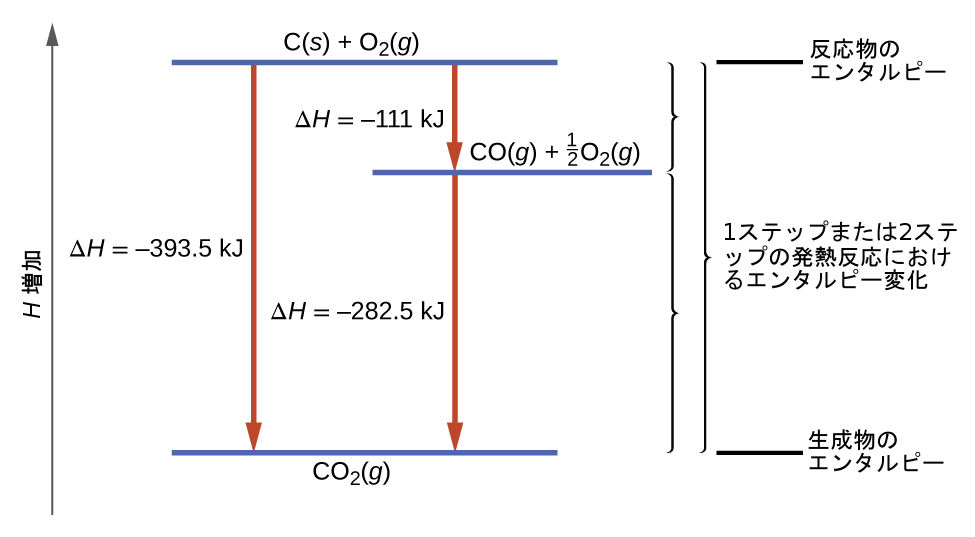
図5.24 | 元素からのCO₂(g)の生成は、2つのステップで起こると考えることができます。それらは、ヘスの法則で記述されているように、足し合わせて全体の反応にすることができます。青色の水平線はエンタルピーを表しています。発熱性のプロセスでは、生成物は反応物よりも低いエンタルピーになります。
ヘスの法則を使ってさらに練習する前に、ΔHの2つの重要な特徴を思い出してみましょう。
ΔHは反応物または生成物の量に正比例します。たとえば、1モルのNO₂(g)を生成する反応のエンタルピー変化は+33.2kJです:
\[ {\rm \frac{1}{2} N_2\ (g) + O_2\ (g) ⟶ NO_2\ (g)} \hspace{20pt} ΔH = {\rm +33.2\ kJ} \] 2モルのNO₂(2倍)が生成されるとき、ΔHは2倍になります:
\[ {\rm N_2\ (g) + 2O_2\ (g) ⟶ 2NO_2\ (g)} \hspace{20pt} ΔH = {\rm +66.4\ kJ} \] 一般的に、もし私たちが反応式に数を掛けたり割ったりする場合には、エンタルピーの変化にも同じ数を掛けたり割ったりします。一方向の反応のΔHは、逆方向の反応のΔHと大きさが等しく、符号が逆になります。たとえば、以下のものが与えられたとします:
\[ {\rm H_2\ (g) + Cl_2\ (g) ⟶ 2HCl\ (g)} \hspace{20pt} ΔH = {\rm −184.6\ kJ} \] 次に、「逆」の反応については、エンタルピーの変化も「逆」になります:
\[ {\rm 2HCl\ (g) ⟶ H_2\ (g) + Cl_2\ (g)} \hspace{20pt} ΔH = {\rm +184.6\ kJ} \]
例題5.13 ヘスの法則を用いたΔHf°の段階的な計算
標準状態の条件下で発生する以下の2段階のプロセスのエンタルピーの変化から、FeCl₃(s)の生成エンタルピーΔHf°を決定してください:
\[ {\rm Fe\ (s) + Cl_2\ (g) ⟶ FeCl_2\ (s)} \hspace{20pt} ΔH° = {\rm −341.8\ kJ}\\ {\rm FeCl_2\ (s) +\frac{1}{2} Cl_2\ (g) ⟶ FeCl_3 (s)} \hspace{20pt} ΔH° = {\rm −57.7\ kJ} \]
解法
私たちはFeCl₃(s)の標準生成エンタルピーを求めようとしていますが、それはこの反応についてのΔH°に等しいです:
\[ {\rm Fe\ (s) +\frac{3}{2} Cl_2\ (g) ⟶ FeCl_3\ (s)} \hspace{20pt} ΔH_{\rm f} ° = ? \]
反応を見てみると、私たちがΔH°を求めたい反応は、既知のΔHの値を持つ2つの反応の合計であることがわかりますので、それらのΔHを合計しなければなりません:
\[ \begin{array}{ll} {\rm Fe\ (s) + Cl_2\ (g) ⟶ FeCl_2\ (s)} \hspace{42pt} ΔH° = {\rm −341.8\ kJ}\\ {\rm FeCl_2\ (s) +\frac{1}{2} Cl_2\ (g) ⟶ FeCl_3\ (s)} \hspace{20pt} ΔH° = {\rm −57.7\ kJ}\\ \hline {\rm Fe\ (s) +\frac{3}{2} Cl_2\ (g) ⟶ FeCl_3\ (s)} \hspace{35pt} ΔH° = {\rm −399.5\ kJ}\\ \end{array} \]
FeCl₃(s)の生成エンタルピーΔHf°は-399.5 kJ/molです。
学習内容の確認
このプロセスのΔHを計算してください:
\[ {\rm N_2\ (g) + 2O_2\ (g) ⟶ 2NO_2\ (g)} \]
以下の情報を用いてください:
\[ {\rm N_2\ (g) + O_2\ (g) ⟶ 2NO\ (g)} \hspace{20pt} ΔH = {\rm 180.5\ kJ}\\ {\rm NO\ (g) +\frac{1}{2} O_2\ (g) ⟶ NO_2\ (g)} \hspace{20pt} ΔH = {\rm −57.06\ kJ} \]
解答:66.4 kJ
次のものは、多くのヘスの法則の問題を解く際に関連する思考プロセスを説明する、それほど単純ではない例です。これは、実験的に決定するのが困難な場合に、多くの標準生成エンタルピー(およびΔHの他の値)を見つけることができる方法を示しています。
例題5.14 ヘスの法則を用いたさらに難しい問題
一フッ化塩素はフッ素と反応して三フッ化塩素を形成することができます:
\[ (i)\ {\rm ClF\ (g) + F_2\ (g) ⟶ ClF_3\ (g)} \hspace{20pt} ΔH° = ? \]
これらの反応を用いて、反応(i)のΔH°を求めてください:
\[ \begin{array}{ll} (ii)\ {\rm 2OF_2\ (g) ⟶ O_2\ (g) + 2F_2\ (g)} \hspace{20pt} ΔH_{(ii)} ° = {\rm −49.4\ kJ}\\ (iii)\ {\rm 2ClF\ (g) + O_2\ (g) ⟶ Cl_2 O\ (g) + OF_2\ (g)} \hspace{20pt} ΔH_{(iii)} ° = {\rm +214.0\ kJ}\\ (iv)\ {\rm ClF_3\ (g) + O_2\ (g) ⟶ \frac{1}{2} Cl_2 O\ (g) +\frac{3}{2} OF_2\ (g)} \hspace{20pt} ΔH_{(iv)} ° = {\rm +236.2\ kJ} \end{array} \]
解法
私たちの目標は、(ii)、(iii)、(iv)の反応を操作して組み合わせて、(i)の反応になるようにすることです。(i)の左から右に向かうと、私たちはまず、反応物としてClF(g)が必要であることがわかります。これは反応(iii)に1/2を掛けることによって得ることができます。それは、ΔH°の変化にも1/2を掛けることを意味します:
\[ {\rm ClF\ (g) +\frac{1}{2} O_2\ (g) ⟶\frac{1}{2} Cl_2 O\ (g) +\frac{1}{2} OF_2\ (g)} \hspace{20pt} ΔH° ={\rm \frac{1}{2} (214.0) = +107.0\ kJ} \]
次に、反応物としてF₂も必要であることがわかります。これを得るには、反応(ii)を逆にして、半分にします。これは、ΔH°の符号を変えて半分にすることを意味します:
\[ {\rm \frac{1}{2} O_2\ (g) + F_2\ (g) ⟶ OF_2\ (g)} \hspace{20pt} ΔH° = {\rm +24.7\ kJ} \]
生成物としてClF₃を得るには、(iv)を逆にしてΔH°の符号を変えます:
\[ {\rm \frac{1}{2} Cl_2 O\ (g) +\frac{3}{2} OF_2\ (g) ⟶ ClF_3\ (g) + O_2\ (g)} \hspace{20pt} ΔH° = {\rm −236.2\ kJ} \]
それでは、これらの反応を足し合わせて私たちが求める反応となることを確認してください:
\[ \begin{array}{ll} {\rm ClF\ (g) +\frac{1}{2} O_2\ (g) ⟶\frac{1}{2} Cl_2 O\ (g) +\frac{1}{2} OF_2\ (g)} \hspace{20pt} ΔH° = {\rm +107.0\ kJ}\\ {\rm \frac{1}{2} O_2\ (g) + F_2\ (g) ⟶ OF_2\ (g)} \hspace{90pt} ΔH° = {\rm +24.7\ kJ}\\ {\rm \frac{1}{2} Cl_2 O\ (g) +\frac{3}{2} OF_2\ (g) ⟶ ClF_3\ (g) + O_2\ (g)} \hspace{23pt} ΔH° = {\rm −236.2\ kJ}\\ \hline {\rm ClF\ (g) + F_2\ (g) ⟶ ClF_3\ (g)} \hspace{90pt} ΔH° = {\rm −104.5\ kJ}\\ \end{array} \]
反応物(1/2)O₂と(1/2)O₂は生成物O₂によって相殺され、生成物(1/2)Cl₂O は反応物(1/2)Cl₂Oによって相殺され、反応物(3/2)OF₂は生成物(1/2)OF₂とOF₂によって相殺されます。これにより反応物ClF(g)とF₂(g)、および生成物ClF₃(g)だけが残ります。これは私たちが求めるものです。これら3つの修正された反応を合計すると、目的の反応が得られるので、3つの修正されたΔH°の値を合計すると、所望のΔH°が得られます:
\[ ΔH° = {\rm (+107.0\ kJ) + (24.7\ kJ) + (−236.2\ kJ) = −104.5\ kJ} \]
学習内容の確認
塩化アルミニウムは、その元素から形成することができます:
\[ (i)\ {\rm 2Al\ (s) + 3Cl_2\ (g) ⟶ 2AlCl_3\ (s)} \hspace{20pt} ΔH° = ? \]
これらの反応を用いて、反応(i)のΔH°を求めてください:
\[ \begin{array}{ll} (ii)\ {\rm HCl\ (g) ⟶ HCl\ (aq)} \hspace{20pt} ΔH_{(ii)} ° = {\rm −74.8\ kJ}\\ (iii)\ {\rm H_2\ (g) + Cl_2\ (g) ⟶ 2HCl\ (g)} \hspace{20pt} ΔH_{(iii)} ° = {\rm −185\ kJ}\\ (iv)\ {\rm AlCl_3\ (aq) ⟶ AlCl_3\ (s)} \hspace{20pt} ΔH_{(iv)} ° = {\rm +323\ kJ/mol}\\ (v)\ {\rm 2Al\ (s) + 6HCl\ (aq) ⟶ 2AlCl_3\ (aq) + 3H_2\ (g)} \hspace{20pt} ΔH_{(v)} ° = {\rm −1049\ kJ}\\ \end{array} \]
解答:−1407 kJ
私たちはまた、任意の反応について、対応する反応物と生成物の生成エンタルピーが利用可能であれば、ヘスの法則を使用して、その反応のエンタルピー変化を決定することができます。私たちが考慮する段階的な反応は以下の通りです:(i)反応物をその成分の元素へと分解すること(エンタルピー変化は、反応物の生成エンタルピーを負の値にしたものに比例します)、その後に、(ii)生成物を作り出すために元素を再結合すること(エンタルピー変化は、生成物の生成エンタルピーに比例します)。したがって、全体の反応の標準エンタルピー変化は次のようになります:すべての生成物の標準生成エンタルピーの和(ii)に、反応物の標準生成エンタルピーを負の値にしたものの和(i)を加えたものです。これは通常、少し再配列して以下のように書くことができます。∑は「~の和」を表し、nは化学量論的な係数を表します:
\[ ΔH_{反応}° = ∑ n × ΔH_{\rm f} ° (生成物) − ∑ n × ΔH_{\rm f}° (反応物) \]
以下の例題では、なぜこの式が有効なのか、また、どのようにして関心のある反応のエンタルピー変化を計算するためにこの式を使用するかを詳しく示しています。
例題5.15 ヘスの法則を使用する
この反応の標準エンタルピー変化は何ですか?:
\[ {\rm 3NO_2\ (g) + H_2 O\ (l) ⟶ 2HNO_3\ (aq) + NO\ (g)} \hspace{20pt} ΔH° = ? \]
解法:式を使う
前で与えられたヘスの法則の特別な形と付録Gの値を使用します:
\[ \begin{array}{ll} ΔH_{反応}° = ∑ n × ΔH_{\rm f} ° (生成物) − ∑ n × ΔH_{\rm f}° (反応物)\\ \rm =\left[2\ mol\ HNO_3\ (aq) ×\frac{−206.64\ kJ}{mol\ HNO_3\ (aq)}+ 1\ mol\ NO\ (g) ×\frac{+90.25\ kJ}{mol\ NO\ (g)}\right]\\ \rm \hspace{10pt} − \left[3\ mol\ NO_2\ (g) ×\frac{+33.2\ kJ}{mol\ NO_2\ (g)}+ 1\ mol\ H_2 O\ (l) ×\frac{−285.83\ kJ}{mol\ H_2 O\ (l)}\right]\\ = [2 × (−206.64) + 90.25] − [3 × 33.2 + (−285.83)]\\ = −323.03 + 186.23\\ = \rm −136.80\ kJ \end{array} \]
解法:一般的な式が有効な理由を裏付ける
あるいは、この反応を、3NO₂(g)と1H₂O(l)を構成元素へ分解することと、それらの構成元素から2HNO₃(aq)と1NO(g)を生成することの合計として書くことができます。これらの反応を書き出し、これらの化合物のΔHf°値との関係を示す(付録Gより)と、以下のようになります:
\[ {\rm 3NO_2\ (g) ⟶ \frac{3}{2}N_2\ (g) + 3O_2\ (g)} \hspace{20pt} ΔH_1 ° = {\rm −99.6\ kJ}\\ {\rm H_2 O\ (l) ⟶ H_2\ (g) +\frac{1}{2} O_2\ (g)} \hspace{20pt} ΔH_2 ° = {\rm +285.8\ kJ}[−1× ΔH_{\rm f} °{\rm (H_2 O)}]\\ {\rm H_2\ (g) + N_2\ (g) + 3O_2\ (g) ⟶ 2HNO_3\ (aq)} \hspace{20pt} ΔH_3 ° = {\rm −414.8\ kJ}[2 × ΔH_{\rm f} °{\rm (HNO_3)}]\\ {\rm \frac{1}{2} N_2\ (g) +\frac{1}{2} O_2\ (g) ⟶ NO\ (g)} \hspace{20pt} ΔH_4 ° = {\rm +90.2\ kJ}[1 × {\rm (NO)}] \]
これらの反応式を合計すると、私たちが関心のある反応が得られます:
\[ {\rm 3NO_2\ (g) + H_2 O\ (l) ⟶ 2HNO_3\ (aq) + NO\ (g)} \]
それらのエンタルピーの変化を合計すると、私たちが求めたい値が得られます:
\[ \begin{eqnarray} ΔH_{\rm rxn} ° &=& ΔH_1 ° + ΔH_2 ° + ΔH_3 ° + ΔH_4 ° \\ &=& \rm (−99.6\ kJ) + (+285.8\ kJ) + (−414.8\ kJ) + (+90.2\ kJ)\\ &=& \rm −138.4\ kJ \end{eqnarray} \]
したがって、この反応の標準エンタルピー変化はΔH° = -138.4 kJです。
この結果は、(1)それぞれの生成物のΔHf°にその化学量論的係数を掛けて、それらの値を足し合わせ、(2)それぞれの反応物のΔHf°にその化学量論的係数を掛けて、それらの値を足し合わせ、(3)(1)の結果から(2)の結果を差し引いたものであることに注意してください。これは、上で示したように、一般的な式を使用する際の手順でもあります。
学習内容の確認
1モルのエタノールC₂H₅OH(l)が燃焼して、H₂O(l)とCO₂(g)が生成されるときの熱を計算してください。以下の生成エンタルピーを用いてください:C₂H₅OH(l)が−278 kJ/mol、H₂O(l)が−286 kJ/mol、およびCO₂(g)が−394 kJ/mol。
解答:−1368 kJ/mol
重要用語
ボンベ熱量計:一定の体積の条件下で発生するプロセスのエネルギー変化を測定するように設計された装置。一般に固体および気体の反応物または生成物を含む反応に使用される
カロリー(cal):熱やその他のエネルギーの単位。水1グラムを摂氏1度だけ上げるのに必要なエネルギーの量。1 calは4.184 Jとして定義されている
熱量計:化学的または物理的なプロセスで吸収または放出される熱の量を測定するために使用される装置
熱量測定:化学的または物理的なプロセスに関与する熱の量を測定するプロセス
化学熱力学:化学的および物理的なプロセスに関連する熱、仕事、およびすべての形態のエネルギーの間の関係性を扱う科学の領域
吸熱過程:熱を吸収する化学反応や物理的変化
エネルギー:熱を供給したり、仕事をしたりする能力
エンタルピー(H):系の内部エネルギーと、系の圧力および体積の数学的積との和
エンタルピー変化(ΔH):化学的または物理的なプロセス中に一定の圧力下で系によって放出または吸収される熱
発熱過程:熱を放出する化学反応や物理的変化
膨張仕事(圧力-体積仕事):系が外部の圧力に対抗して膨張または収縮する際に行われる仕事
熱力学の第一法則:系の内部エネルギーは、系に入ったり出たりする熱流や、系に対してなされた、または系によって行われた仕事のために変化する
熱(q):2つの物体の間での熱エネルギーの移動
熱容量(C):温度を摂氏1度(すなわち1ケルビン)だけ上昇させるのに必要な熱の量を表す物体の示量性
ヘスの法則:もしプロセスがいくつかの段階の合計として表すことができるならば、プロセスのエンタルピー変化はそれぞれの段階のエンタルピー変化の合計に等しい
炭化水素:水素と炭素のみからなる化合物。化石燃料の主要成分
内部エネルギー(U):物質の中に存在するすべての可能な種類のエネルギーの合計
ジュール(J):エネルギーのSI単位。1ジュールは、1秒間に1メートルの速度で移動する1キログラムの質量を持つ物体の運動エネルギー。1 J = 1 kg m²/s² および4.184 J = 1 cal
運動エネルギー:移動する物体のエネルギーをジュールで表したもの。(1/2)mv²に等しい(ここで、m = 質量、v = 速度)
栄養カロリー(大カロリー):食品の消化によって与えられるエネルギーを定量化するために使われる単位。1000 calまたは1 kcalとして定義される
ポテンシャルエネルギー:相対的な位置、組成、または状態に由来する、粒子または粒子の系のエネルギー
比熱容量(c):物質1グラムの温度を摂氏1度(すなわち1ケルビン)だけ上げるのに必要な熱の量を表す物質の示強性
標準燃焼エンタルピー(ΔHc°):標準的な条件下で化合物の1モルが完全に燃焼するときに放出される熱
標準生成エンタルピー(ΔHf°):標準状態の条件下で、最も安定な状態にある元素から1モルの純物質が生成される化学反応のエンタルピー変化
標準状態:熱力学的な性質を報告するための一般的な参照条件として受け入れられている物理的条件のセット。通常は298.15 Kの温度にある、1barの圧力および1モル濃度での溶液
状態関数:系の状態にのみ依存し、その状態に到達するためにとった経路には依存しない性質
周囲:研究対象の系以外のすべての物質
系:研究対象となる化学的または物理的変化を受けている物質の部分
温度:「熱さ」および「冷たさ」の定量的な尺度である物質の示強性
熱エネルギー:原子および分子のランダムな動きに伴う運動エネルギー
熱化学:化学反応や物理的変化の際に吸収されたり放出されたりする熱の量を測定する学問
仕事(w):圧力や体積などの外部の巨視的な変数の変化によるエネルギーの移動、または反対の力に逆らって物質を移動させること
重要な方程式
\(•q = c× m× ΔT = c× m× (T_{\rm final} − T_{\rm initial})\)
\(•ΔU = q + w\)
\(•ΔH_{反応}^° = ∑ n × ΔH_{\rm f} ° (生成物) − ∑ n × ΔH_{\rm f}° (反応物)\)
この章のまとめ
5.1 エネルギーの基本
エネルギーとは、熱を供給したり、(物質を動かすために力を加えて)仕事をしたりする能力のことです。運動エネルギー(KE)は運動のエネルギーであり、ポテンシャルエネルギーは相対的な位置、組成、または状態に起因するエネルギーです。エネルギーがある形態から別の形態に変換されるとき、エネルギーは作り出されることも破壊されることもありません(エネルギーの保存の法則または熱力学の第一法則)。
物質の熱エネルギーは、その構成原子または分子の運動エネルギーによるものです。温度は、平均運動エネルギーの増加に伴って増加する熱さや冷たさを反映した物質の示強性です。熱は、異なる温度の物体間の熱エネルギーの移動です。化学的および物理的なプロセスでは、熱を吸収したり(吸熱)、熱を放出したり(発熱)することがあります。エネルギー、熱、仕事のSI単位はジュール(J)です。
比熱と熱容量は、物質や物体の温度を変化させるのに必要なエネルギーの尺度です。物質によって吸収または放出される熱の量は、物質の種類、質量、およびそれが受ける温度変化に直接依存します。
5.2 熱量測定
熱量測定は、化学的または物理的なプロセスで移動する熱エネルギーの量を測定するために使用されます。これには、プロセス中に発生する温度変化と、系およびその周囲の質量とを注意深く測定する必要があります。これらの測定された量は、既知の数学的関係を使用して、プロセスで生成または消費される熱の量を計算するために使用されます。
熱量計は、その内容物と外部環境との間のエネルギー交換を最小限に抑えるように設計されています。それらの熱量計は、化学の入門学生が使用する単純なコーヒーカップ型の熱量計から、食品のエネルギー含有量を決定するために使用される高度なボンベ熱量計まで、さまざまな種類があります。
5.3 エンタルピー
化学的変化が一定の圧力で行われ、唯一のなされる仕事が膨張または収縮によって引き起こされる場合、その変化についてのqは、エンタルピー変化と呼ばれ、記号ΔHで表されます(または、298 Kでの標準状態の条件下で発生する反応についてはΔH°で表されます)。一方向の反応についてのΔHの値は、反対方向の反応についてのΔHと大きさは等しいですが符号は逆であり、ΔHは反応物と生成物の量に正比例します。標準生成エンタルピーΔHf°は、1bar、298.15 Kで最も安定な状態の元素から1モルの物質を生成することに伴うエンタルピーの変化です。ある反応の反応物と生成物の生成エンタルピーが利用可能な場合、エンタルピー変化はヘスの法則を用いて計算することができます:プロセスがいくつかの段階的なプロセスの合計として書くことができる場合、プロセス全体のエンタルピーの変化は、さまざまな段階のエンタルピーの変化の合計に等しくなります。
練習問題
5.1 エネルギーの基本
1.1本の燃えているマッチと焚き火は同じ温度であるかもしれませんが、あなたは秋の夜に1本の燃えているマッチの周りに座って暖を取ることはないでしょう。なぜですか?
2.自動車の典型的な運転中に起こるいくつかのエネルギー変化を特定した表を作成してください。
3.ある物質の熱容量と比熱の違いを説明してください。
4.以下のものの熱容量を、1度あたりジュールと1度あたりカロリーとで計算してください:
(a)28.4gの水
(b)1.00ozの鉛
5.以下のものの熱容量を、1度あたりジュールと1度あたりカロリーとで計算してください:
(a)45.8gの窒素気体
(b)アルミニウム金属1.00ポンド
6.比熱が0.449J/g °Cで75.0gの鉄塊の温度を、25°Cから融解温度1535°Cまで上昇させるためには、どれだけの熱(ジュールとカロリーで)を加えなければならないですか?
7.28.4g(1oz)の角氷を-23.0°Cから-1.0°Cに加熱するのに必要な熱の量は、ジュールとカロリーでいくらですか?
8.275gの水の温度は、36.5kJの熱を加えると、どれだけ上昇するでしょうか?
9.もし485gの液体の水に14.5kJの熱を加えたならば、その温度はどれだけ上昇するでしょうか?
10.ある未知の物質の一片は、重さが44.7gであり、その温度を23.2°Cから89.6°Cに上昇させるには2110Jを必要としました。
(a)その物質の比熱は何ですか?
(b)もしそれが表5.1にある物質の1つである場合、その物質の正体である可能性が高いものは何ですか?
11.ある未知の固体の物質の一片は、重さが437.2gであり、その温度を19.3°Cから68.9°Cに上昇させるのに8460Jを必要としました。
(a)その物質の比熱は何ですか?
(b)もしそれが表5.1にある物質の1つである場合、その物質の正体である可能性が高いものは何ですか?
12.アルミニウム製のやかんの重さは1.05kgです。
(a)このやかんの熱容量は何ですか?
(b)このやかんの温度を23.0°Cから99.0°Cに上げるのに必要な熱の量は何ですか?
(c)このやかんの中に1.25 Lの水(密度0.997 g/mL、比熱4.184 J/g °C)が含まれている場合、このやかんを23.0 °Cから99.0 °Cに加熱するのに必要な熱の量は何ですか?
13.ほとんどの人は、ウォーターベッドの水温が約85°Fに維持されていない限り、快適でないと感じます。加熱しない限り、892 Lの水を含むウォーターベッドは、24時間で85 °Fから72 °Fに冷却されます。ベッドが冷えないようにするために24時間に必要な電気エネルギーの量をkWhで見積もってください。1キロワット時 (kWh) = 3.6×10⁶J であることに注意し、水の密度を 1.0 g/mL (温度に依存しない)と仮定してください。あなたは他にどのような仮定をしましたか? それらは計算結果にどのような影響を与えましたか(すなわち、それらは「正」または「負」の誤差を生じさせる可能性がありましたか)?
5.2 熱量測定
14.室温の水500mLが入ったボトルと、同じ温度の水2Lが入ったボトルを冷蔵庫に入れました。30分後、500mLのボトルの水は冷蔵庫の温度まで冷えていました。1時間後、2Lの水が同じ温度まで冷えていました。どちらの水の試料が最も多くの熱を失ったかという質問に対して、ある学生は、両方のボトルは同じ温度で始まり、同じ温度で終わったので、どちらのボトルも同じ量の熱を失ったと答えました。2人目の学生は、2Lの水のボトルの方が水の量が多いので、より多くの熱を失ったと考えました。3人目の学生は、500mlの水のボトルの方が早く冷えたので、より多くの熱を失ったと考えました。4人目の学生は、水の初期温度と最終温度を知らないので、答えることはできないと考えました。これらの答えのうち、どれが正しいかを示し、他のそれぞれの答えの誤りを説明してください。
15.例題5.5の反応で測定した熱の量は、もしあなたがコーヒーカップ型の熱量計よりも絶縁性の悪い熱量計を使用した場合、大きくなるでしょうか、小さくなるでしょうか、変わらないでしょうか?あなたの答えを説明してください。
16.例題5.6の溶解によって吸収された熱の量は、もし実験者がコーヒーカップ型の熱量計よりも絶縁性の悪い熱量計を使用した場合、大きくなるでしょうか、小さくなるでしょうか、変わらないでしょうか?あなたの答えを説明してください。
17.例題5.6の溶解によって吸収された熱の量は、熱量計の熱容量を考慮に入れた場合、大きくなるでしょうか、小さくなるでしょうか、変わらないでしょうか?あなたの答えを説明してください。
18.95°Cのコーヒー180 mL(約6oz)と混ぜ合わせて、結果として生じた混合物の温度が60°Cになるようにするには、23°Cの水(密度1.00g/mL)を何ミリリットル混ぜ合わせなければならないでしょうか?コーヒーと水は同じ密度で同じ比熱を持つと仮定してください。
19.一杯の95°Cのコーヒー(180g)の中に、25°Cで45gの銀製スプーン(比熱0.24J/g°C)を入れて2つが同じ温度になるようにしたとき、コーヒーの温度はどれだけ下がるでしょうか?コーヒーの密度と比熱は水と同じであると仮定してください。
20.24°Cで45gのアルミニウム製スプーン(比熱0.88J/g °C)を85°Cのコーヒー180mL(180g)に入れ、両者の温度が同じになるようにしました。
(a)両者の温度が等しくなったときの最終温度は何ですか?コーヒーの比熱は水と同じであると仮定してください。
(b)この問題を初めて解いた学生は、88°Cという答えを出しました。これが明らかに不正解である理由を説明してください。
21.自動車の高温のエンジンから出てくる際の冷却水の温度は240°Fです。それがラジエーターを通過した後の温度は175°Fです。比熱が4.184 J/g °Cの水1ガロンによってエンジンから周囲に伝わる熱の量を計算してください。
22.80.0°Cで70.0gの金属片を、図5.12に示されるような熱量計の中に含まれる22.0°Cの水100gの中に入れます。金属と水は24.6°Cで同じ温度になりました。この金属はどれだけの熱を水に与えましたか?この金属の比熱は何ですか?
23.ある反応で1.506 kJの熱が発生します。その熱が図5.12に示されるような熱量計の中にある30.0 gの水(最初は26.5 °C)に捕らえられたとすると、その結果の水の温度は何ですか?
24.0.500gのKCl試料を熱量計(図5.12)の中の50.0gの水に加えます。結果として生じる溶液の比熱が4.18 J/g °Cであると仮定して、もし温度が1.05°Cだけ下がったならば、KClの溶解に関与するおおよその熱の量は何ですか?反応は発熱性ですか、それとも吸熱性ですか?
25.3.0gのCaCl₂(s)を熱量計(図5.12)の中の150.0gの水(22.4°C)に溶解させると、温度は25.8°Cに上昇しました。結果として生じる溶液の比熱が4.18 J/g °Cであると仮定して、溶解に関与するおおよその熱の量は何ですか?反応は発熱性ですか、それとも吸熱性ですか?
26.熱量計の中において、24.1 °Cで0.200MのNaCl(aq)50.0 gを、24.1 °Cで0.100MのAgNO₃(aq)100.0 gに加えると、AgCl(s)が生成されて温度が25.2 °Cに上昇しました。溶液と生成物の比熱が4.20 J/g °Cであると仮定して、生成された熱のおおよその量をジュールで計算してください。
27.熱量計に入っている100gの水の中で、1.52gのNH₄SCN溶液に3.15gのBa(OH)₂·8H₂Oを加えると、温度が3.1°C低下しました。溶液と生成物の比熱が4.20 J/g °Cであると仮定して、以下の反応式で表される反応によって吸収された熱のおおよその量を計算してください:
Ba(OH)₂·8H₂O(s) + 2NH₄SCN(aq) ⟶ Ba(SCN)₂(aq) + 2NH₃(aq) + 10H₂O(l)
28.例題5.5で記述した50 mLの酸と50 mLの塩基の反応では、溶液の温度が6.9°Cだけ上昇しました。同じ熱量計の中で同じ22.0°Cの温度から始めて100mLの酸と100mLの塩基を使った場合、どれだけの温度が上がるでしょうか?あなたの答えを説明してください。
29.例題5.6における3.21gのNH₄NO₃を同じ条件下で 100.0 g の水に溶かした場合、温度はどれだけ変化するでしょうか?あなたの答えを説明してください。
30.果物によく含まれる糖類であるフルクトースC₆H₁₂O₆(s)1.0 gをボンベ熱量計の中で酸素で燃焼させると、熱量計の温度は1.58 °Cだけ上昇しました。熱量計とその内容物の熱容量が9.90 kJ/°Cであるとすると、この燃焼のqは何ですか?
31.トリニトロトルエン(TNT)C₇H₅N₂O₆の試料0.740gをボンベ熱量計の中で燃焼させると、温度が23.4°Cから26.9°Cに上昇しました。熱量計の熱容量は 534 J/°Cで、675 mL の水が入っています。TNT試料の燃焼によってどれだけの熱が発生しましたか?
32.発電の1つの方法は、石炭を燃やして水を加熱し、蒸気を発生させて発電機を駆動させることです。この種の発電プラントにおいて石炭を燃焼炉に投入する速度を決定するには、ボンベ熱量計を用いて石炭1トンあたりの燃焼熱を決定しなければなりません。1.00gの石炭をボンベ熱量計(図5.17)の中で燃焼させると、温度は1.48°Cだけ上昇しました。熱量計の熱容量が21.6kJ/°Cの場合、石炭1トン(2.000×10³ポンド)の燃焼によって生じる熱を決定してください。
33.1日2000大カロリーの食生活を送る人に推奨されている脂肪の量は65gです。脂肪の平均大カロリー数が9.1大カロリー/gである場合、この食生活において、その脂肪の量によって供給されるであろうカロリーの割合は何%ですか?
34.炭水化物のスクロース(一般的な砂糖)小さじ1杯には16大カロリー(16kcal)が含まれています。炭水化物の平均大カロリー数が4.1大カロリー/gである場合、スクロース小さじ1杯の質量は何ですか?
35.炭水化物の平均大カロリー数が4.1大カロリー/gである場合、1缶あたり1大カロリー未満を含むダイエットソーダの6オンスに含まれる炭水化物の最大質量は何ですか?
36.高級アイスクリーム1パイントには1100大カロリーが含まれています。脂肪の平均大カロリー数が9.1大カロリー/gである場合、余分な1.1×10³大カロリーを蓄えるために、体内で何グラムおよび何ポンドの質量の脂肪が生産されなければなりませんか?
37.朝食用シリアル一皿には、3gのタンパク質、18gの炭水化物、6gの脂肪が含まれています。脂肪の平均大カロリー数が9.1大カロリー/g、炭水化物の平均大カロリー数が4.1大カロリー/g、タンパク質の平均大カロリー数が4.1大カロリー/gである場合、このシリアル一皿の大カロリー含有量は何ですか?
38.1ドルあたりのキロジュールで最も安価なエネルギー源はどちらですか?:32オンスの重さで4.23ドルの朝食用シリアルの一箱、または0.45ドルのイソオクタン(密度0.6919 g/mL)1リットル。シリアルの栄養価と、標準的な条件下でのイソオクタンの燃焼によって生じる熱を比較してください。1.0オンスのシリアル一皿は130大カロリーを提供します。
5.3 エンタルピー
39.例題5.5で測定した熱が、以下の反応式で表される発熱反応のエンタルピー変化とどのように異なるかを説明してください:
HCl(aq) + NaOH(aq) ⟶ NaCl(aq) + H₂O(l)
40.例題5.5の学習内容の確認のセクションのデータを使用して、以下の反応についてのAgNO₃(aq)のΔHをkJ/molで計算してください:
NaCl(aq) + AgNO₃(aq) ⟶ AgCl(s) + NaNO₃(aq)
41.例題5.6で記述された条件下で、NH₄NO₃の1モルあたりの溶液のエンタルピー(溶解についてのΔH)を計算してください。
42.以下の反応式で表される反応のΔHを計算してください。(ヒント: 前の練習問題で計算した反応の吸熱量のおおよその値を使用してください。)
Ba(OH)₂·8H₂O(s) + 2NH₄SCN(aq) ⟶ Ba(SCN)₂(aq) + 2NH₃(aq) + 10H₂O(l)
43.CaCl₂の1モルあたりの溶液のエンタルピー(溶解のΔH)を計算してください(練習問題5.25参照)。
44.酸素アセチレントーチ(図5.7)で使用されているガスは基本的に純粋なアセチレンですが、このようなトーチで1モルのアセチレンを燃焼させることによって生じる熱は、表5.2に記載されているアセチレンの燃焼のエンタルピーと等しくない可能性があります。表のデータが報告されている条件を考慮して、その説明を提案してください。
45.標準状態の条件下で4.00モルのアセチレンを燃焼させることによってどれだけの熱が発生しますか?
46.標準状態の条件下で125gのメタノールを燃焼させることによってどれだけの熱が発生しますか?
47.標準状態の条件下で100kJの熱を発生させるためには、何モルのイソオクタンを燃焼させなければならないですか?
48.標準状態の条件下で175kJの熱を発生させるためには、どれだけの質量の一酸化炭素を燃焼させなければならないですか?
49.2.50gのメタンが酸素中で燃焼すると、125kJの熱が発生します。これらの条件下でのメタンの1モルあたりの燃焼エンタルピーは何ですか?
50.0.250 MのHCl(濃度1.00 g/mL)100 mLと0.150 MのNaOH(濃度1.00 g/mL)200 mLを混合したとき、どれだけの熱が発生するでしょうか?
HCl(aq) + NaOH(aq) ⟶ NaCl(aq) + H₂O(l) ΔH° = −58kJ
両方の溶液が同じ温度で、生成物の熱容量が4.19 J/g °Cの場合、温度はどれだけ上昇するでしょうか?計算ではどのような仮定をしましたか?
51.0.562gの炭素試料をボンベ熱量計の中で酸素で燃焼させて、二酸化炭素を生成しました。反応物と生成物の両方が標準状態の条件下にあると仮定し、また、放出される熱は黒鉛の燃焼のエンタルピーに正比例すると仮定します。熱量計の温度は 26.74 °Cから 27.93 °Cに上昇しました。熱量計の熱容量とその内容物は何ですか?
52.クロロフルオロカーボン(フロン類)が導入される前は、家庭用冷蔵庫には二酸化硫黄(蒸発のエンタルピー、6.00kcal/mol)が使用されていました。1.00kgのCCl₂F₂(蒸発のエンタルピーは17.4kJ/mol)を蒸発させるのと同じくらいの熱を除去するには、どれだけの質量のSO₂を蒸発させなければならないですか?SO₂とCCl₂F₂の蒸発反応は、それぞれSO₂(l)⟶ SO₂(g)とCCl₂F(l)⟶ CCl₂F₂(g)です。
53.住宅はラジエーターを通して温水を汲み上げることで暖房されることがあります。100gの水蒸気を110°Cから100°Cに冷却したときに提供される熱と同じ量の熱を提供するためには、どれだけの質量の水を95.0°Cから35.0°Cに冷却する必要がありますか?
54.表5.2の燃焼のエンタルピーのうち、標準生成エンタルピーでもあるものはどれですか?
55.H₂O(g)の標準生成エンタルピーは、2H₂(g)+O₂(g)⟶ 2H₂O(g)の反応のΔH°と異なるでしょうか?
56.ジョゼフ・プリーストリーは1774年に、レンズを通して集光した太陽光で赤色の酸化水銀(II)を加熱することによって酸素を調製しました。標準的な条件下で、正確に1モルの赤色のHgO(s)をHg(l)とO₂(g)に分解するためにはどれだけの熱が必要でしょうか?
57.標準状態の条件で正確に1モルのマンガン(Mn)を燃焼させてMn₃O₄(s)を生成するとき、何キロジュールの熱が放出されますか?
58.標準状態の条件で正確に1モルの鉄(Fe)を燃焼させてFe₂O₃(s)を生成するとき、何キロジュールの熱が放出されますか?
59.硝酸水溶液の商業的な生産では、以下のような一連の反応が起こります:
4NH₃(g) + 5O₂(g) ⟶ 4NO(g) + 6H₂O(l) ΔH = −907kJ
2NO(g) + O₂(g) ⟶ 2NO₂(g) ΔH = −113kJ
3NO₂ + H₂O(l) ⟶ 2HNO₃(aq) + NO(g) ΔH = −139kJ
このプロセスによって1モルの硝酸水溶液を生成するための総エネルギー変化を決定してください。
60.黒鉛もダイヤモンドも燃えます。
C(s,ダイヤモンド) + O₂(g) ⟶ CO₂(g)
黒鉛からダイヤモンドへの変換は、以下の通りです。
C(s,黒鉛) ⟶ C(s,ダイヤモンド) ΔH° = 1.90 kJ
黒鉛の燃焼とダイヤモンドの燃焼のうち、どちらがより多くの熱を発生させますか?
61.付録Gの生成のモル熱から、水1モルを蒸発させるのに必要な熱の量を求めてください:H₂O(l) ⟶ H₂O(g)
62.相変化OsO₄(s) ⟶ OsO₄(g) ΔH = 56.4 kJであるとき、以下のうちどちらがより多くの熱を生成するでしょうか?
Os(s) + 2O₂(g) ⟶ OsO₄(s)
または
Os(s) + 2O₂(g) ⟶ OsO₄(g)
63.以下の情報:
\({\rm Sb\ (s) +\frac{3}{2} Cl_2\ (g) ⟶ SbCl_3\ (s)} \hspace{20pt} ΔH° = {\rm −314\ kJ}\)
\({\rm SbCl_3\ (s) + Cl_2\ (g) ⟶ SbCl_5\ (s)} \hspace{20pt} ΔH° = {\rm −80\ kJ}\)
から、以下のプロセスのΔH°を計算してください。
\(\rm Sb\ (s) +\frac{5}{2} Cl_2\ (g) ⟶ SbCl_5\ (s)\)
64.以下の情報:
\({\rm Zn\ (s) + S\ (s) ⟶ ZnS\ (s)} \hspace{20pt} ΔH° = {\rm −206.0\ kJ}\)
\({\rm ZnS\ (s) + 2O_2\ (g) ⟶ ZnSO_4\ (s)} \hspace{20pt} ΔH° = {\rm −776.8\ kJ}\)
から、以下のプロセスのΔH°を計算してください。
\(\rm Zn\ (s) + S\ (s) + 2O_2\ (g)⟶ ZnSO_4\ (s)\)
65.以下の情報:
\({\rm Hg\ (l) + Cl_2\ (g) ⟶ HgCl_2\ (s)} \hspace{20pt} ΔH = {\rm −224\ kJ}\)
\({\rm Hg\ (l) + HgCl_2\ (s) ⟶ Hg_2 Cl_2\ (s)} \hspace{20pt} ΔH = {\rm −41.2\ kJ}\)
から、以下のプロセスのΔHを計算してください。
\(\rm Hg_2 Cl_2\ (s) ⟶ 2Hg\ (l) + Cl_2\ (g)\)
66.以下の情報:
\({\rm Co\ (s) +\frac{1}{2} O_2\ (g) ⟶ CoO\ (s)} \hspace{20pt} ΔH° = {\rm −237.9\ kJ}\)
\({\rm 3CoO\ (s) +\frac{1}{2} O_2\ (g) ⟶ Co_3 O_4\ (s)} \hspace{20pt} ΔH° = {\rm −177.5\ kJ}\)
から、以下のプロセスのΔH°を計算してください。
\(\rm Co_3 O_4\ (s) ⟶ 3Co\ (s) + 2O_2\ (g)\)
67.以下のデータからNO(g)の標準生成モルエンタルピーを計算してください:
N₂(g) + 2O₂ ⟶ 2NO₂(g) ΔH° = 66.4 kJ
2NO(g) + O₂ ⟶ 2NO₂(g) ΔH° = −114.1 kJ
68.付録Gのデータを用いて、以下のそれぞれの反応の標準エンタルピー変化を計算してください:
(a)N₂(g) + O₂(g) ⟶ 2NO(g)
(b)Si(s) + 2Cl₂(g) ⟶ SiCl₄(g)
(c)Fe₂O₃(s) + 3H₂(g) ⟶ 2Fe(s) + 3H₂O(l)
(d)2LiOH(s) + CO₂(g) ⟶ Li₂CO₃(s) + H₂O(g)
69.付録Gのデータを用いて、以下のそれぞれの反応の標準エンタルピー変化を計算してください:
(a)Si(s) + 2F₂(g) ⟶ SiF₄(g)
(b)2C(s) + 2H₂(g) + O₂(g) ⟶ CH₃CO₂H(l)
(c)CH₄(g) + N₂(g) ⟶ HCN(g) + NH₃(g)
(d)CS₂(g) + 3Cl₂(g) ⟶ CCl₄(g) + S₂Cl₂(g)
70.金属の試料を調製するために、以下の反応を用いることができます。それぞれについて、標準状態の条件下でのエンタルピー変化を求めてください。
(a)2Ag₂O(s) ⟶ 4Ag(s) + O₂(g)
(b)SnO(s) + CO(g) ⟶ Sn(s) + CO₂(g)
(c)Cr₂O₃(s) + 3H₂(g) ⟶ 2Cr(s) + 3H₂O(l)
(d)2Al(s) + Fe₂O₃(s) ⟶ Al₂O₃(s) + 2Fe(s)
71.さまざまな宇宙船の制御ジェットの推力を得るために過酸化水素(H₂O₂)の分解が使用されています。付録Gのデータを用いて、標準的な条件下で正確に1モルのH₂O₂を分解したときに生じる熱量を求めてください。
2H₂O₂(l) ⟶ 2H₂O(g) + O₂(g)
72.プロパンC₃H₈(g)の燃焼によるH₂O(g)とCO₂(g)の生成のエンタルピーを計算してください。プロパンの生成のエンタルピーは-104 kJ/molです。
73.ブタンC₄H₁₀(g)の燃焼によるH₂O(g)とCO₂(g)の生成のエンタルピーを計算してください。ブタンの生成のエンタルピーは-126 kJ/molです。
74.プロパンとブタンはどちらも気体状の燃料として使用されています。燃やしたとき、グラムあたりの熱を多く発生させるのはどちらの化合物ですか?
75.白色顔料TiO₂は四塩化チタンTiCl₄と気相中の水蒸気との反応によって生成します:
TiCl₄(g) + 2H₂O(g) ⟶ TiO₂(s) + 4HCl(g)
標準状態の条件下で、正確に1モルのTiO₂(s)が生成されるとき、どれだけの熱が発生しますか?
76.H₂とCOの混合物である水性ガスは、水蒸気と赤熱コークス(本質的には純粋な炭素です)の反応によって生成される重要な工業用燃料です:C(s) + H₂O(g) ⟶ CO(g) + H₂(g)
(a)コークスが黒鉛と同じ生成エンタルピーを持つと仮定して、この反応のΔH°を計算してください。
(b)ガソリンに代わる可能性を持つ液体燃料であるメタノールは、適切な触媒が存在する高温高圧下で、水性ガスと追加の水素から生成することができます:2H₂(g) + CO(g) ⟶ CH₃OH(g)
この反応の条件下では、メタノールは気体として生成します。この反応についてのΔH°と、気体のメタノールから液体のメタノールへの凝縮についてのΔH°を計算してください。
(c)液体メタノール1モルがH₂O(g)とCO₂(g)へと燃焼するときの熱を計算してください。
77.自動車の黎明期には、夜間の照明のためにアセチレン(C₂H₂)を燃やしていました。現在では自動車のヘッドライトとしては使われていませんが、一部の洞窟探検家はまだアセチレンを光源として使用しています。アセチレンは、水とカルシウムカーバイドCaC₂との反応によってランプ内で生成されます:
CaC₂(s) + 2H₂O(l) ⟶ Ca(OH)₂(s) + C₂H₂(g)
この反応の標準エンタルピーを計算してください。CaC₂のΔHf°は-15.14 kcal/molです。
78.表5.2のデータから、標準的な条件下で燃焼させたとき、1グラムあたりで発生させる熱の量が最も大きい燃料は以下のうちどれであるかを決定してください:CO(g)、CH₄(g)、またはC₂H₂(g)。
79.無煙炭の燃焼のエンタルピーは平均で-35 kJ/g、ガソリンの燃焼のエンタルピーは1.28×10⁵kJ/galです。1.0ガロンのガソリンから得られる熱量と同じ量の熱を、何キログラムの石炭から得ることができるでしょうか?ガソリンの密度が0.692g/mL(イソオクタンの密度と同じ)であると仮定してください。
80.エタノールC₂H₅OHは、特にブラジルで、自動車用燃料として使用されています。
(a)エタノールをCO₂(g)とH₂O(g)へと燃焼することについてのバランスの取れた反応式を書き、付録Gのデータを用いて、1モルのエタノールの燃焼のエンタルピーを計算してください。
(b)エタノールの密度は 0.7893 g/mL です。正確に1 Lであるエタノールの燃焼のエンタルピーを計算してください。
(c)自動車の走行距離が燃料の燃焼の熱に正比例すると仮定して、1Lのガソリンを使用した場合に予想される自動車の走行距離が、1Lのエタノールを使用した場合に予想される自動車の走行距離よりもどれだけ長くなるかを計算してください。ガソリンはn-オクタンC₈H₁₈の燃焼熱と密度(ΔHf° = -208.4kJ/mol、密度 = 0.7025 g/mL)を持っていると仮定してください。
81.酸素と反応し、ロケット燃料の可能性があるとみなされている物質に、ジボラン[B₂H₆、B₂O₃(s)とH₂O(g)を生成します]、メタン[CH₄、CO₂(g)とH₂O(g)を生成します]、ヒドラジン[N₂H₄、N₂(g)とH₂O(g)を生成します]などがあります。それぞれの物質1.00gと酸素との反応によって放出される熱に基づくと、ロケット燃料として最も可能性がある化合物はどれですか?B₂H₆(g)、CH₄(g)、N₂H₄(l)のΔHf°は付録Gに記載されています。
82.金属クロム1.25gが標準的な条件下で酸素気体と反応したとき、どれだけの熱が発生しますか?
83.石油の分留からの副生成物であるエチレン(C₂H₄)は、最も多く商業的に生産される50種類の化合物の中で4番目に位置しています。合成エタノールの約80%は、適切な触媒の存在下での水とエチレンとの反応から製造されています:C₂H₄(g) + H₂O(g) ⟶ C₂H₅OH(l) 付録Gの表のデータを用いて、この反応のΔH°を計算してください。
84.糖のグルコース(C₆H₁₂O₆)の酸化は、以下の反応式で表されます:
C₆H₁₂O₆(s) + 6O₂(g) ⟶ 6CO₂(g) + 6H₂O(l) ΔH = −2816kJ
グルコースの代謝では、グルコースが体内の一連の段階で酸素と反応しますが、同じ生成物が生じます。
(a)1.0gのグルコースの代謝によって、キロジュール単位でどれだけの熱が生成されますか?
(b)1.0gのグルコースの代謝によって、大カロリーはどれだけ生成されますか?
85.プロパン(C₃H₈)は、燃料として一般的に使用されている炭化水素です。
(a)気体のプロパンの完全燃焼についてのバランスの取れた反応式を書いてください。
(b)25.0グラムのプロパンを完全に燃焼させるために必要な空気の体積(25°C、1.00気圧)を計算してください。空気は体積比でO₂が21.0%であると仮定してください。(ヒント:私たちは、この計算を行う方法を後の気体に関する章で見ていきます。今は、25 °C、1.00atmで1.00 Lの空気には1リットルあたり0.275 gのO₂が含まれているという情報を使用してください。)
(c)プロパンの燃焼熱は-2219.2 kJ/molです。H₂O(l)のΔHf°= -285.8 kJ/molおよびCO₂(g)のΔHf°= -393.5 kJ/molである場合、プロパンの生成熱ΔHf°を計算してください。
(d)25.0 グラムのプロパンを燃焼させたときに放出された熱のすべてが 4.00 キログラムの水に移動したと仮定して、水の温度の上昇を計算してください。
86.ウィスコンシン州シボイガンでは、最近の冬のある一か月の間に一軒の小さな家を暖めるためには、89%の効率を持つ天然ガス炉によって生成された3500kWhの熱を得る必要がありました(ガス炉の効率とは、燃焼によって生成された熱のうち家の中に移動する割合のことです)。
(a)天然ガスが純粋なメタンであると仮定して、家を暖めるのに必要な天然ガスの体積を立方フィート単位で求めてください。天然ガスの平均温度は56°Fです。この温度と1atmの圧力では、天然ガスの密度は0.681g/Lです。
(b)使用した天然ガスを置き換えるためには、何ガロンのLPG(液化石油ガス)が必要でしょうか?LPGは液体プロパン[C₃H₈:密度0.5318 g/mL、CO₂(g)とH₂O(l)を生成する燃焼エンタルピー2219 kJ/mol]であると仮定し、LPGを燃焼させるために使われる炉がガス炉と同じ効率であると仮定してください。
(c)家を暖めるために使用したメタンの燃焼によってどれだけの質量の二酸化炭素が生成されましたか?
(d)家を暖めるために使用したメタンの燃焼によってどれだけの質量の水が生成されましたか?
(e)家を暖めるために使用したメタンの燃焼に酸素を供給するためには、どれだけの体積の空気が必要ですか?空気には質量比で23%の酸素が含まれています。この一か月の間の空気の平均密度は1.22g/Lでした。
(f)家を暖めるために必要な熱を供給するためには、何キロワット時(1kWh = 3.6 × 10⁶J)の電気が必要でしょうか?電気は家の中で熱を作り出すのに100%の効率であることに注意してください。
(g)電気は家の中で熱を作り出す際には100%の効率ですが、電気の発電と配電は100%の効率というわけではありません。石炭火力発電所で発電される電気の発電および配電効率は約40%です。ある種類の石炭は、燃焼時に1ポンドあたり2.26kWhの電力を供給します。発電および配電効率が40%である場合、家を暖めるために必要な電気エネルギーを得るためには、この石炭は何キログラムの質量が必要でしょうか?
解答のヒント
1.マッチでも焚き火でも、1gの燃える木の温度はほぼ同じです。これは示強性であり、材料(木材)に依存します。しかしながら、発生する熱の全体的な量は材料の量に依存します。これは示量性です。焚き火の中にある木の量は1本のマッチに比べて量が多く、発生する熱の総量も多いので、私たちは焚き火を囲んで座って暖を取ることができますが、1本のマッチは寒さをしのげるほどの熱を与えることはないでしょう。
3.熱容量とは、物質の塊の温度を1度だけ上昇させるのに必要な熱のことを指します。比熱とは、物質1グラムの温度を1度だけ上昇させるのに必要な熱のことを指します。したがって、熱容量は示量性であり、比熱は示強性です。
5.(a)47.6 J/°C、11.38 cal/°C、(b)407 J/°C、97.3 cal/°C
7.1310 J、313 cal
9.7.15 °C
11.(a)0.390 J/g °C、(b)銅が可能性のある候補です。
13.私たちは、水の密度が1.0 g/cm³(1 g/mL)であると仮定し、水を85 °Fで維持するためには水を72 °Fから85 °Fに加熱するのと同じだけのエネルギーが必要であると仮定します。また、水だけが加熱されると仮定します。必要なエネルギー = 7.47 kWh
15.小さくなります。より多くの熱がコーヒーカップと環境に失われるので、水のΔTはより小さくなり、計算されたqはより小さくなるでしょう。
17.大きくなります。熱量計の熱容量を考慮に入れると、熱量計から溶液に移る熱エネルギーが補償されるからです。このアプローチでは、熱量計自体を、溶液とともに「周囲」として含めることになります。: qrxn = −(q溶液 + q熱量計)。q溶液とq熱量計の両方が負の値であるため、後者を含めることで溶解の熱の値は大きくなるでしょう。
19.コーヒーの温度は1度下がるでしょう。
21.5.7 × 10²kJ
23.38.5 °C
25.−2.2 kJ。生成された熱は、反応が発熱性であることを示しています。
27.1.4 kJ
29.22.6°C。溶液の質量および熱容量は水の質量および熱容量とほぼ等しいので、水の量が2倍になると温度変化が半分になります。
31.11.7 kJ
33.30%
35.0.24 g
37.1.4 × 10²大カロリー
39.示された反応のエンタルピー変化は、正確に1 molのHCLと1 molのNaOHのためのものです。例題の熱は、0.0500 molのHClと0.0500 molのNaOHによって生成されています。
41.25 kJ/mol
43.81 kJ/mol
45.5204.4 kJ
47.1.83 × 10⁻²mol
49.–802 kJ/mol
51.15.5 kJ/ºC
53.7.43 g
55.はい
57.459.6 kJ
59.−494 kJ/mol
61.44.01 kJ/mol
63.−394 kJ
65.265 kJ
67.90.3 kJ/mol
69.(a)−1615.0 kJ/mol、(b)−484.3 kJ/mol、(c)164.2 kJ、(d)−232.1 kJ
71.−54.04 kJ/mol
73.−2660 kJ/mol
75.67.1 kJ
77.−122.8 kJ
79.3.7 kg
81.最も良いロケット燃料は最も熱を発するものであると仮定した場合、B₂H₆が最有力候補となります。
83.−88.2 kJ
85.(a)C₃H₈(g) + 5O₂(g) ⟶ 3CO₂(g) + 4H₂O(l)、(b)330 L、(c)−104.5 kJ/mol、(d)75.4 °C
[1] US Energy Information Administration, Primary Energy Consumption by Source and Sector, 2012, http://www.eia.gov/totalenergy/data/monthly/pdf/flow/css_2012_energy.pdf. Data derived from US Energy Information Administration, Monthly Energy Review (January 2014).
[2] Francis D. Reardon et al. “The Snellen human calorimeter revisited, re-engineered and upgraded: Design and performance characteristics.” Medical and Biological Engineering and Computing 8 (2006)721–28, http://link.springer.com/article/10.1007/s11517-006-0086-5.
[3] 藻類燃料の詳細については、http://www.theguardian.com/environment/2010/feb/13/algae-solve-pentagon-fuel-problemを参照。
この訳文は元の本のCreative Commons BY 4.0ライセンスに従って同ライセンスにて公開します。問題がありましたら、可能な限り早く対応いたしますので、ご連絡ください。また、誤訳・不適切な表現等ありましたらご指摘ください。この本は、https://openstax.org/details/books/chemistry-2eで無料でダウンロードできます。